基于多重网格的模拟退火算法

陶庆云



基于多重网格的模拟退火算法

陶庆云*

(湖南文理学院 数学与计算科学学院, 湖南 常德, 415000)

为了提高模拟退火算法的收敛速度, 提出了一种基于多重网格的模拟退火算法(SAM), 用于求解高维函数优化问题, 并分析了其收敛性. 13个著名的测试函数对SAM算法进行数值实验, 结果表明SAM算法具有良好的搜索能力和收敛速度.

模拟退火算法; 多重网格法; 函数优化问题

模拟退火算法(Simulated Annealing)[1]在1982年由Kirkpatrick等人首次提出, 是一种基于Monte Carlo迭代求解法的启发式随机搜索算法. 它能够有效的避免局部搜索算法易陷入局部最优的通病, 是一种和遗传算法一样被广泛应用的优秀全局搜索算法. 然而理论研究表明模拟退火算法实现全局收敛的时间性能很差[2], 大量实验也表明在求解高维函数优化问题时其搜索能力非常有限.

多重网格法[3]被认为是求解偏微分方程组收敛速度最快的数值方法之一. 它由多层粗细不同的网格组成, 在粗网格上, 数值算法快速收敛, 但解的质量较差, 在细网格上算法收敛到高精度的解, 但收敛速度较慢. 粗细网格的结合, 使得数值算法能以较短的时间收敛到高精度的解. 已有不少研究者将多重网格法与智能算法相结合用于求解复杂函数优化问题[4—6]等, 文献[6]详细讨论了多重网格法与演化算法结合的应用模式及其收敛性. 本文提出了一种基于多重网格的模拟退火算法, 以文献[6]中13个著名的测试函数为例对SAM算法进行数值实验, 其中函数的变量个数均为30, 结果表明多重网格法能有效提高模拟退火算法的搜索能力和收敛速度.

1 多重网格法

考虑函数优化问题:

2 基于多重网格的模拟退火算法

下面给出基于多重网格的模拟退火算法流程:

Begin:

Initialize;

Restriction();

While not termination condition;

For2 i=0 to Markov chain length L do

Generate a new solution;

Evaluate new solution, calculate the difference df;

If df>0 or (df<0 and exp(-df/T)>rand(0,1) )

Accept the new solution;

Else

Accept the old one;

For3 three components of variable do

Simulated annealing;

End of for3

End of for2

End of while

End of for1

End

下面分析SAM算法的收敛性: 首先, 算法的搜索始终保持在网格上, 从一个初始状态开始后, 每一步状态转移都是在当前状态的临域中随机产生新状态, 然后以一定概率接受, 接受概率仅依赖于新状态和当前状态, 并由温度加以控制. 因此, SAM算法对应一个有限状态马氏链. 在每一温度下, 算法充分遍历, 计算马氏链的变化直至平稳分布, 从而SAM算法属于时齐算法. 这说明在每层网格上SAM算法都以概率1收敛到全局最优解.

3 数值实例

表1 算法运行结果

4 结论

本文提出了一种基于多重网格的模拟退火算法, 实验结果证明SAM算法比传统的SA算法搜索能力显著提高, 参见文献[2]中SA算法结果. 与文献[6]中结果具有可比性. 这说明多重网格法能有效提高模拟退火算法的搜索能力和收敛速度. 值得注意的是多重网格法并非一种独立的搜索算法, 它具有很多种形式[9], 应该与智能算法或数值算法完美结合才能更好的为人们所用.

附录: 测试函数

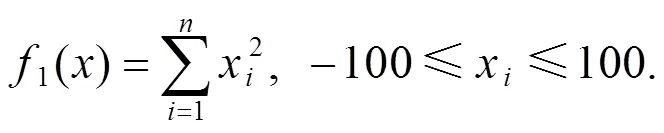
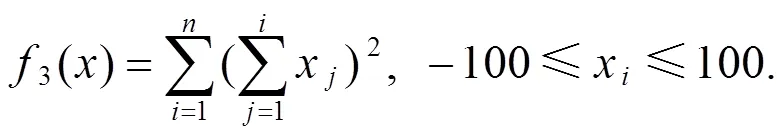
[1] 康立山. 非数值并行算法–模拟退火算法[M]. 北京: 科学出版社, 1998.

[2] 王凌. 智能优化算法及其应用[M]. 北京: 清华大学出版社, 2010.

[3] Hackbusch W. Multigrid Methods and Applications[M]. Berlin: Springer-Verlag, 1985.

[4] Brandt A, Ron D. Multigrid solvers and multilevel optimization strategies[M].Boston: Kluwer Academic Publishers, 2003: 1—69.

[5] Gelman E, Mandel J. Multilevel algorithms for optimization problems[J]. Math Progr Ser B, 1990, 48: 1—18.

[6] He Jun, Kang Lishan. A mixed strategy of combining evolutionary algorithms with multigrid methods[J]. International Journal of Computer Mathematics, 2009, 86(5): 837—849.

[7] Dong H, He J, Huang H, et al. Evolutionary programming using a mixed mutation strategy[J]. Inform Sci, 2007, 177(1): 312—327.

[8] Lee C Y, Yao X. Evolutionary programming using mutations based on the Levy probability distribution[J]. IEEE Trans Evol Comput, 2004, 8(1): 1—13.

[9] 李晓梅, 莫则尧. 多重网格算法综述[J]. 中国科学基金, 1996, 10(1): 4—11.

Simulated annealing based on multigrid

TAO Qing-yun

(College of Mathematics and Computer Science, Hunan University of Arts and Science, Changde 415000, China)

Multigrid methods have been proven to be an efficient approach in accelerating the convergence rate of numerical algorithms for solving partial differential equations. In order to accelerate the convergence rate of simulated annealing, a novel simulated annealing based on multigrid is proposed and its convergence is proven. The algorithm is tested on a set of 13 well-known benchmark functions. Experiment results demonstrate that multigrid methods can accelerate the convergence rate of Simulated Annealing, and improve their performance.

Simulated Annealing; Multigrid; Function optimization.

10.3969/j.issn.1672-6146.2013.04.002

O 241.8

1672−6146(2013)04−0008−04

email: 17734524@qq.com.

2013-09-28

(责任编校:刘晓霞)