Granger因果关系检验的模型选择与相关策略研究

吕光明

（北京师范大学 国民核算研究院，北京 100875）

Granger因果关系检验的模型选择与相关策略研究

吕光明

（北京师范大学 国民核算研究院，北京 100875）

运用Granger因果关系检验识别确定经济变量间因果关系是经济研究中极为常见的分析模式，然而在具体应用时，Granger因果关系检验的功效会受到模型形式选择与检验策略因素的影响，为此，解析了Granger因果关系检验的水平型VAR、差分型VAR、VEC三种模型形式选择的基本原理，探讨了与模型选择相关的四大检验策略，即变量个数选择、滞后阶数选择、变量单整性检验、协整空间维数选择，并给出了Granger因果关系检验相对稳妥的实践操作程序。

Granger因果关系检验；模型选择；检验策略

在经济分析中，很多时候需要关注变量间存在的强相关关系能否转变为因果关系。尽管有时可以从理论上对因果关系的方向做出初步判断，但由于所依据的假设前提并不完全一致，这就使理论上断定的方向出现差异，甚至完全相反。这些理论上的争议通常是经验研究关注的焦点，其因果关系方向的有效识别更是其中的核心问题。

运用Granger因果关系检验识别确定变量间因果关系是经验研究中极为常见的分析模式。据中国期刊网数据检索显示，1998年至今，国内以“格兰杰（Granger）检验”、“格兰杰因果检验”、“格兰杰因果关系检验”作为关键词的经济管理类论文达4 263篇之多。然而，研读这些论文可以发现，不少文章由于缺乏对方法适用范围和前提条件的深入了解，在Granger因果关系检验的模型选择和策略选择上存在或多或少的随意性，甚至有错误或不当之处。一些学者如庞皓和陈述云、周建和李子奈、王立平和龙志和、曹永福、陈雄兵和张宗成等曾对Granger因果关系检验中需要注意的问题做过学理上的探讨［1－5］，但这些探讨较少地与实践操作程序相结合，不利于广大学者消化吸收并在具体应用研究时准确把握。本文在国内外研究文献的基础上，深入讨论分析Granger因果检验的模型选择和检验策略问题，并给出具体检验操作程序。

一、Granger因果关系检验模型的形式选择

Granger因果性的概念，准确地说是Granger非因果性（Granger noncausality，简称 GNC）的概念，是建立在一个变量X的过去和另一个变量Y的过去对变量X的可预测性的基础上。特别地，当预测X时，如果加入Y过去值后的预测结果，比仅仅使用X过去值的结果更准确，就说Y是X的Granger原因。因此，Granger因果关系可以更多地理解为预测关系或领先关系，而不是一般意义上的因果关系。

抛开理论问题不谈，Granger因果关系检验在具体检验操作时还存在不少方法论问题。其中，对检验操作程序产生决定性影响的是数据生成过程（DGP）特征。由于Granger因果关系检验构造的是Wald类型的统计量，该统计量会随着所检验变量的平稳性和协整关系等特征的变化而呈现出不同的渐近表现形式，因此，有必要根据DGP特征选择相应的模型形式。

（一）水平型VAR模型形式的Granger因果关系检验

尽管Granger因果关系检验最初提出时并没有规定所检验变量必须是平稳过程，但事实上隐含这一假定。换句话说，当检验变量为平稳过程时，Granger因果关系检验的模型形式是水平型VAR模型。对于n×1变量样本序列xt＝（x1t，x2t，…，xnt）′，其k阶滞后的水平型VAR模型系统可表示如下：

基于WL统计量进行Granger因果关系检验的基础是渐近理论，而渐近理论仅对平稳变量有效。若VAR模型系统含有非平稳变量，则WL统计量的渐近分布变化很大。当水平型VAR模型系统不含有截距项或时间趋势项时，WL统计量会出现一个与干扰参数和有限分布无关的非标准分布；当水平型VAR模型系统仅含有截距项，且其中序列存在协整关系时，WL统计量会出现一个与干扰参数有关的非标准分布；当水平型VAR模型系统中序列非充分协整（insufficiently cointegration）时，WL统计量会出现一个依赖于干扰参数的有限的非标准分 布［6］。为 此，Toda 和 Yamamoto、Dolado 和Lütkepoh在水平型VAR模型系统框架下给出了GNC检验的渐近χ2分布［7－8］，这种分布无需考虑系统单整或协整性质。具体地，为了消除非平稳变量情形下OLS估计量协方差矩阵的奇异性，只需在式（1）中引入扩展的滞后期阶数即可：

其中，dmax为xt中变量元素的最大单整阶数。Toda和Yamamoto证明了当最大单整阶数为d时，WL同样渐近服从χ2分布［7］。显然，其检验操作原理并无太大变化。

（二）VEC模型形式的Granger因果关系检验

当xt中元素变量非平稳时，由于一些估计系数或其线性组合可能会比T更快收敛地得到有效估计，因而会导致OLS估计量的渐近分布出现奇异性，进而出现一个依赖于干扰参数的有限的非标准分布［6］，此时，一个有效的解决办法是将VAR模型转换为等价VEC模型，再进行GNC检验。令Δxt＝xt－xt－1，水平型VAR模型可以转换为如下形式的VEC模型：

其中，α为反映系统偏离非均衡时调整速度的矩阵，β为反映长期均衡关系的协整向量矩阵，其每一行均为一协整向量。尽管本身不是唯一的，但唯一地定义一个协整空间。

在VEC模型中，对于零假设H0：从xm到xs的因果关系不存在，式（4）的参数可借助于Johansen提出的最大似然方法估计得到，此时，＾π为π＝vec［Γ1，…，Γk－1，αβ′］的估计量，θij为与π相关联的选择矩阵。利用式（2）就可计算得到 Wald统计量，不妨记为WEC。当然，我们也可以通过如下转换关系获取水平型VAR模型参数的估计值，进而借助于式（2）计算WEC统计量：

在零假设H0下，WEC统计量渐近服从χ2分布，进而可以进行GNC检验了。

（三）差分型VAR模型形式的Granger因果关系检验

当检验变量为非平稳过程，且变量间不存在协整关系，即r＝0时，式（4）中的∏ ＝0，不存在所谓的ECM，因此基于VEC模型的Granger因果关系检验也就无从谈起。此时，一个可行的解决办法是：先对变量差分使其变为平稳，然后再仿照水平型VAR模型形式来进行GNC检验。这就是差分型VAR模型的Granger因果关系检验，其模型形式如下：

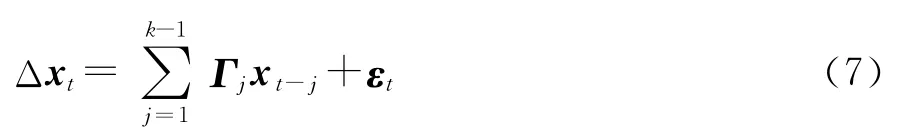
在此情形下，对于特定的GNC零假设H0，可根据式（7）的估计结果，借助于式（2）得到 Wald检验统计量，记为 WD。其中，＾π为π＝vec［Γ1，Γ2，…，Γk－1］的估计量，θij为与π相关联的选择矩阵。

在具体应用时，如果部分变量平稳，部分变量非平稳但不存在协整关系，此时可采用部分差分的VAR模型，即平稳变量进入模型的形式是水平形式，而非平稳变量的进入形式则是差分后的平稳形式。由于差分使变量的平稳性发生变化的同时也改变了变量的经济含义，因此在解读Granger因果关系检验结果时应加以注意。

需要指出的是，在Granger因果关系检验中，基于扩展滞后期阶数的水平型VAR模型的检验是一种相对独立的检验方法，如果在实践中采用这种方法，就不需要考虑三种模型形式的选择问题。与严格选择三种模型形式的检验做法相比，扩展滞后期阶数的水平型VAR模型检验由于需要纳入更多的滞后项会在检验效率上产生损失。Dolado和Lütkepohl、Giles和Mirza等研究表明，大样本情形下，上述效率损失与GNC检验结果的准确性提高相比要小得多，而小样本情形下则恰恰相反［8－9］。

二、Granger因果关系检验的相关策略

（一）Granger因果关系检验模型变量个数的选择

Granger因果关系检验中的GNC定义是建立在变量间可预测性的基础上，其中的预测性是相对信息集而言的。GNC最初定义中的信息集是包含到目前为止所有相关变量的完全信息集，但在实际检验中通常很难得到完全信息集，因而必须大大缩小信息集的范围，此时，如何选择变量定义信息集就成为一个重要的问题。由于实际问题大多集中在对两个变量间因果关系的检验，因而上述问题又转换为：除了需要检验的两个变量外，在信息集中是否需要增加一些其他相关变量？或者说，Granger因果关系检验基于双变量模型框架，还是多变量模型框架？

从计量经济理论上看，Granger检验的模型系统将所有相关变量均视为内生变量，不需要过多关于变量间关系的先验约束，因而在一定意义上是泛理论的（atheoretical），但这并不意味着可以脱离理论基础进行简化分析。Caporale和Pittis曾指出，过度简化的二元VAR或VECM模型系统可能存在“遗漏变量偏误（omitted variable bias）”，即丢失了第三方影响因素信息而导致计量模型的“不完整”性，进而得出“虚假”的 Granger因果性结论［10］。Granger、Asghar等进一步指出，信息集中遗漏重要变量很可能导致“虚假”的因果性结论，此时如果能够恰当地拓展信息集合，把重要的变量引入信息集，原来的“虚假”因果性可能消失［11－12］。

尽管多变量模型有可能得到比双变量模型更为准确的因果关系结论，但它也存在两个缺点：一是自由度问题。现实检验中时间序列的样本容量是有限的，此时，增加变量会使模型自由度迅速减少，出现过度拒绝或拒绝不足的水平扭曲（size distortion）问题，进而导致检验结果失真。二是无关变量的干扰问题。由于因果关系检验结果对模型结构比较敏感，过多无关变量进入检验模型会影响检验结论，因此，Granger检验模型到底是选择多变量还是双变量，主要取决于理论分析判断。正如Asghar所指出的，理想的所有混合因素变量可控的Granger因果关系检验仅存在于实验研究中，而非现实研究中［12］。经济理论必须为发现真实的因果关系提供必要支持，研究者必须深入研究实际问题而非进行统计分析①洪永泰（2007）也曾在《经济研究》撰文指出，统计方法与工具，不管是数理统计还是经济统计，均不能确认经济变量之间关系是否为因果关系。因果关系的确认，必须借助于经济理论的指导。。

（二）Granger因果关系检验模型滞后阶数的选择

由于VAR模型和VEC模型对xt的滞后阶数有很强的敏感性，因此具体Granger检验时，需要对不同的滞后阶数进行试验，以确信因果关系结论是强健的，不依赖于检验模型。一般做法是：从给定的滞后阶数上界kmax出发，采用一些检验准则进行阶数选择。其中，kmax的取值依赖于数据样本容量T。对于年度数据，kmax通常取3；对于季度数据，kmax通常取8；对于月度数据，kmax通常取18［13］98－12，另外也可取kmax＝int［12（T／100）1／4］或int［（T）1／3］。滞后阶数的检验准则多是通过向前一步预测误差的均方差∑

x（1）构造的，常见的检验准则有赤池信息准则（AIC）、施瓦茨准则（SC）和汉南—奎因准则（HQC）等三种，根据样本容量T、参数个数m和滞后长度，三种准则对∑x（1）施以不同惩罚如下：

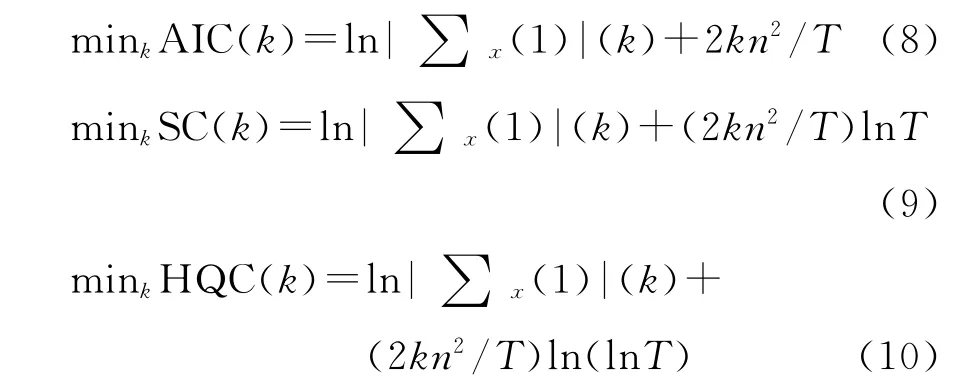
在进行Granger因果关系检验时，T通常较大，n大于1，因此，AIC准则具有选择过大滞后阶数的倾向，而HQC准则和SC准则在选择正确滞后阶数时具有较强的一致性。Ivanov和Kilian通过比较研究发现，HQ准则最适用于季度和月度数据研究［14］。不过，Cheung和Lai也指出，在过低阶数的模型设定可能导致协整空间维数r出现错误推断的情况下，AIC选择的过大滞后阶数做法则更为可取［15］。

（三）Granger因果关系检验模型变量的单整性检验

从第一部分的研究看，Granger因果关系的三种模型形式均需要进行单位根检验，确定变量的单整阶数。理论上，可以进行单位根检验的方法很多，主要有DF和ADF检验法、PP检验法、霍尔工具变量法、DF-GLS检验法、KPSS检验法等五种。这些检验方法的共同点是，基于过程理论和在此基础上建立起来的泛函中心极限定理构造的检验统计量进行检验；不同点表现在，在不同的零假设和备择假设下对扰动项可能的相关特性的处理方法不同。对于零假设的选择，前四种检验方法选择差分平稳模型，KPSS检验法则选择趋势平稳模型。对于DF检验中扰动项可能的相关特性的处理，ADF检验法使用增加滞后差分项的估计方法，霍尔工具变量法使用工具变量估计方法，DF-GLS检验法使用广义最小二乘法估计方法，KPSS检验法采用不改变估计方法的非参数修正方法，这些不同的选择和处理直接导致五种检验方法在模型形式、统计量的构造、使用要求等方面存在着较大的不同。

单位根检验是一个相当复杂的问题，其模型形式、统计量的构造、滞后阶数的选取都会影响单位根检验的功效，进而通过后续建立的模型 “潜在地”影响Granger因果关系检验的结果。在有限样本情形下，使用前述五种单位根检验方法可能会得出不同结果，因此实际检验时，有必要根据数据特征选取合适的方法。若数据特征未知，最好使用多种方法进行检验，并对不同形式的检验结果进行比较和统一，以求得到相对可靠、合理的结论［16］。特别地，在采用水平增广型VAR模型进行因果关系检验时，如果样本容量允许，还可以采取最为保守的最大单整阶数，以保证结果的稳健性。

（四）Granger因果关系检验模型协整空间维数的选择

在采用VEC模型进行Granger因果关系检验之前，需要解决的一个关键问题是，如何进行协整检验，并准确确定协整空间的维数r。Clark和Mirza通过模拟实验指出，如果错误估计协整空间的维数，则可能导致GNC零假设的过度拒绝［6］。

关于协整关系的检验方法有多种，其中较为常用的是Engle-Granger两步法和Johansen检验法。Engle-Granger两步法采用两阶段回归来检验，首先对同阶协整变量进行最小二乘回归，然后对回归残差进行ADF单位根检验。拒绝存在单位根的零假设是协整关系存在的证据。Engle-Granger两步法的缺点是：小样本情形下通过两步OLS估计得到误差通常较大；不能应用于三个以上的多变量情形，且在应用于双变量时，变量回归互换位置后有可能得到不一致的协整检验结果。Johansen检验法是一种用极大似然估计来检验多变量之间协整关系的方法。假设矩阵的秩为r，其按大小排列的非零特征根分别为λ1，λ2，…，λr。具体地，Johansen检验通过下面两个检验统计量来考察矩阵∏的特征根的显著性并求得协整空间的维数r：

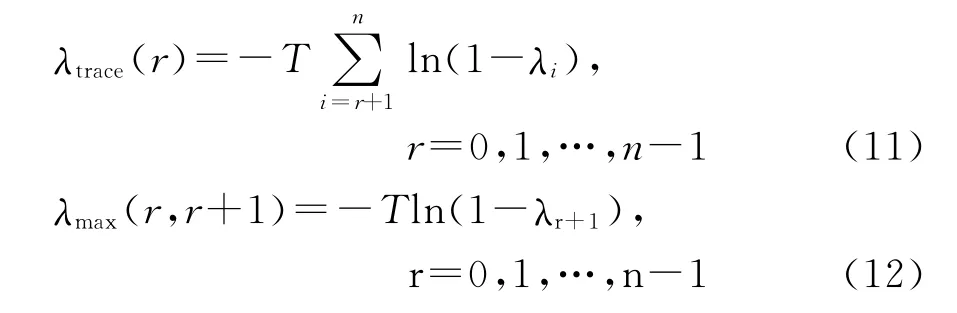
其中，式（11）为迹检验统计量，式（12）为最大特征根检验统计量。

在实际检验中，有两点问题需要注意：一是迹检验和最大特征根检验两个统计量的结果有可能发生冲突，此时可以根据协整结果的解释能力选择相应的结论。二是协整检验结果对确定性趋势的选择非常敏感，研究者需要在没有确定性趋势项、有线性趋势和二次趋势等三种情况下对五种模型形式进行选择。通常基于不同的检验方程往往可得到不同的Granger因果关系检验结论。以迹检验统计量为例，具体选择可根据Pantula原则，从约束最多的模型出发直到约束最小的模型，借助于如下渐近统计量进行检验：

三、Granger因果关系检验的实践操作程序

理论上，Granger因果关系检验可采用水平型VAR、差分型VAR、VEC三种模型形式，且在每一种模型形式中变量个数、滞后阶数、变量单整阶数、协整空间维数等又可能有所不同，因此，对于同一组待检验变量样本，不同研究如果不认真考虑经济理论和斟酌检验细节，随意设定模型形式，就有可能得到不同的检验结果。那么，到底应该遵循那一个结果进行经济意义分析呢？结合上述前两部分内容及Clarke和 Mirza、Lütkepohl等研究结论［6］［17］5－7，这里对Granger因果关系检验的实践操作步骤归纳总结如下：

第一步，根据理论和过去经验研究，选择确定待检验变量及其序列形式。这一步主要解决两大问题：一是检验所包含模型的变量个数n；二是每个变量的数据序列是采用定基形式还是环比形式？数据处理是否需要进行季节调整，是否需要取对数？等等。

第二步，借助于单位根检验、协整检验等手段甄别变量序列的时序特征，进而选定合适的Granger因果检验模型形式。具体地，首先应对所有变量进行单位根检验，确保所有变量具有相同的单整阶数d，然后按照如下原则来选择相应的检验模型形式：（1）在所有变量的单整阶数d或已知且样本容量足够大的情况下，应选择常规的或扩展滞后期阶数的水平型VAR模型进行因果关系检验；（2）在单整阶数d大于零的情况下，因果关系检验模型的形式选择依赖于变量间协整关系检验结果。此时，如果协整关系存在，则应选择VEC模型进行因果关系检验；如果协整关系不存在，则应选择差分型VAR模型进行检验。

第三步，依据前一步选定的Granger因果检验模型，在样本容量容许的情况下，采用AIC准则、SC准则和HQC准则中一种或多种来确定检验模型的最优滞后阶数k。

第四步，估计Granger因果检验模型，并进行相应的模型设定检验和模型稳健性检验。模型设定检验和模型稳健性检验的根本目的是保证模型的各种假定得到数据的支持，即模型统计适切性［18］。如果模型设定检验和模型稳健性检验暴露出问题，就应当回到第一步，重新选择模型变量，重新考虑模型形式设定，重新进行相应检验，直至通过检验为止。Clarke和Mirza等通过模拟研究发现，在平稳、单整、协整等不同的数据生成过程特征下，与常规的水平型VAR模型、差分型VAR模型、VEC模型相比，扩展滞后期阶数的水平型VAR模型的检验结果具有更好的稳健性。

第五步，基于不同模型形式对应的检验统计量对GNC的检验，分析得出相应的研究结论。Granger因果关系检验的经济意义是研究的最终目的，适当合理地分析得出模型的经济意义是研究中务必要注意的问题。

根据上述操作步骤，Granger因果关系检验实践操作程序可用流程图表示如下：

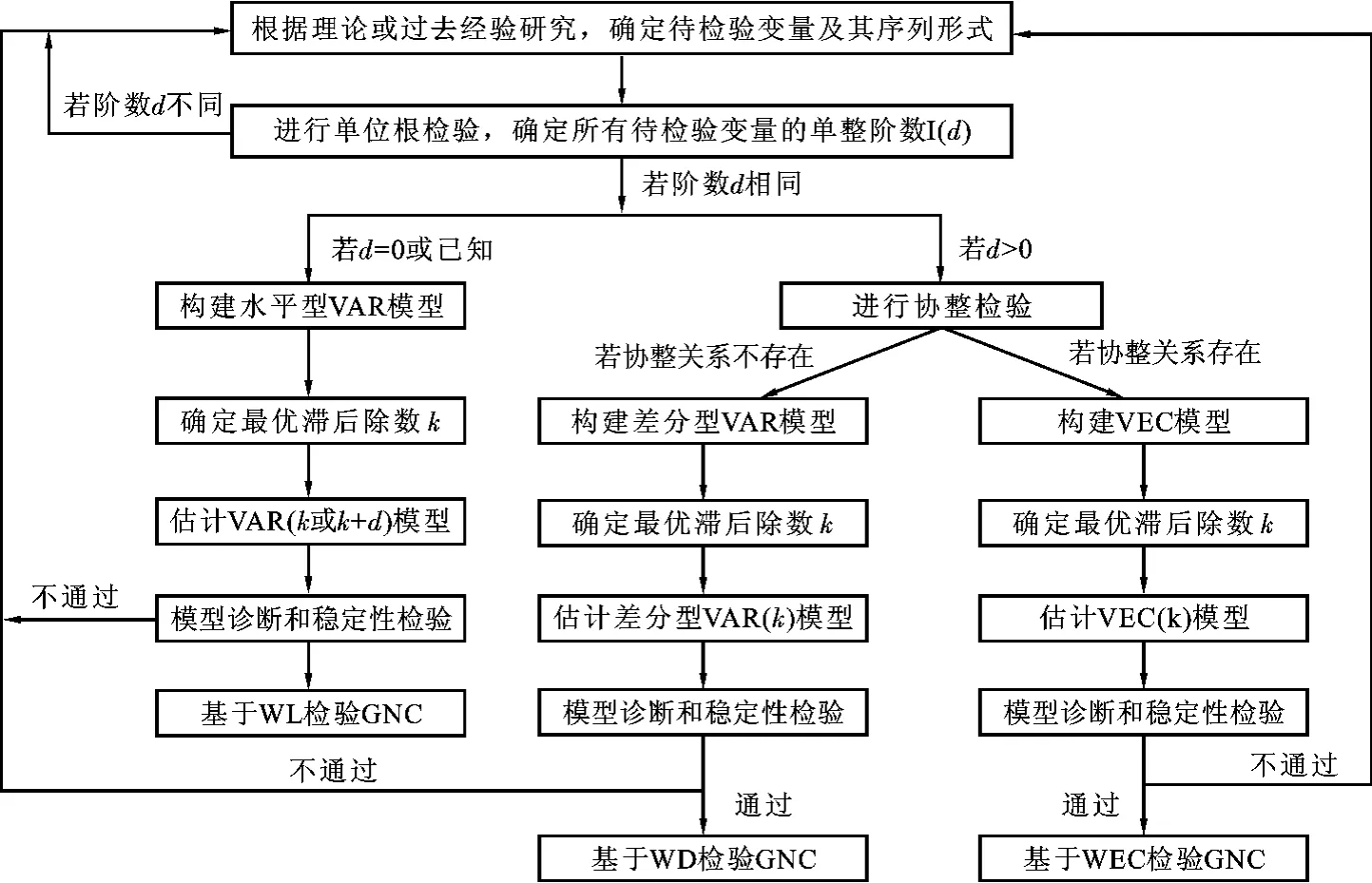
图1 Granger因果关系检验实践操作程序流程图

最后需要指出的是，作为一种基于VAR系统构造Wald检验来检验因果性的方法，其检验功效会受到模型形式与滞后阶数、变量个数与单整性、变量间协整特征等因素的影响。尽管在实践中采取相对科学的检验操作程序可以提高检验功效，但是，现实时间序列数据尤其是宏观经济数据的样本容量通常是有限的，这必然导致检验结果具有一定的随机性，换句话说，Granger因果关系检验的结果永远也不可能达到百分之百的准确。要通过Granger因果关系检验来准确识别变量间的因果关系，还有很多课题需要未来进一步研究。

［1］ 庞皓，陈述云．格兰杰因果检验的有效性及其应用［J］．统计研究，1999（11）．

［2］ 周建，李子奈．Granger因果关系检验的适用性［J］．清华大学学报：自然科学版，2004（3）．

［3］ 王立平，龙志和．基于Granger原因的因果关系检验方法评析［J］．合肥工业大学学报，2005（4）．

［4］ 曹永福．格兰杰因果性检验评述［J］．数量经济技术经济研究，2006（1）．

［5］ 陈雄兵，张宗成．再议 Granger因果检验［J］．数量经济技术经济研究，2008（1）．

［6］ Clarke J A，Mirza S A．Comparison of Some Common Methods of Detecting Granger Noncausality［J］．Journal of Statistical Computation and Simulation，2006，76（3）．

［7］ Toda H Y，Yamamoto T．Statistical Inference in Vector Autoregressions with Possibly Integrated Processes［J］．Journal of Econometrics，1995，66（1－2）．

［8］ Dolado J J，Lütkepoh H．Making Wald Tests Work for Cointegrated VAR Systems［J］．Econometric Reviews，1996，15（4）．

［9］ Giles J A，Mirza S．Some Pretesting Issues on Testing for Granger Noncausality［C］．Econometrics Working Papers 9914，Department of Economics，University of Victoria，1999．

［10］Caporale G M，Pittis N．Causality and Forecasting in Incomplete Systems［J］．Journal of Forecasting ，1997，16（6）．

［11］Granger C W J．Testing for Causality：Personal Viewpoint［J］．Journal of Economic Dynamics and Control，1980，2（1）．

［12］Asghar Z．Simulation Evidence on Granger Causality in Presence of a Confounding Variable［J］．International Journal of Applied Econometrics and Quantitative Studies，2008，5（2）．

［13］Canova．应用宏观经济研究方法［M］．周建，译．上海：上海财经大学出版社，2009．

［14］Ivanov V，Kilian L．A Practitioner＇s Guide to Lag Order Selection for VAR Impulse Response Analysis［J］．Studies in Nonlinear Dynamics and Econometrics，2005，9（1）．

［15］Cheung Y W，Lai K S．Finite－sample Sizes of Johansen＇s Likelihood Ratio Tests for Dickey Cointegration［J］．Oxford Bulletin of Economics and Statistics，1993，55（3）．

［16］吕光明．对数据平稳性检验方法的比较研究［J］．财经问题研究，2004（6）．

［17］Lütkepoh H．New Introduction to Multiple Time Series Analysis［M］．Berlin：Springer Publishing Company，2007．

［18］王美今，林建浩．计量经济学应用研究的可信性革命［J］．经济研究，2012（2）．

A Research on Model Selection and Related Strategies of Granger Causality Test

LV Guang-ming
（Institute of National Accounts，Beijing Normal University，Beijing 100875，China）

It's a very common mode of analysis in empirical research of economics to use Granger causality test to identify causality relationship between variables．However，factors like model selection and detection strategy usually have an effect on the power of Granger causality test．Therefore，it is very important to search robust operating procedures for Granger causality test and to find scientific result for causality relationship．This paper firstly analyzes basic principles of three models of Granger causality test，i．e．，maximize reduce horizontal VAR model，differential VAR model and VEC model．Then explores four test strategies related to model selection，including selection of number and lag order of variables，test of stationarity and selection of dimensions of cointegration space．Finally it puts forward a relatively robust operating procedures for Granger causality test．

Granger causality test；model selection；test strategy

F224．0

A

1007－3116（2013）03－0003－07

2012－11－10；修复日期：2012－12－19

国家社会科学基金重大招标项目《国家统计数据质量管理研究》（09＆ZD040）；教育部人文社会科学规划项目《CPI偏差理论、测度方法与中国应用研究》（12YJC910005）

吕光明，男，河南洛阳人，经济学博士，副教授，研究方向：宏观经济统计分析与计量分析。

（责任编辑：杜一哲）