纤维滤料在容尘阶段的过滤性能实验研究

林忠平，吴昌甫，龙大海，吴 淼

（1.同济大学 机械与能源工程学院，上海 201804；

2.浙江朝晖过滤技术股份有限公司，浙江 桐乡 314511；3.浙江金海环境技术股份有限公司，浙江 诸暨 311817）

随着工业的迅猛发展，空气污染问题越来越严重；同时，现代科学和现代工业，特别是电子、精密机械、冶金、宇航、核能、化工等工业以及医疗、制药、食品等行业的发展，对工艺环境的空气洁净度也提出了更高的要求［1］.目前，解决空气质量问题最有效的方法就是空气过滤.对于纤维过滤介质，孔隙率／填充率和纤维直径及其厚度决定了其过滤性能的基础结构参数.在粉尘或气溶胶微粒沉积阶段，过滤介质的孔隙率／填充率和纤维之间的孔隙尺寸均会随着粉尘积聚量的增加而发生变化，特别是在粉尘初层以及“树枝状”粉尘层形成之后，基于稳态过滤的传统理论不再适用于大部分生命周期内的积尘过滤问题.

在非稳态过滤过程中，很多学者试图从理论上描述容尘纤维滤料的压降和捕集效率数学模型（如Kozeny-Carman方程、Rudnick-Happel方程［2］）.Al-Otoom［3］借助于颗粒物过滤的数理统计模型来预测粉尘层的厚度和孔隙率、过滤效率和压降等结构、性能参数和平均微粒直径与过滤介质的平均孔隙尺寸之比的关系，并通过非线性回归得到压降的表达式.Chikao Kanaoka和Sotoji Hiragi［4］基于粉尘在圆柱纤维体上的沉积模型，提出容尘阶段等效纤维直径dfm的概念，在一定的过滤条件下得到瞬时压降Δpm（t）与dfm和阻力系数Fm的积分式.

D.Thomas和P.Penicot等［5］采用荧光素纳气溶胶对纤维过滤器在阻塞情况下捕集效率随捕集粉尘质量的变化关系进行研究.采用粘性胶带片将含尘滤料切片分成几个薄层，利用扫描电镜观察粉尘颗粒在过滤器表面和深层沉积的结构，基于Bergman模型和Payet模型［6］，提出适合深层过滤和粉尘层之间的过渡区域的效率经验公式.

由于Chikao Kanaoka和Sotoji Hiragi模型中的容尘阶段瞬时压降的表达式求解较为复杂，需要结合具体的过滤模型，并且Chikao和Sotoji也没有给出确切的解，而是从实验分析的角度探讨几个参数对压降Δpm的影响.D.Thomas模型在引入Payet模型时忽略了惯性碰撞的影响，并且进行扫描电镜观察的切片滤料厚度大多数在10－4～10－3m数量级，很难实现，操作误差很大，很容易破坏原有粉尘层结构及其内部填充密度.因此，目前非稳态压力损失和过滤效率的研究，尚不能全面反映过滤过程中的真实情况.本文基于空气滤清器性能试验装置，选用几种具有代表性的合成纤维过滤介质进行容尘实验，采用Welas-2000气溶胶粒径谱仪测试纤维滤料在不同容尘阶段的分级效率.同时利用HITACHI S-2360N 和 HITACHI S-3400N 扫描电子显微镜观测分析清洁滤料及不同容尘阶段的滤料的结构与相关参数的变化，对影响纤维过滤介质的非稳态过滤性能参数（如容尘阶段各粒径微区间的分级效率和压降Δp等）的重要参数（如气溶胶及粉尘特性参数、积尘填充率α、孔隙率ε等）进行研究探讨，并利用实验数据检验比较具有代表性的关于非稳态过滤的压降经验公式的适用性，借助于Matlab的回归分析拟合出合适的压降修正式.

1 纤维滤料的物性参数

过滤是分离技术的一种，主要是依托过滤材料将悬浮在流体中的固体颗粒物分离出来［7］.过滤方式有滤芯、滤网、滤布、滤纸、滤袋和膜；过滤介质主要有纤维滤料、复合滤料和功能性滤料等.由于纤维滤料具有比表面积大、体积蓬松、价格低廉、容易加工、多孔性和柔性等优点［1］，现已成为空气过滤材料的主导产品，使用原料有天然纤维（如棉、毛、麻等）和非天然纤维两种.其中，非天然纤维包括无机纤维（如玻璃纤维和金属纤维）和有机纤维（如人造纤维和合成纤维），人造纤维主要有纤维素和蛋白质［8］，合成纤维则包括聚酯（PET）、聚丙烯（PP）、聚酰胺、聚苯硫醚（PPS）、聚四氟乙烯（PTFE）、芳族聚酰亚胺、偏芳族聚酰胺、三聚氰胺等［9］.

合成纤维具有过滤效率高、成本低、易与其他滤料复合等优点，且容易进行打褶、折叠、模压等深加工，因此广泛应用于过滤与分离行业中［10］.合成纤维的各种加工技术，如湿法、化学粘合法、针刺法、纺粘法、热粘合及熔喷法等都适用于过滤材料的生产［11］.表1列出了几种不同工艺加工的过滤材料的性能参数.

表1 几种不同工艺加工的过滤材料的性能参数［12］Tab.1 Performance parameters of the filtering materials by several different processing technologies［12］

由于纤维直径及其孔隙间尺寸均为微米级，需采用扫描电子显微镜进行观测.本文采用的HITACHI S-2360N 和 S-3400N（其分辨率均为3 nm，放大倍数分别为20～20万、5～30万）具有二次电子探测、背散射电子探测以及低真空模式，可进行点、线、面定性和定量分析，定量分析精度在0.5%以内.通过对纤维滤料的扫描电镜观察，可以得到受试滤料的纤维直径、孔隙间尺寸、填充率α、孔隙率ε，采用游标卡尺和电子天平测量受试纤维滤料的厚度和质量，结果如表2所示.试样B的电镜扫描图见图1.

2 非稳态过滤性能实验

2.1 气溶胶特性对非稳态过滤性能参数的影响

由于过滤介质在容尘阶段的分级效率和压降Δp等非稳态过滤性能参数与微粒浓度、Sauter平均直径D32以及粒径分布等气溶胶特性参数密切相关，且根据文献［13］对气溶胶特性的实验研究和分析计算结果可知，气液质量比、喷雾溶液的物理性质（如表面张力和动力粘度）以及气液相对速度和气体密度的变化均对发生气溶胶的特性参数起着决定性的作用，故有必要结合本节实验深入探讨分析气溶胶的特性参数对纤维滤料的过滤性能参数的影响.

表2 纤维滤料在清洁状态时的物性参数Tab.2 Properties of fibrous media in the clean state

图1 试样B在51.5Pa压降时的电镜扫描图（×300）Fig.1 SEM picture for the fibrous sample B at the pressure drop of 51.5Pa（magnified by 300）

选用表2中的滤料试样B，通过调节气体流量产生不同强度的气动力作用引射液体流量，并产生一组不同的气液相对速度和气液质量比（如图2和表3所示），随之利用 Welas-2000气溶胶粒径谱仪分别测量试样B上、下游的粒子数量浓度、质量浓度和Sauter平均直径D32，并分析计算在不同的气液质量比条件下分级效率随粒径的分布，如图3所示.以不同质量分数的KCl溶液作为喷雾工质以观察气溶胶发生溶液的物理性质（如表面张力和动力粘度）对纤维滤料的非稳态过滤性能的影响，如图4所示.当对比参数为气液质量比时，实验条件为5.0%（质量分数）KCl喷雾溶液、压缩空气的输出压力Δpout＝0.3MPa；当对比参数为不同质量分数的KCl雾化气溶胶时，实验条件为压缩空气的输出压力Δpout＝0.3MPa（从而气相密度保持不变），压缩空气的流量Qg＝2.52m3·h－1，气液质量比为＝22.958.

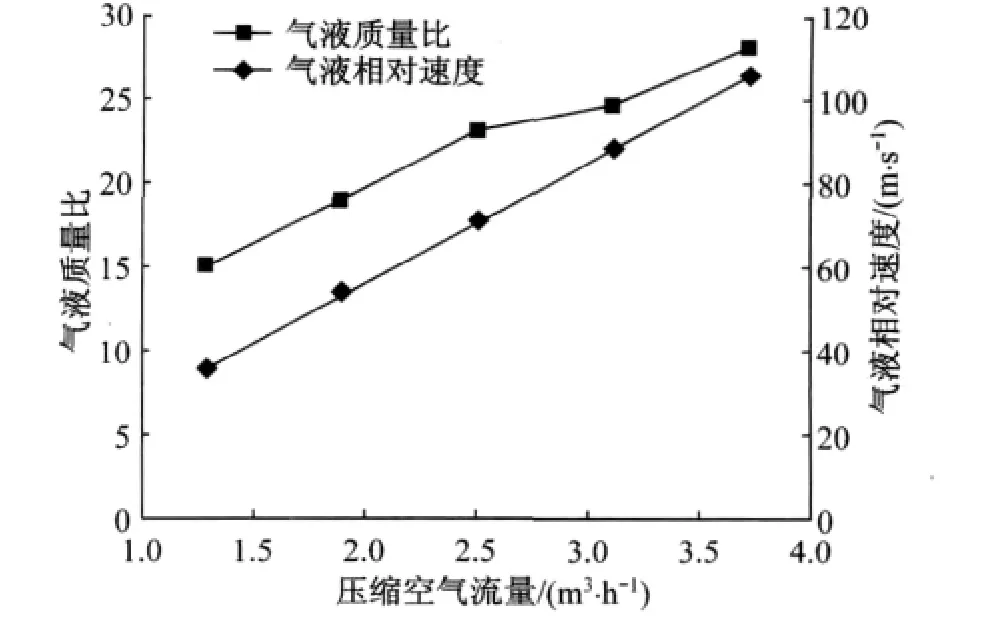
图2 滤料试样B的气液相对速度和气液质量比与压缩空气流量的关系Fig.2 The relationship between gas-liquid relative velocity and the compressed air flow rate of fibrous sample B

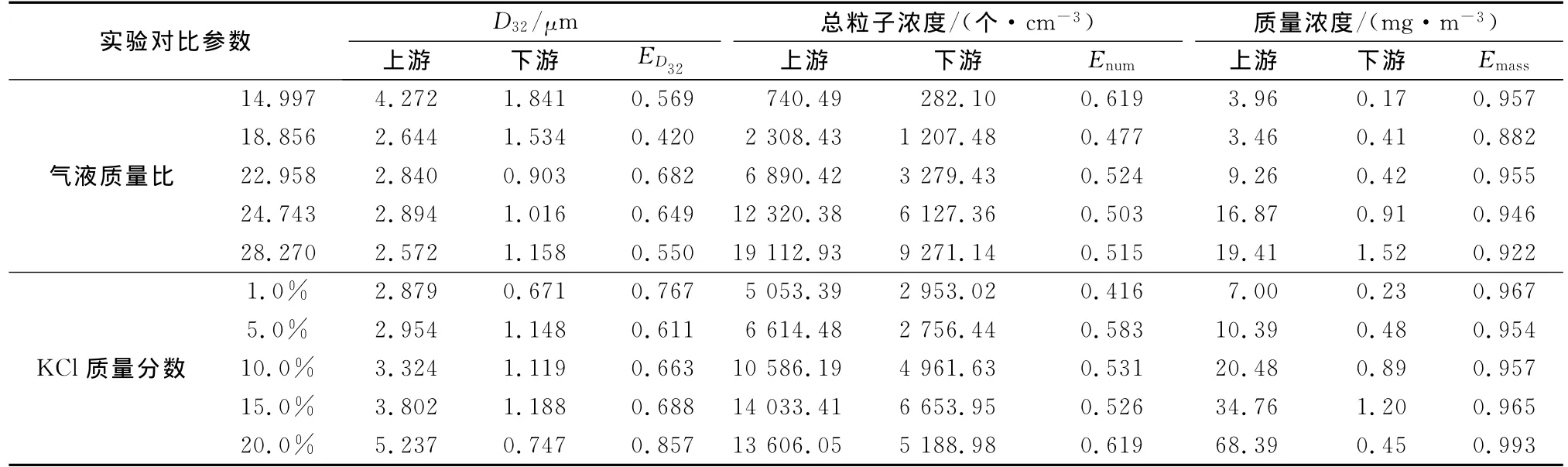
表3 滤料试样B分别在不同气液质量比和不同质量分数KCl雾化气溶胶条件下的过滤效率Tab.3 Several filtration efficiency of fibrous sample B for aerosol atomization by different gas-liquid and mass fraction of KCl solution

由表3可以看出，以Sauter平均直径D32为基准的过滤效率ED32可以反映不同气液质量比以及不同物理性质的溶液进行喷雾等条件下的过滤效率之间的差异，故可用ED32近似表示过滤介质的综合过滤性能.由图3可知，当气液质量比较小（14.997～18.856）时，过滤效率随粒径的分布较为发散，出现严重的振荡；而当气液质量比逐渐增大（22.958～28.270）时，过滤效率随粒径的分布趋于集中，并且各粒径微区间的效率值有较小幅度的增加.由图4可以发现，当雾化溶液KCl的质量分数较小（1.0%～5.0%）时，过滤效率随粒径的分布出现一定的振荡；而当 KCl溶液的质量分数增大（10.0%～20.0%）时，过滤效率随粒径的分布趋于集中，并且各粒径微区间的效率值有一定程度的增加.

2.2 纤维滤料在容尘阶段的过滤性能实验

使用ISO12103-1A2试验粉尘通过人工尘发生器以一定的压力和气流量吹入测试主管段中，并与主管段中的风量混合均匀，以模拟纤维滤料在实际使用过程中各个不同的容尘阶段.终阻力值取为初始压降Δp0的2.5倍，将Δp0～2.5Δp0之间均分为4个阻力阶段或阻力点.在各个阻力阶段或阻力点，结合KCl多分散相气溶胶的发生由Welas-2 000气溶胶粒径谱仪进行采样分析得到不同粒径微区间（0.178～10.000μm 共56个粒径通道）的计数效率，分别如图5，6所示（以滤料试样B和C为例进行实验，其中E（pi）为第i阻力阶段（Δpi）的过滤效率值，i＝0～3）.对于表2中的纤维滤料，其压降Δp与初始压降Δp0之间的压差（Δp－Δp0）与单位面积累计容尘量的关系曲线如图7所示.

图5，6中，采用质量分数为50%的KCl溶液为喷雾工质，气液质量比为22.958，滤速为0.40m·s－1，试验风量为125.2m3·h－1.可以看出，随着粉尘颗粒在纤维滤料表面的沉积，粉尘初层以及最终“树枝状”粉尘层的形成均有助于提高各粒径微区间的分级效率，同时也显著地增加了各容尘阶段的压降值.纤维直径越小的过滤介质（如滤料试样C），在容尘阶段对各粒径微区间的分级效率越高，随发尘量的增加而增加的速率越快，且增加至100%分级效率所对应的粒径微区间也越小，但其受到的阻力越大，随之带来的运行能耗也越大，而且其容尘量也越小.经分析计算得，用于本节容尘实验的几种纤维滤料在粉尘颗粒沉积的各个压降阶段的最易透过粒径位于［0.184μm，0.407μm］区间内.

3 分析与讨论

结合H.Friess和G.Yadigaroglu的悬浮微粒模型［14］以及文献［13］中对填充率α的分析，可将纤维滤料在微粒阻塞阶段的填充率看作纤维滤料在清洁状态时的填充率与粉尘颗粒或气溶胶微粒的“沉积填充率”（沉积微粒体积Vp与总体积VT之比，假设形成粉尘层的厚度忽略不计）之和，于是经微粒沉积之后的填充率α可写作

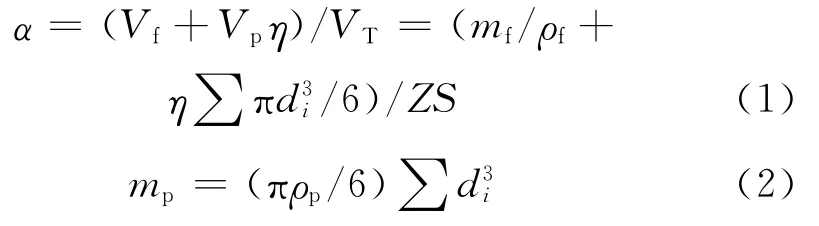
将式（2）代入式（1），可得

式（1）～（3）中：Vf为过滤介质的体积，m3；η为单纤维捕集效率；mf为过滤介质的质量，kg；ρf为过滤介质的密度，kg·m－3；di为第i个微粒直径，μm；Z为多孔过滤介质的厚度，m；S为多孔过滤介质的面积，m2；mp为过滤介质在某一阻力阶段的累计容尘量，kg；ρp为粉尘颗粒或气溶胶微粒的密度，kg·m－3，取为2.65×103kg·m－3（参照ISO12103-1A2试验粉尘说明书）.

纤维多孔过滤介质的有效孔隙尺寸，即孔径d0可通过下式进行计算［15］，其在清洁状态时的计算值与表2中的实测结果比较接近.

式中：df为纤维直径，μm.

由式（4）可推导出α的表达式为

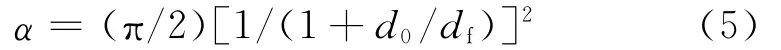
于是可通过扫描电镜图分析计算容尘阶段的纤维间孔径d0，从而间接计算出纤维滤料在容尘过程中的填充率α.由于纤维滤料在容尘之后的过滤效率较高，故可将式（3）中的单纤维捕集效率η取为1.根据纤维滤料在容尘阶段的过滤性能实验，以及填充率α的计算式，可由实验数据分析计算得积尘后的α，并整理出α与累计容尘量的关系曲线，分别如表4和图8所示.

表4 容尘阶段填充率α的计算表（根据式（3））Tab.4 Packing densityαof fibrous media on dust particle-loading stages（by Equation（3））

从图8可以看出，纤维滤料在容尘阶段的填充率与累计容尘量呈线性关系，其中拟合的趋势线的斜率和截距分别为式（3）中的常数项η／ZSρp，mf／ZSρf.滤料试样A的积尘填充率α因其容尘量较大而在［14.419%，22.634%］较宽的范围内变动，而试样C的积尘填充率α的变化范围较窄.可以发现，表4中的3种纤维滤料的积尘填充率α处于［14.419%，22.634%］，而按照文献［16］对过滤介质填充率的分类，清洁状态时的滤料试样A，B和C均属于低填充率（α＜20%）的深层过滤材料.

在本文实验中，受扫描电镜使用限制，观察前需要将容尘过滤介质表面的粉尘颗粒或气溶胶微粒及其形成的粉尘初层或“树枝状”粉尘层吹扫干净，由此破坏了纤维表面的粉尘层结构，只能观察填充于纤维深层结构中的微粒形态和纤维间孔隙率／填充率的变化情况，给准确观察粉尘层的物理结构并分析计算其结构参数的变化对过滤效率和阻力的影响造成了极大的不便.

图8 纤维滤料在容尘阶段的填充率与累计容尘量的关系Fig.8 The curves of packing densityαof fibrous media with dust loading against the cumulative dust holding capacity

由于粉尘层的微观结构极其复杂，Bergman［17］在Davies模型［18］基础上将容尘滤料前后的压降分为清洁滤料压降和树枝状的沉积物／粉尘层（看作新的过滤滤料）压降两部分.其中，粉尘层压降可套用清洁滤料的压降计算式（类似于相似准则）并作一定的均方根处理，如下式所示：

式中：Δp为纤维滤料的压降，Pa；Δpf为清洁状态时纤维滤料的压降，Pa；Δpc为粉尘层压降，Pa；K1为纤维滤料的阻力常数，取决于过滤介质的物性参数，kg·m－2·s－1；U0为滤速，m·s－1；FD为Stokes阻力；S为过滤面积，m2；μ为气体动力粘滞系数，Pa·s；Ni为粉尘层中的颗粒数；dpi为第i个粉尘粒径，μm；Ci为Cunningham滑动修正系数.

若粉尘颗粒是单分散的，且与相邻粒子不发生作用，则有［2，19］

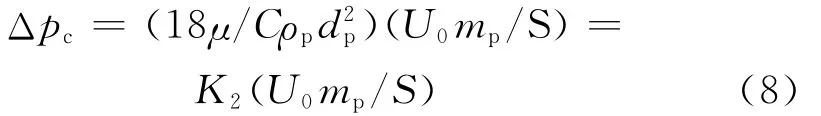
式中：ρp为粉尘密度，kg·m－3；mp为积聚粉尘质量，kg；K2为粉尘层阻力系数，s－1.

Kozeny和Carman［2］将粉尘层看作一系列平行的毛细管，其总体积和表面积等于粉尘层的中空体积以及组成粉尘层的颗粒物表面积之和，从而推导出K2的计算式为

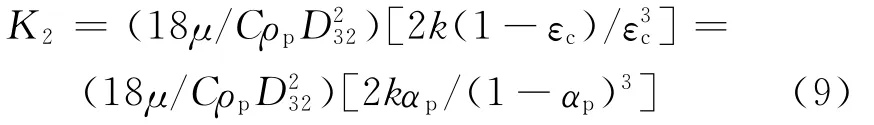
式中：D32为粉尘颗粒的souter平均直径，μm；k为Kozeny常数，对于圆形粉尘颗粒，k＝4.8，对于不规则粉尘颗粒，k＝5.0；εc为粉尘层孔隙率；αp为收集粉尘的填充率.

Bergman［17］则推导出Δp的计算式为

式中：ZL为纤维滤料加上粉尘层的总厚度，m；αf为纤维填充率.

将表2和表4中的数据代入式（8）～（10），可计算得到如表5所示的Δp值及其与实测值之间的误差.由表5可知，根据式（8）～（10）计算的Δp值与实测值相差较大，将式（9）代入式（8）之后的计算式中含有αp和mp两个容尘参数，并且关于αp的表达式较为复杂，若将式（3）代入其中则会更为复杂，若将式（5）代入其中，仍然很难从回归分析角度拟合出合适的修正式（因有效孔隙尺寸／孔径d0与mp同样存在较为复杂的关系式）.故针对式（10）进行一定的对数变换，并借助于Matlab的回归分析拟合出合适的修正式.

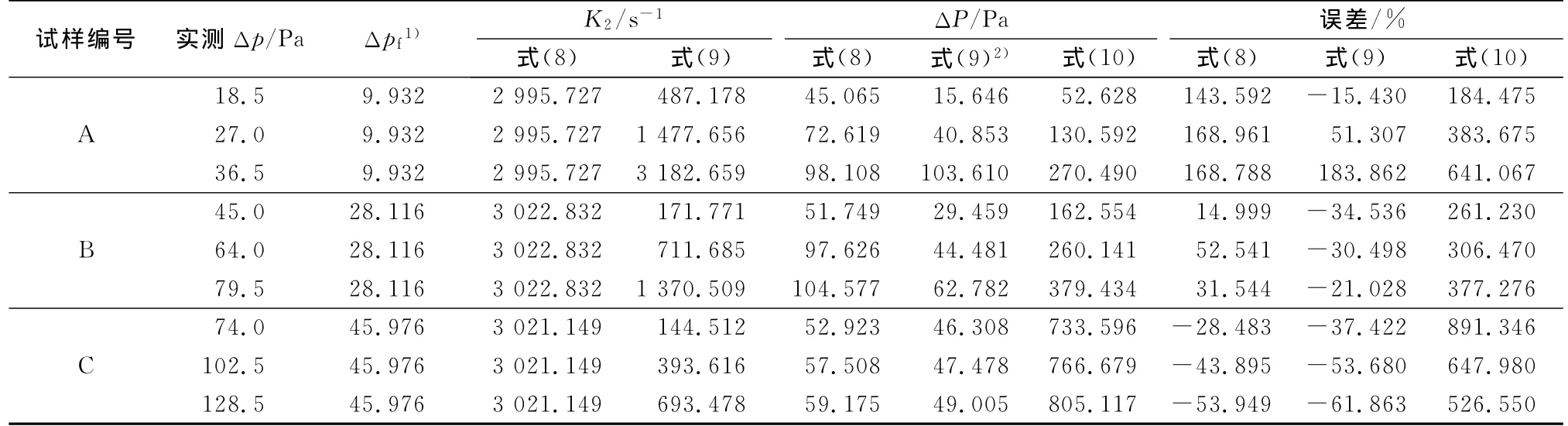
表5 据式（8）～（10）计算的Δp误差Tab.5 The error analysis for the pressure dropΔpcalculated by Equation（8）～（10）

对式（10）两边取常用对数，则有

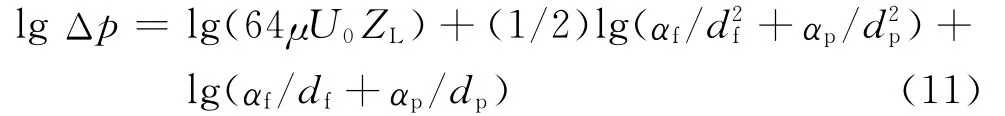
根据式（11）的形式作出如下假设：

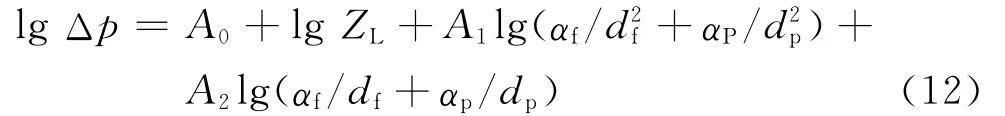
根据本文容尘阶段的实验数据，利用Matlab回归拟合出A0＝－0.093 3，A1＝0.276 2，A2＝0.803 1.然后将A0，A1和A2代入式（12），并整理得到式（10）的修正式式（11）～（13）中的Δp值均为纤维滤料在容尘阶段的压降（已扣除安装板的压降），不包括纤维滤料在清洁状态时的压降.根据式（13）计算得到的Δp值与实测值之间的误差基本保持在15%以内（除了滤料试样A和C的第3个容尘阶段的偏差分别为32.8%和30.4%之外），如图9所示.利用Matlab拟合的三维立体平面图如图10所示，其中x1，x2，x3，y分别代表Δp.

文献［13］结合实验数据探讨了一些经典的量纲为一的参数之间的内在联系及其对纤维滤料在容尘阶段的非稳态过滤效率的影响，并利用非线性回归方法分析拟合出以下纤维过滤介质的非稳态过滤效率经验公式：

式中：E（pi）为第i阻力阶段（Δpi）的过滤效率值，i＝0～3；mp为过滤介质在某一阻力阶段的累计容尘量，kg；b，c为与粉尘或气溶胶微粒的Re、拦截参数R和St等［20－22］有关的常数.

4 结论

本文通过容尘实验分析了非稳态过滤条件下压降和过滤效率随气溶胶及粉尘特性以及积尘填充率变化的规律，并借助于Matlab的回归分析拟合出合适的容尘阶段的压降修正式.通过分析与研究，得到以下结论：

（1）结合实验数据分析了气溶胶的特性参数对纤维滤料的过滤性能参数的影响.当气液质量比逐渐增大时，过滤效率随粒径的分布趋于集中，且各粒径微区间的过滤效率有较小幅度的增加.当KCl溶液的质量分数逐渐增大（喷雾工质的表面张力增大）时，过滤效率随粒径的分布趋于集中，且各粒径微区间的过滤效率有一定程度的增加.基于滤料试样B的实验发现，以Sauter平均直径D32为基准的过滤效率ED32可以反映不同气液质量比以及不同物理性质的溶液进行喷雾等条件下的过滤效率之间的差异，故可用ED32近似表示过滤介质的综合过滤性能.

（2）通过实验分析计算了纤维过滤介质在容尘阶段的压降Δp与其初始压降Δp0之间的差值（Δp－Δp0）以及各粒径微区间的分级效率随单位面积累计容尘量的变化特性.随着粉尘微粒在纤维滤料表面的沉积，粉尘初层以及最终“树枝状”粉尘层的形成均有助于提高各粒径微区间的分级效率，同时也显著地增加了各容尘阶段的压降值.纤维直径越小的过滤介质，在容尘阶段对各粒径微区间的分级效率越高，随发尘量的增加而增加的速率越快，且增加至100%分级效率所对应的粒径微区间也越小，但其受到的阻力越大，随之带来的运行能耗也越大，而且其容尘量也越小.经分析计算得，用于本文容尘实验的几种纤维滤料在粉尘颗粒沉积的各个压降阶段的最易透过粒径位于［0.184μm，0.407μm］区间内.

（3）经由实验数据分析计算发现，纤维滤料在容尘阶段的填充率与累计容尘量成线性关系（假设单纤维捕集效率取为1），并拟合出两者之间的趋势线关系式.并且，纤维滤料的积尘填充率的变动范围随其容尘量的增大而变宽，随其容尘量的减小而变窄.

（4）分析得到纤维滤料的积尘填充率的计算式，利用实验数据检验了具有代表性的关于非稳态过滤的压降经验公式的适用性，并借助于Matlab的回归分析拟合出合适的压降修正式.

［1］ 陈喆.空气过滤材料及其技术进展［J］.纺织导报，2011，7：86.

CHEN Zhe.Development of air-filter media and its materials［J］.China Textile Leader，2011，7：86.

［2］ CHENG Yuhsiang， TSAI Chuenjinn. Factors influencing pressure drop through a dust cake during filtration［J］.Aerosol Science and Technology，1998，29（4）：315.

［3］ Awni Y Al-Otoom.Prediction of the collection efficiency，the porosity，and the pressure drop across filter cakes in particulate air filtration［J］.Atmospheric Environment，2005，39（1）：51.

［4］ Chikao Kanaoka，Sotoji Hiragi.Pressure drop of air filter with dust load［J］.Journal of Aerosol Science，1990，21（1）：127.

［5］ Thomas D，Penicot P，Contal P，et al.Clogging of fibrous filters by solid aerosol particles experimental and modeling study［J］.Chemical Engineering Science，2001，56（11）：3549.

［6］ Payet S，Boulaud D，Madelaine G，et al.Penetration and pressure drop of a HEPA filter during loading with submicron liquid particles［J］.Journal of Aerosol Science，1992，23（7）：723.

［7］ 罗国华，梁云，郑炽嵩，等.纤维材料过滤理论的研究进展［J］.过滤与分离，2006，16（4）：20.

LUO Guohua，LIANG Yun，ZHENG Chisong，et al.Research progress on filtration theory of fiber materials［J］.Journal of Filtration ＆Separation，2006，16（4）：20.

［8］ 谭天佑，梁凤珍.工业通风除尘技术［M］.北京：中国建筑工业出版社，1984.

TAN Tianyou，LIANG Fengzhen.Industrial ventilation and dust removal technology［M］.Beijing：Chinese Architecture and Building Press，1984.

［9］ 高峰.纤维滤材过滤特性研究［D］.天津：天津大学环境科学与工程学院，2004.

GAO Feng.Research on the filtration characteristic of fibrous material［D］.Tianjin：School of Environmental Science and Engineering of Tianjin University，2004.

［10］ 裘康，焦晓宁，洪贤良，等.非织造布在空气过滤中的应用［J］.产业用纺织品，2005，1：24.

QIU Kang，JIAO Xiaoning，HONG Xianliang，et al.Application of nonwoven fabrics on air filtration［J］.Technical Textiles，2005，1：24.

［11］ 李冶，王伟民.21世纪非织造过滤材料的发展现状及趋势［J］.非织造布，2003，11（1）：13.

LI Ye，WANG Weimin.Development and trend of nonwovens filter materials in 21 century［J］.Nonwovens，2003，11（1）：13.

［12］ 王华英.过滤材料对PM10的过滤性能研究［D］.上海：东华大学环境科学与工程学院，2003.

WANG Huaying.A study of filtration fabric’s purifying performance to PM10［D］.Shanghai：School of Environmental Science and Engineering of Donghua University，2003.

［13］ 吴昌甫.滤清器测试用气溶胶及纤维过滤介质非稳态过滤机理探讨［D］.上海：同济大学机械与能源工程学院，2012.

WU Changfu.Study on the aerosol characteristics and dynamic filtering mechanism of fibrous media based on the test rig for the automotive air-filters［D］.Shanghai：College of Mechanical Engineering of Tongji University，2012.

［14］ Friess H，Yadigaroglu G.Modelling of the resuspension of particle clusters from multilayer aerosol deposits with variable porosity［J］.Journal of Aerosol Science，2002，33（6）：883.

［15］ Japuntich D A，Stenhouse J I T，Liu B Y H.Effective pore diameter and monodisperse particle clogging of fibrous filters［J］.Journal of Aerosol Science，1997，28（1）：147.

［16］ 许钟麟.空气洁净技术原理［M］.上海：同济大学出版社，1998.

XU Zhonglin.Principles of air cleaning technology［M］.Shanghai：Tongji University Press，1998.

［17］ Novick V J，Monson P R，Ellison P E.The effect of solid particle mass loading on the pressure drop of HEPA filters［J］.Journal of Aerosol Science，1992，23（6）：657.

［18］ Davies C N.Air filtration［M］.London and New York：Academic Press，1973.

［19］ Ajay Gupta，Vincent J Novick，Partim Biswas，et al.Effect of humidity and particle hygroscopicity on the mass loading capacity of high efficiency particulate air（HEPA）filters［J］.Aerosol Science and Technology，1993，19（1）：94.

［20］ Yeh Hsuchi，Liu B Y H.Aerosol filtration by fibrous filters—II.experimental［J］.Journal of Aerosol Science，1974，5（2）：205.

［21］ Yeh Hsuchi，Liu B Y H.Aerosol filtration by fibrous filters—I.theoretical［J］.Journal of Aerosol Science，1974，5（2）：191.

［22］ Lee K W，Liu B Y H.Theoretical study of aerosol filtration by fibrous filters［J］.Aerosol Science and Technology，1982，1（2）：147.