高强钢筋混凝土梁短期变形计算方法研究

周建民，陈 硕，王晓锋，赵 勇

（1.同济大学 土木工程学院，上海 200092；2.中国建筑科学研究院，北京 100013）

2011年7月1日，由中国住建部颁布的混凝土结构设计新规范《GB 50010—2010》开始施行，正式将500MPa高强钢筋纳入推广范围.然而，高强钢筋的使用是否会导致正常使用阶段混凝土梁的挠度和裂缝宽度过大，有待进一步论证.我国混凝土规范对钢筋混凝土受弯构件和预应力钢筋混凝土受弯构件分别采用两种不同的模式计算开裂后的刚度，与国际上通行的做法不符；国内外关于刚度的规范公式大多计算复杂，不便于工程实际应用.近年来，同济大学及相关高校根据规范课题组的要求，对配置高强钢筋的混凝土梁和预应力混凝土梁进行了一系列试验，提出了一种精度较高、便于工程应用的高强钢筋混凝土梁短期变形计算的简化方法.

1 试验

1.1 试验概况

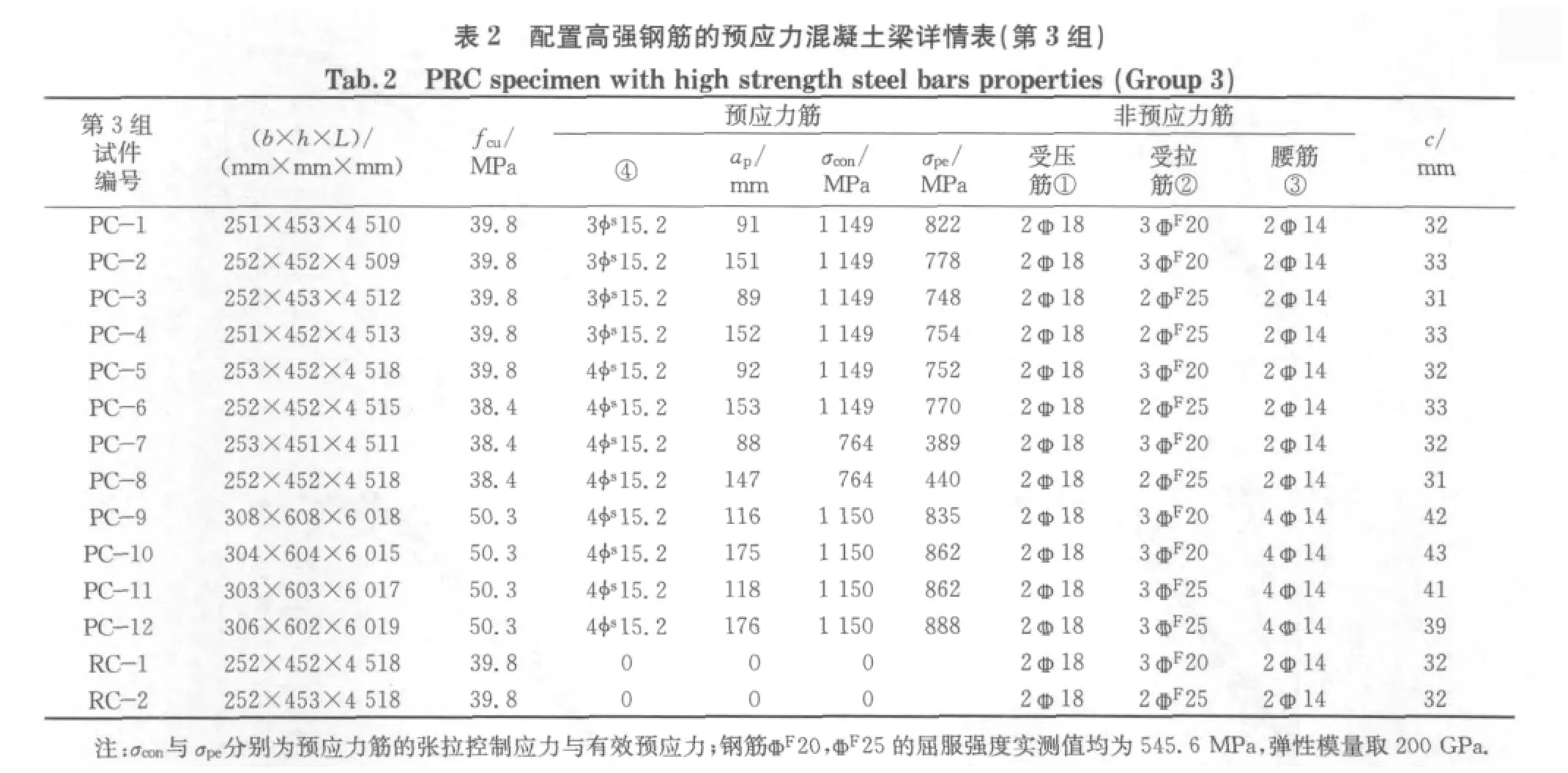
试验采用的加载装置见图1.设计试件综合考虑了以下因素的影响：混凝土强度等级、构件长度、截面尺寸与形式、受拉钢筋面积、混凝土保护层厚度以及预应力效应，具体数值见表1和表2.试件共分3组进行，各组试件的截面形式见图2（其中，第1组为矩形截面，第二组为矩形、T形两种截面，第三组为矩形截面）.前两组均为高强钢筋混凝土梁，反向加载，荷载的施加以纯弯段的设计计算弯矩Mu为参照（相应地，计算极限荷载为Pu），荷载级差为0.1Pu，每级荷载持荷10min，加载至0.9Pu时荷载级差改为0.05Pu直至破坏；第3组为配置高强钢筋的预应力混凝土梁，正向加载，试验梁开裂前荷载级差为0.05Pu，每级荷载持荷30min，试验梁开裂后，荷载级差增至0.1Pu.

图1 试验加载（正向）示意图Fig.1 Positive loading setup

图1中，L为梁的总长；L″为构件边缘至支座的距离，对于第1组取200mm，第2组与第3组取150 mm；L′为剪跨（该区段内配置箍筋），对于第1，2组取（L－2L″）／4，即四分点段，对于第3组取1 200 mm（L＝4 500mm时）或1 650mm（L＝6 000mm时）；L－2L′－2L″为纯弯段（该区段内，第1，2组均不配置箍筋，第3组配置箍筋）.

图2 构件截面示意图Fig.2 Cross section

?

1.2 变形试验结果与分析

?

开始加载时，截面未开裂，试件表现为弹性变形，挠度近似为线性增长；当荷载增至（0.2～0.3）Pu时，纯弯段梁底出现一条或多条裂缝，开裂弯矩试验值与规范计算值符合较好，开裂时应变与挠度均发生突变，表现为荷载－挠度曲线出现明显转折点，随后变形恢复线性增长，且增长幅度大于第一阶段；随着荷载进一步增加，纯弯段裂缝逐渐增多，宽度逐渐加大，开始出现斜裂缝，当荷载增至约（0.4～0.5）Pu（对于预应力梁为0.6Pu）时，裂缝基本出齐，荷载－挠度曲线基本保持为直线；当荷载接近Pu时，混凝土梁中的钢筋与预应力梁中的非预应力筋均进入流塑状态（预应力梁中的钢绞线仍处于弹性状态），荷载－挠度曲线发生第二次明显转折，荷载和挠度均进一步增长直至梁顶混凝土被压碎而破坏.全过程弯矩－跨中挠度曲线基本呈三折线形状，两个转折点分别对应混凝土开裂和高强钢筋受拉屈服的状态.根据试验，混凝土梁与预应力梁跨中混凝土应变基本服从平截面假定，试验梁临近破坏时，受拉钢筋能够达到屈服，故现行混凝土规范中规定的钢筋混凝土受弯构件正截面承载力计算公式仍然适用.

各试件的弯矩－挠度曲线如图3所示（图中，荷载采用相对值，即加载弯矩与极限弯矩之比M／Mu；f为跨中挠度）.可以看出，随着荷载的增加，同一构件的变形迅速增长；截面尺寸相同的试验梁B5F1与B5F2，开裂后其弯矩－挠度曲线出现明显差异，主要原因是配筋率的不同影响着截面有效受压区高度，从而对开裂后的刚度产生影响；配筋率相同的梁CB5-2与CB5-4由于截面尺寸不同（进而初始刚度不同），其弯矩－挠度曲线也不相同；另外，与普通钢筋混凝土梁 CB-1与 CB-2［1］相比，高强钢筋混凝土梁的极限位移与屈服位移之比没有明显降低，但是高强钢筋的配置大大提高了试验梁的极限位移，表现出较为优越的变形性能.由以上分析可知，荷载、配筋率与初始刚度是影响高强钢筋混凝土梁短期变形增长的3个基本因素.

2 短期变形计算方法

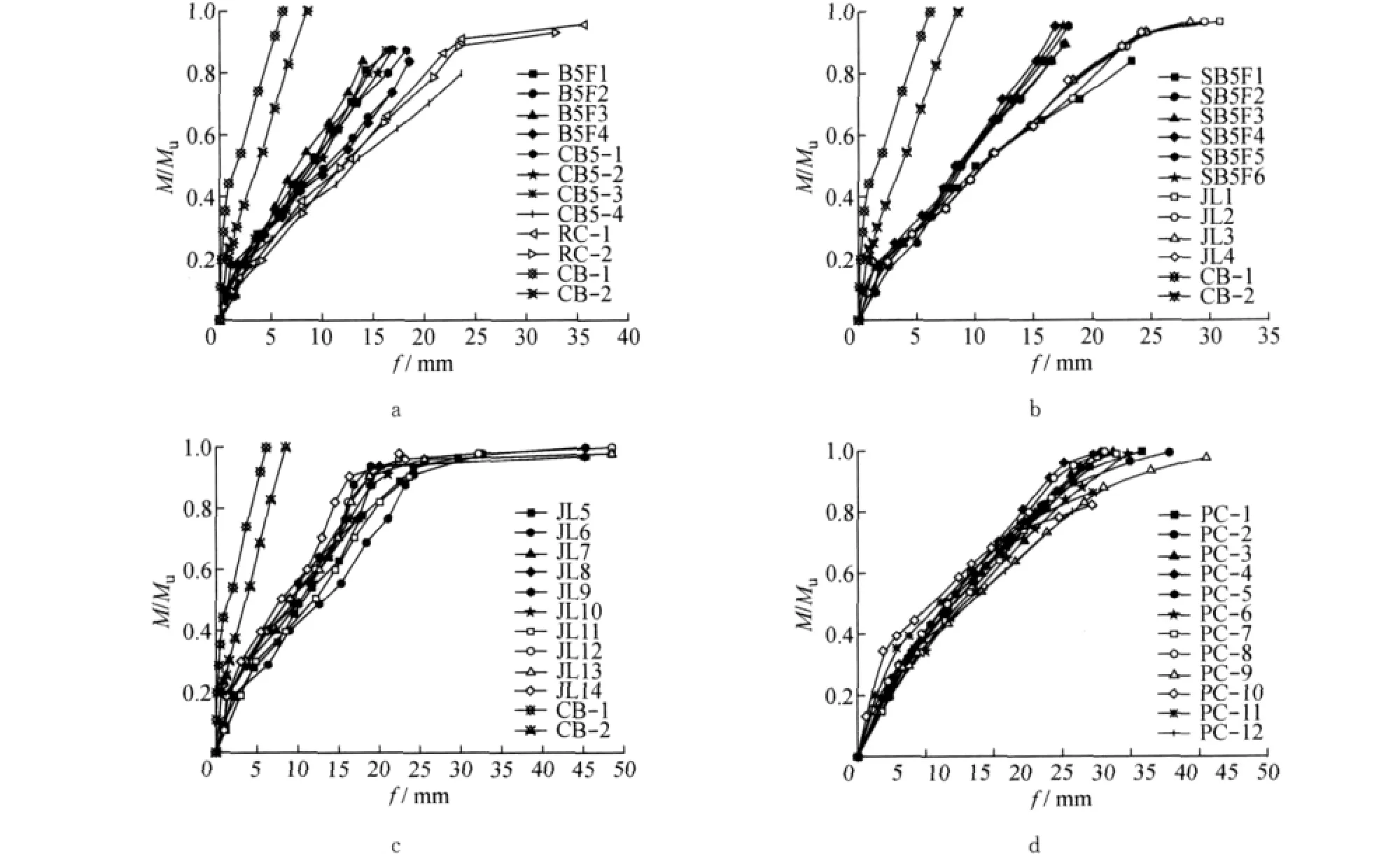
图3 各试验构件M-f曲线汇总Fig.3 Relationship between loading moment and the observed deflection

最小刚度法大致分为三类：解析刚度法（GB 50010—2010）、有效惯性矩法（ACI 318—08）和双直线法（JTG D62—2004，EN 1992-1-1：2004）.现行各混凝土结构设计规范在短期抗弯刚度计算上主要考虑了两方面因素，外部因素为荷载，其变量为Mcr／Mk，其中Mcr，Mk分别为开裂弯矩与使用弯矩；内部因素在开裂前为弹性刚度B0，开裂后为配筋率ρ，这与本文试验得到的结论类似.以下利用B0，ρ，Mcr／Mk推导出混凝土梁与预应力混凝土梁短期抗弯刚度计算的统一公式，并利用试验数据加以验证.

3 统一刚度计算公式的建立

根据试验结果，破坏前混凝土梁纯弯段的弯矩M与曲率φ变化关系可以简化为三个阶段，见图4.第一阶段，作用弯矩小于开裂弯矩，M-φ呈线性关系；构件开裂后，进入第二阶段，M-φ呈近似线性关系，倾斜度小于第一阶段，当配筋率不大时，在该阶段开始点处会出现类似“屈服”的平台；当作用弯矩大于使纵向受拉钢筋屈服的弯矩时，进入第三阶段，M－φ曲线倾斜度继续减小，甚至几乎呈水平状态.

开裂后截面短期平均曲率φs可以表示为

式中：φ0开裂前弹性截面曲率；Δφ为曲率增量.

图4 钢筋屈服前典型弯矩－曲率关系示意图Fig.4 Relationship between moment and curvature before the yielding of the steel

曲率增量Δφ与φcr－φ0近似成正比（φcr为完全开裂截面曲率），并且同M-φ曲线形式有关.当假定构件完全开裂（φ→∞）时，图4中的M-φ曲线将与倾斜的渐近线相交，即Δφ＝φcr－φ0；在一般情况下，Δφ＜φcr－φ0，即Δφ＝ζ（φcr－φ0）（ζ为小于1的折减系数）.试验研究表明，ζ随Mcr／Mk减小而增大，即正常使用弯矩Mk越大，Δφ越大，构件越接近完全开裂的情况；另外，ζ还与配筋率ρ和钢筋与混凝土弹性模量之比（αE＝Es／Ec）的乘积αEρ有关，即比例因子ζ是的函数的具体函数形式可以通过试验结果统计分析得到.则开裂后的短期平均曲率表示为

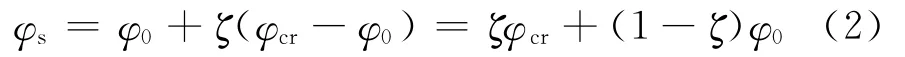
式（2）表明，开裂后截面平均曲率是完全开裂截面曲率φcr与开裂前的弹性截面曲率φ0的加权平均，权数分别为ζ，1－ζ.根据曲率与截面刚度的关系，式（2）可以写成如下形式：

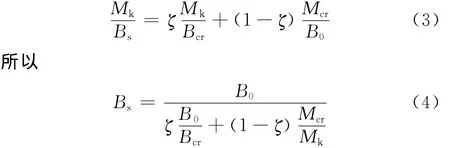
式（4）表明，等效抗弯刚度Bs为B0，Bcr，Mcr／Mk，αEρ的函数.由于开裂截面的刚度Bcr主要与B0，αEρ相关，故实际上Bs只与3个独立变量有关，即Bs＝B（B0，αEρ，Mcr／Mk）或Bs＝B（B0，Bcr，Mcr／Mk）.Bs的具体函数形式可以通过试验结果统计分析得到，或者假定弯矩与曲率为某一个简单函数，对其中参数进行统计分析得到.文献［2］根据弯矩与曲率关系提出的短期刚度近似统一计算式为

本文对式（5）中的参数n进行试算，获得有效刚度的试验值与计算值之比（Bs，t／Bs，c），其均值μ与变异系数δ分别与参数n的关系如图5所示.

图5 Bs，t／Bs，c的数值特征与参数 n 的关系Fig.5 Relationship of Bs，t／Bs，cwith the parameter n

从图5可见，当n≥3时，均值趋近于1，且变异系数差别不大.根据Branson［3］的检验结果，指数取4或者3的相对误差最大为3%，即计算结果对指数取3或者4并不特别敏感.为简化计算，这里取n＝3.此时，均值为0.975，变异系数为0.172，即各数值特征都较理想.于是，式（5）变为

式（6）即为美国ACI 318—08规范采用的刚度计算公式.对式（6）变换，得

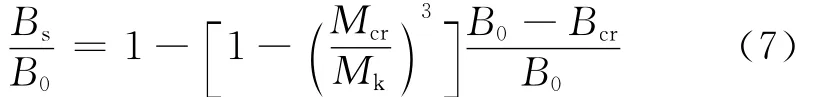
式（7）中Bcr的计算较复杂，其影响因素主要与初始刚度B0和配筋率ρ有关.考虑到钢筋与混凝土弹性模量之比为常数（αE＝Es／Ec），同时为了反映配筋率ρ的影响，这里采用相对刚度形式，即ΔB／B0＝（B0－Bcr）／B0应为αEρ的函数.

式（7）也可以写成如下形式：

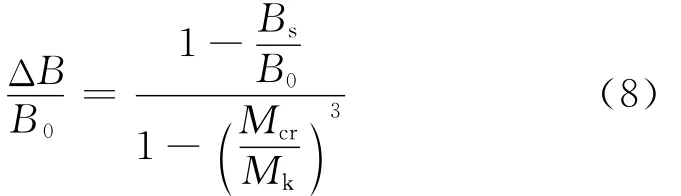
为了得到ΔB／B0与αEρ的数值关系，需要确定两个基本参量：Bs／B0与Mcr／Mk.Bs可通过试验得到，但是鉴于试验成本较高，试验数据有限，也可以用被证实的、具有较高精度的计算公式产生的刚度模拟值来代替.文献［4］建立了滑移、裂缝宽度、刚度相统一的计算公式

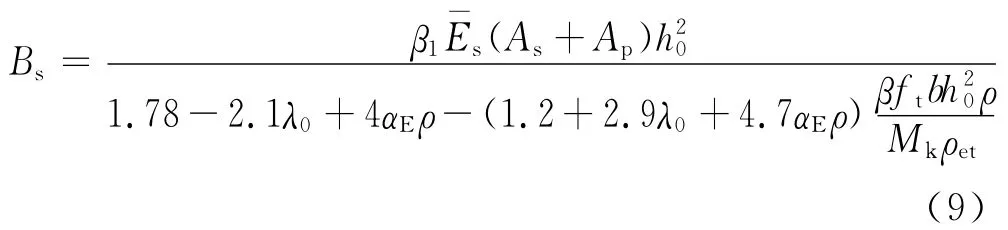
式中：β1为截面形状相关系数为受拉区钢筋平均弹性模量，，对钢筋混凝土梁取分别为普通纵向受拉钢筋、预应力筋的弹性模量；As与Ap分别为普通纵向受拉钢筋、预应力筋的面积；h0为混凝土受压区高度；λ0为预应力度，λ0＝M0／Mk，M0为消压弯矩；ρ＝（As＋Ap）／bh0；ρet＝（As＋Ap）／0.5bh；系数β与钢筋应力、受力形式有关，反映了受拉区混凝土参与工作的程度，0≤β≤0.5；ft为混凝土抗拉强度.公式（9）具有通用性，计算精度高，但计算较为复杂，为此本文按式（8）的模式对该式进一步简化.

考虑到λ0＝M0／Mk＝（Mcr－γftkW0）／Mk＝Mcr／Mk－γftkW0／Mk（γ为截面抵抗矩塑性影响系数，ftk为混凝土抗拉强度，W0为截面受拉边缘弹性抵抗矩），而γftkW0／Mk相当于无预应力混凝土时的Mcr／Mk，由于预应力的影响，该项占预应力混凝土梁中Mcr／Mk的比例较小.同济大学已有的试验梁计算结果表明，γftkW0／Mk约为0.11～0.17，取γftkW0／Mk≈0.15，则λ0＝Mcr／Mk－0.15.同时，为简化计算，系数β取为0.25.

公式（9）表明，Bs为配筋率ρ的函数（当Mcr／Mk确定后ftbh20／Mk为常数），实际上由ACI规范也有相同结论.故通过对Mcr／Mk赋值，利用式（9）可以得到ΔB／B0与αEρ的确定关系.对于配置高强钢筋的混凝土梁，经济配筋率ρ一般在0.6%～1.5%之间.取正常使用弯矩Mk≈（0.60～0.80）Mu，则混凝土梁Mcr／Mk≈0.12～0.50（相应地，Mcr／Mu≈0.1～0.3）；预应力混凝土梁取Mcr／Mk≈0.25～0.65（相应地，Mcr／Mu≈0.20～0.40）.计算结果见图6与图7.

图6 高强钢筋混凝土梁ΔB／B0－αEρ曲线Fig.6 ΔB／B0－αEρcurve of RC beam with high strength steel bars

从图6与图7可以看出，ΔB／B0与αEρ基本呈线性关系；预应力梁与普通高强钢筋混凝土梁的拟合结果差别不大.现对两种情况下的均值拟合公式再进行一次平均运算，并微调取整后得到以下公式：

图7 高强钢筋预应力混凝土梁ΔB／B0－αEρ曲线Fig.7 ΔB／B0－αEρcurve of PRC beam with high strength steel bars

将式（10）代入式（8），即得到高强钢筋混凝土梁短期抗弯刚度统一计算模式

4 计算公式的验证

为了验证式（11），除本文试验数据以外，还收集整理了国内其他高校相关试验结果［1，5－18］.表3为试验挠度 与 计 算 挠 度 之 比 （fs，t／fs，c）的 统 计 结 果，其中，μ为均值，δ为变异系数.为了比较，本文也给出了由 GB 50010—2010，ACI 318—08，JTG D62—2004，EN 1992-1-1：2004等规范公式以及式（9）得到的计算结果.

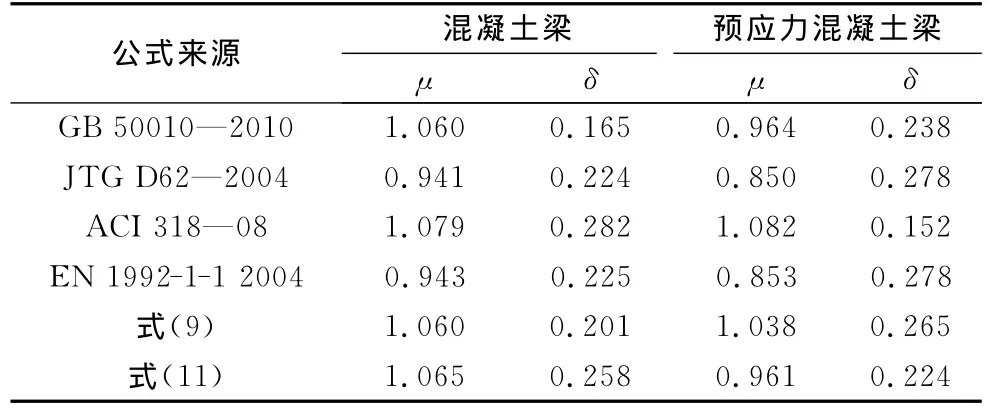
表3 各公式（fs，t／fs，c）计算精度对比Tab.3 Comparison of calculation results（fs，t／fs，c）

从表3可以看出，根据国内公路桥涵规范和欧洲规范计算得到的挠度对于普通混凝土梁和预应力混凝土梁都明显偏大，按中国GB 50010—2010规范、美国ACI 318—08规范、文献［4］和式（11）计算出的结果与试验值比较接近，表明现行新规范适用于高强钢筋混凝土部分.无论是美国ACI 318—08规范公式，还是文献［4］提出的公式其计算都比较复杂，物理概念不够直观.本文建议公式对预应力混凝土梁和钢筋混凝土梁采用统一的表达式，不仅计算精度较高，而且形式简单，其物理概念也十分明确，反映了影响刚度的主要因素.

5 结论

（1）对配置500MPa钢筋的混凝土梁与预应力混凝土梁的试验结果表明，混凝土梁的挠度主要与荷载、配筋率、初始刚度有关；同时，新规范 GB 50010—2010对配置高强钢筋的混凝土梁在短期挠度计算上是适用的.

（2）基于混凝土梁抗弯刚度与裂缝宽度计算的统一模式，推导出钢筋混凝土梁短期变形计算的简化建议式.

（3）将建议公式与国内外规范在变形计算上的精度进行对比，结果表明，建议公式不仅适用于高强钢筋混凝土梁，也适用于预应力混凝土梁，而且计算精度高，形式简单，物理含义明确，工程应用性强.

［1］ 丁振坤，邱洪兴，胡涛，等.HRB500级钢筋混凝土梁受弯刚度试验［J］.建筑科学与工程学报，2009，26（1）：115.

DING Zhenkun，QIU Hongxing，HU Tao，et al.Experiment on flexural stiffness of reinforced concrete beams with HRB500 reinforcement bars［J］.Journal of Architecture and Civil Engineering，2009，26（1）：115.

［2］ 白生翔，王晓锋.混凝土受弯构件短期弯曲刚度统一模式［C］／／第十四届全国混凝土及预应力混凝土学术会议论文.长沙：中国土木工程学会，2007：312-318.

BAI Shengxiang，WANG Xiaofeng.A unified model for shortterm flexural stiffness of concrete bending members［C］／／The 14th National Concrete and Prestressed Concrete Conference.Changsha：China Civil Engineering Society，2007：312-318.

［3］ Dan Earle Branson.Deformation of concrete structures［M］.New York：McGraw-Hill，1976.

［4］ 周建民，朱军，朱顺宪.混凝土梁裂缝宽度、刚度的统一计算方法及应用［J］.铁道学报，2000，22：62.

ZHOU Jianmin，ZHU Jun，ZHU Shunxian.A unified computing model for the crack width and the flexural stiffness in concrete members and its application［J］.Journal of The China Railway Society，2000，22：62.

［5］ 丁振坤.混凝土受弯构件抗弯刚度计算方法研究［D］.南京：东南大学土木工程学院，2008.

DING Zhenkun.Study on flexural stiffness calculation method of concrete members［D］.Nanjing：School of Civil Engineering of Southeast University，2008.

［6］ 蒋永生，梁书亭，陈德文，等.高强钢筋高强混凝土受弯构件的变形性能试验研究［J］.建筑结构学报，1998，19（2）：37.

JIANG Yongsheng，LIANG Shuting，CHEN Dewen，et al.Experiment research for deformation behavior of high-strength flexural member with high-strength rebars［J］.Journal of Building Structures，1998，19（2）：37.

［7］ 李艳艳.配置500 MPa钢筋的混凝土梁受力性能的试验研究［D］.天津：天津大学建筑工程学院，2007.

LI Yanyan.Experiment research on behaviors of reinforced concrete beams with 500MPa steel bars［D］.Tianjin：School of Civil Engineering of Tianjin University，2007.

［8］ 肖红菊.HRB400级钢筋混凝土梁受弯性能研究［D］.郑州：郑州大学土木工程学院，2006.

XIAO Hongju.Experiment research on the bend behavior of HRB400 reinforced concrete beams［D］.Zhengzhou：School of Civil Engineering of Zhengzhou University，2006.

［9］ 李美云.HRB400级钢筋混凝土构件受力性能的试验研究［D］.郑州：郑州大学土木工程学院，2003.

LI Meiyun.The study of the mechanical property of HRB400 reinforced concrete members［D］.Zhengzhou：School of Civil Engineering of Zhengzhou University，2003.

［10］ 张艇.HRB500级钢筋混凝土构件受力性能的试验研究［D］.郑州：郑州大学土木工程学院，2004.

ZHANG Ting.The study of the mechanical property of HRB500 reinforced concrete members［D］.Zhengzhou：School of Civil Engineering of Zhengzhou University，2004.

［11］ 王全凤，刘凤谊，杨勇新，等.HRB500级钢筋混凝土简支梁受弯试验［J］.华侨大学学报，2007，28（3）：300.

WANG Quanfeng，LIU Fengyi，YANG Yongxin，et al.Experimental investigation on flexural behavior of simple supported RC beams with grade HRB500 reinforcement［J］.Journal of Huaqiao University，2007，28（3）：300.

［12］ 于秋波，刘立新，胡丹丹，等.HRB500级钢筋部分预应力混凝土梁受力性能的试验研究［J］.建筑结构，2009，39：527.

YU Qiubo，LIU Lixin，HU Dandan，et al.Experiment study on flexural behavior of prestressed concrete beams using the HRB500 steel bars as nonprestressed reinforcement［J］.Building Structure，2009，39：527.

［13］ 于秋波，刘立新，谢丽丽，等.HRB500级钢筋用于先张预应力梁的非预应力筋试验研究［J］.四川建筑科学研究，2009，35（1）：6.

YU Qiubo，LIU Lixin，XIE Lili，et al.Experiment research of the prestressed concrete structure behavior with HRB500 steel bars［J］.Sichuan Buiding Science，2009，5（1）：6.

［14］ 于秋波.HRB500级钢筋部分预应力混凝土梁受力性能研究［D］.郑州：郑州大学土木工程学院，2008.

YU Qiubo.Study on stress behavior of partially prestressed concrete beams with HRB500 steel bars［D］.Zhengzhou：School of Civil Engineering of Zhengzhou University，2008.

［15］ 冯辉.配HRB500级钢筋后张法预应力混凝土梁受力性能的研究［D］.郑州：郑州大学土木工程学院，2007.

FENG Hui.The study about the mechanical property of posttensioned prestressed flexural members with HRB500 steel bars［D］.Zhengzhou：School of Civil Engineering of Zhengzhou University，2007.

［16］ 胡丹丹.配500 MPa钢筋折线先张法预应力混凝土梁受力性能的研究［D］.郑州：郑州大学土木工程学院，2007.

HU Dandan：The experiment of research on fold-line pretension pre-stressed beam with 500 MPa high strength steel bars［D］.Zhengzhou：School of Civil Engineering of Zhengzhou University，2007.

［17］ 杜毛毛，苏小卒，赵勇.配500 MPa钢筋后张有粘结预应力混凝土梁受弯试验［J］.沈阳建筑大学学报，2009，25（2）：211.

DU Maomao，SU Xiaozu，ZHAO Yong.Flexural test of posttensioned bonded prestressed concrete beams with 500MPa steel bars［J］.Journal of Shenyang Jianzhu University，2009，25（2）：211.

［18］ 张利梅，赵顺波，黄承逵.高性能预应力混凝土梁挠度试验与计算方法［J］.大连理工大学学报，2005，45（1）：96.

ZHANG Limei， ZHAO Shunbo， HUANG Chengkui.Experimentation and calculation of deflection of prestressed high-performed concrete beams ［J］. Journal of Dalian University of Technology，2005，45（1）：96.