跃移雪颗粒运动特性的数值模拟研究
周晅毅,刘长卿,顾 明
(同济大学 土木工程防灾国家重点实验室,上海 200092)
风致积雪运动的基本过程按雪粒离开地面的程度分为蠕移、跃移及悬移运动,许多学者认为,跃移运动对雪颗粒的迁移有很大的贡献.研究风致积雪运动的方法大致分为4类:理论分析、实地观测、风洞试验和数值模拟.数值模拟方法因其成本低,周期短,可以方便地改变各种参数来研究其对结果的影响规律,越来越受到雪工程研究人员的关注.
近年来,计算流体力学方法在气固两相流的数值模拟中应用越来越广,受到不同行业学者的关注[1-2].Uematsu,Naaim 和 Beyers等人都曾致力于风雪运动的数值模拟研究.Uematsu等将雪颗粒跃移和悬移考虑在模型中,提出了跃移层风雪流输运质量方程[3];Naaim等构建了雪粒堆积和风蚀模型来描述雪表面和风雪流之间的质量交换[4];Gordon等通过实地观测,得到了雪颗粒形状、粒径等分布情况[5];Beyers等人结合实测数据,讨论了雪颗粒沉积和侵蚀对雪运动的影响[6];X.Y.Zhou等采用两相流理论模拟风吹雪运动,在计算流体动力学软件FLUENT的平台上进行了二次开发,对北京首都机场T3航站楼屋面的雪荷载分布规律进行了分析,为结构设计提供了依据[7];周晅毅等在考察雪颗粒运动机理的基础上,采用RANS方法对无建筑开阔场地的风雪流进行了模拟,并与经典文献中的实测结果进行了对比[8].以上学者的研究都是采用欧拉-欧拉方法,即把雪相和空气相都假定为连续相处理;黄宁等采用欧拉-拉格朗日方法对风沙(雪)运动进行研究[9-11],即把固相认为是离散介质,其方法对风雪流的研究有着借鉴意义.
本文基于雪颗粒跃移质量传输率等相关的经验公式,建立了雪面侵蚀质量通量与粒子跃移数目之间的关系,结合拉格朗日方法,分析了研究粒子起跳速度、粒子直径和摩擦速度等参数对运动轨迹的影响.在此基础上,对雪颗粒质量传输率进行了计算,并与已有的经验公式进行比对分析,验证了本文提出的假设和计算方法的合理性和有效性.
1 理论分析
1.1 跃移质量传输率定义
雪跃移质量传输率,是指单位时间跃移层内单位宽度通过的雪的质量(kg·m-1·s-1),即
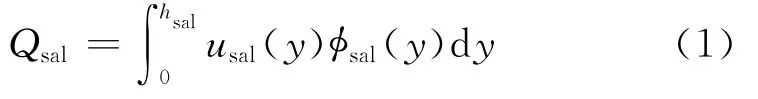
式中:hsal表示雪颗粒的跃移高度;usal(y)表示y高度处雪颗粒跃移水平平均速度;φsal(y)表示y高度处雪跃移的浓度,即跃移层中y高度处单位体积内雪的质量.usal(y),φsal(y)都随高度变化,需将两者乘积沿高度积分才能获得Qsal.
1.2 雪跃移量经验公式
质量传输率作为描述雪颗粒跃移的重要参数,很多学者都曾经做过大量的研究工作,提出了相关的经验公式.其中,对于空旷环境下的雪颗粒传输率计算,Iversen与Pomeroy的经验公式应用十分广泛.
Iversen假定跃移雪颗粒的起动速度与(u*-u*t)相关,给出跃移雪质量传输率的经验公式[12]为
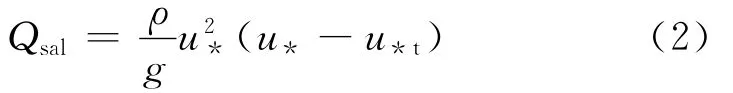
式中:ρ为空气密度;g为重力加速度,取为9.8m·s-2;u*为壁面摩擦速度;u*t为阈值摩擦速度.
Pomeroy结合平坦流域雪跃移的实测数据,给出雪跃移质量传输率的经验公式[13]为
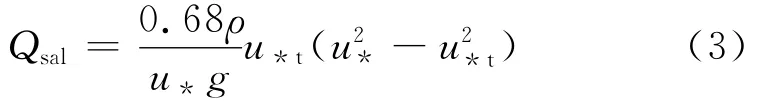
1.3 雪侵蚀量经验公式
雪是否发生侵蚀或沉积由近壁面的摩擦速度(风速)决定.当摩擦速度u*超过阈值摩擦速度u*t,壁面上的雪被风吹起,即发生侵蚀.雪侵蚀量(即质量通量,kg·m-2·s-1)可用下式表达[6]:
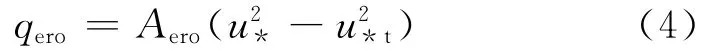
式中:Aero为常系数,取Aero=7×10-4.
此外,还有其他学者,如Uemastu提出经验公式[3]为
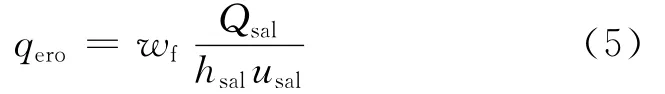
式中:wf为粒子下落速度;usal为粒子跃移速度;usal=2.8u*t;hsal为粒子平均跃移高度,可用下式表达[13]:

2 跃移雪颗粒运动模型
2.1 雪颗粒受力分析
雪颗粒在气流中受力较多,例如气动升力、Saffman力、Magnuss力等,但并不是每一种力在运动分析时都需要考虑.同时,考虑到重力、阻力和浮力是雪颗粒运动的主要驱动力,后续的分析都近似忽略其他外力的作用.
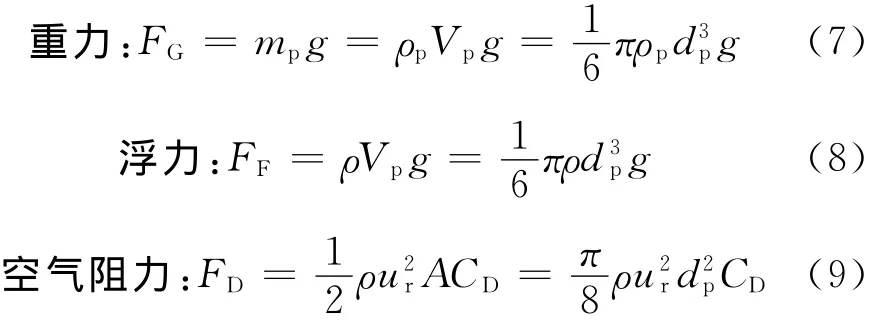
式(7)~(9)中:mp为雪颗粒质量;ρp为雪颗粒密度;Vp为雪颗粒体积;dp为雪颗粒直径;ur为雪颗粒与空气的相对速度;A为雪颗粒迎风面横截面面积;CD为阻力系数,采用经验公式[14]Re),Re为颗粒雷诺数.
前文所述的粒子下落速度wf按照文献经验公式[15]取为,将CD与Re的表达式代入其中,下落速度可变换为
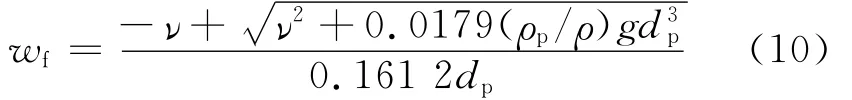
式中:ν为空气的运动黏性系数.
可见,下落速度是雪颗粒密度及直径的函数,如图1所示,随着雪颗粒粒径和密度的增大,下落速度也随之增大.
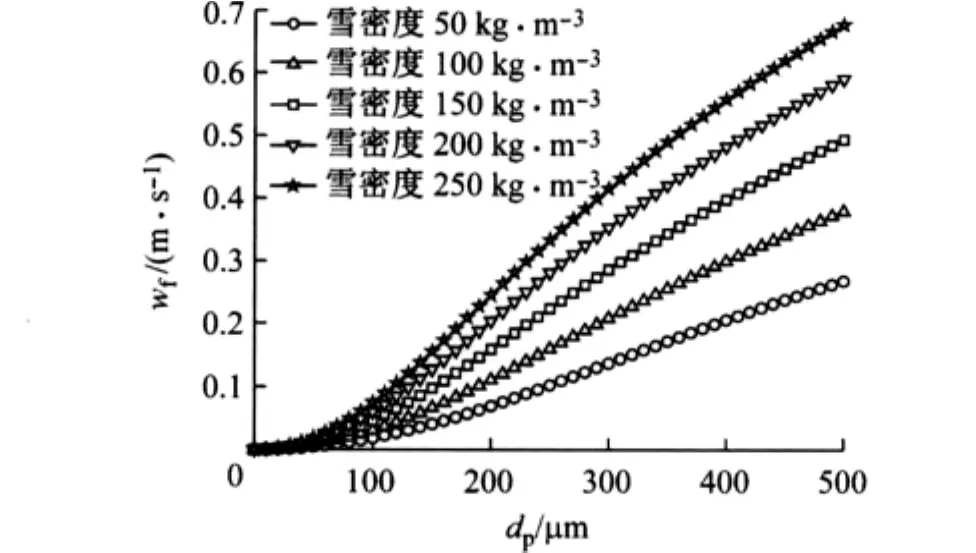
图1 雪颗粒下落速度变化规律Fig.1 Settling velocity as a function of snow particle diameter
2.2 雪颗粒竖向起跳速度分布函数
假定在跃移运动中,雪颗粒全部为垂直起跳.当颗粒以不同速度起跳时,记竖向初速度分布函数为f(v0),即单位时间从单位面积上起跳的颗粒中,以速度v0起跳的粒子数目与颗粒总数之比为f(v0).采用Anderson and Hallet提出的如下指数函数形式的初速度分布[16],见图2.
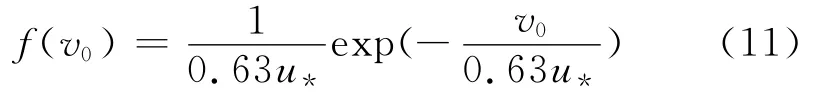
观察图2,在同一摩擦速度下,以较小速度起跳的雪粒的概率比较大,并且随着雪粒起跳速度的增大,相应的概率逐渐减小.随着摩擦速度增大,以较小速度起跳的雪粒的概率较低,以较大速度起跳的雪粒的概率变大.
2.3 雪颗粒运动方程
经过上述受力分析,把粒子运动简化为二维平面运动,通过坐标与时间(x,y,t)表示,运动轨迹方程为
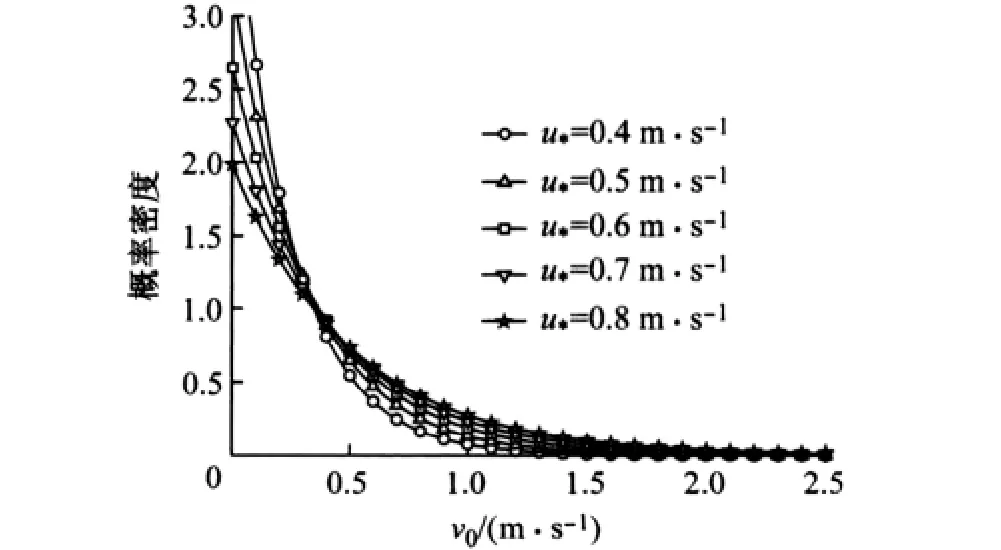
图2 颗粒竖向起跳速度概率密度分布Fig.2 Probability distribution of liftoff velocity of particles
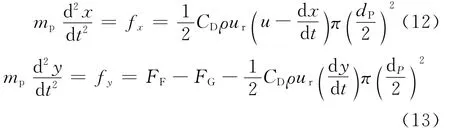
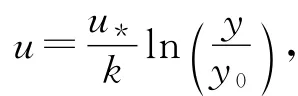
3 雪颗粒运动轨迹计算分析
3.1 跃移轨迹与雪颗粒粒径关系
由上述运动方程(12),(13)可知,影响雪颗粒运动轨迹的参数因素包括粒子的直径、密度和摩擦速度等因素.表1给出了我国天山地区积雪参数的大致范围[17].可见,雪颗粒的直径大约为毫米量级,而雪颗粒的密度大约为40~300kg·m-3不等.

表1 我国新疆天山地区积雪参数Tab.1 Snow parameters of Tianshan region in Xinjiang Uygur Autonomous Region of China
给定雪颗粒运动的初始条件:假定粒子的初始坐标为(0,0.005),初始速度只有竖向速度,水平速度为零,具体见表2.运动方程(12),(13)便可通过龙格-库塔方法进行求解,得到雪颗粒的运行轨迹.如无特殊说明,本文的计算按表2中取值.
在同等摩擦速度(u*=0.5m·s-1)条件下,粒子起跳速度分别为0.5m·s-1和2.0m·s-1时,分别绘出粒子直径为0.30,0.45,0.60与0.75mm 的颗粒运行轨迹.从图3可得,在相同的起跳速度时,随着粒子直径的增大,粒子的跃移高度h逐渐变大;并且,由图3a与3b对比可知,随着粒子初始速度增大,其所能达到的最大跃移高度也随之增大.例如,当起跳速度由0.5m·s-1增加到2.0m·s-1时,粒径为0.45mm的颗粒的最大跃移高度由0.014m增加到0.053m.另外,观察图3,当颗粒起跳速度不同时,水平跃移距离l的变化规律是相反的:图3a中,粒子起跳速度较小时,随着粒子直径的增大,粒子的跃移长度逐渐变小;而图3b中,粒子起跳速度较大时,随着粒子直径的增大,粒子的跃移长度逐渐变大.阻力占竖向力中的比例相对较小,故跃移高度较大.因此,在物理意义上,图3中的现象便得到了合理的解释.而且,这与文献[18]的计算结论是类似的,在一定程度上也验证了本文计算结果的准确性.

表2 数值计算的相关参数Tab.2 Numerical calculation related parameters
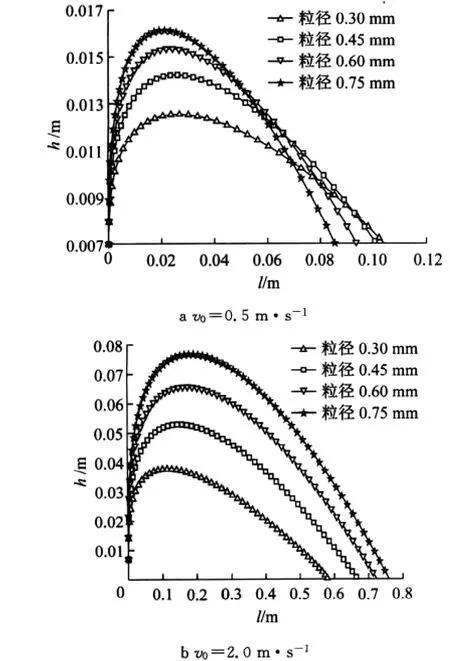
图3 雪颗粒跃移轨迹随直径的变化规律Fig.3 Saltation trajectory as a function of snow particle diameter
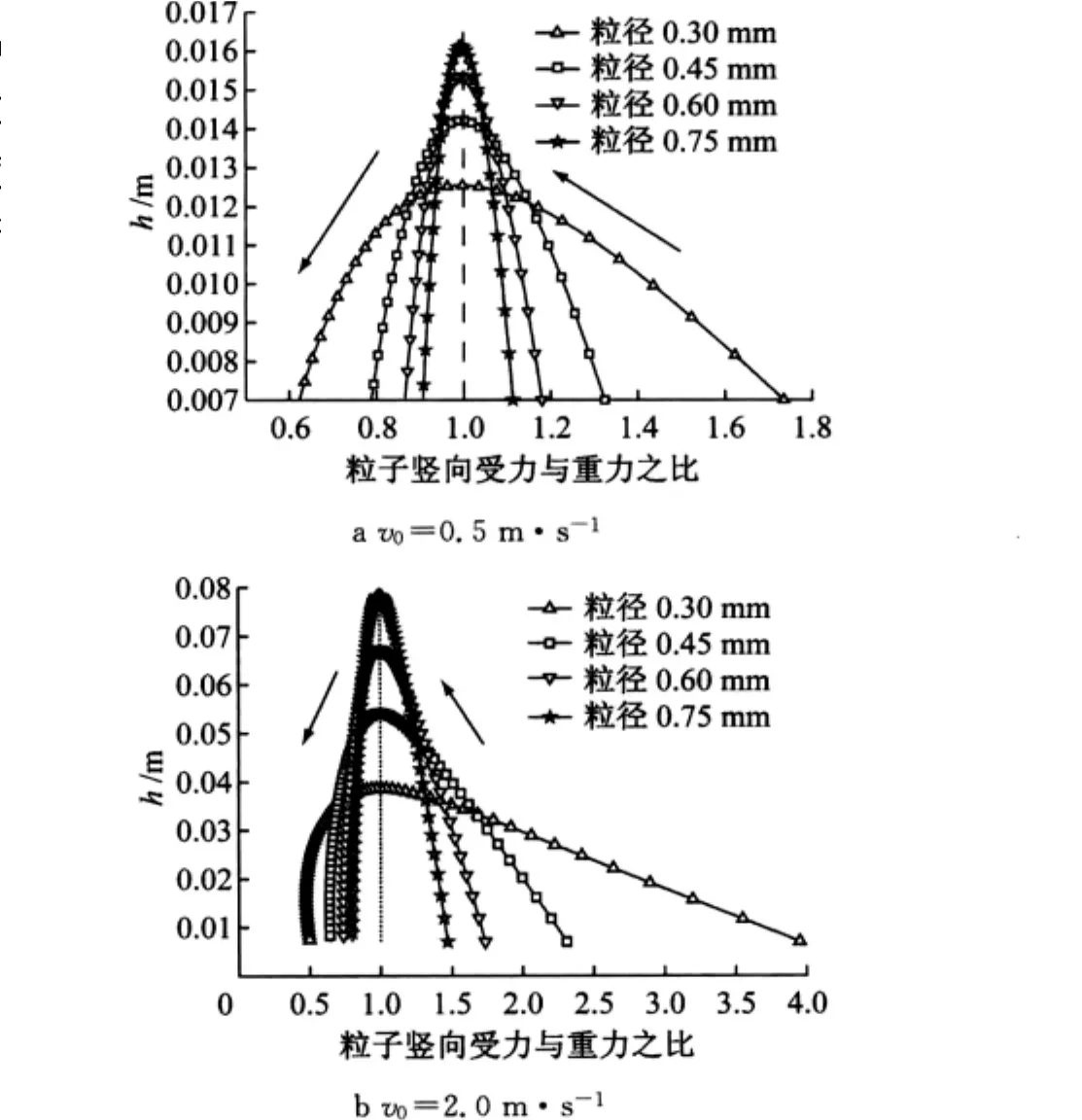
图4 雪颗粒竖向受力与重力之比随跃移高度的变化曲线Fig.4 Variation curves of the ratio of vertical force to gravity with saltation height
图4中箭头↑、↓分别表示粒子处于上升和下降阶段.通过前文的受力分析可知,粒子在上升过程中,重力和空气阻力竖向分量方向均向下.在粒子达到最大跃移高度处,粒子只有水平方向的速度,空气阻力的竖向分量为零,雪颗粒在竖直方向只受到重力的作用(浮力相比较小),此时竖向受力与重力之比为1.不难发现,在上升过程中,当粒子以相同的速度起跳时,由于空气阻力起减速作用,较小粒径的雪颗粒受到的空气阻力占竖向力中的比例较大,因而最大跃移高度较小;而较大粒径雪颗粒受到的空气
图5所示为雪颗粒水平受力与重力之比随跃移高度的变化规律.图中横坐标轴的正负号表示水平受力的方向,“+”表示起加速作用,“-”表示起减速作用.图5a中,粒子的粒径越小,其水平方向受力与重力之比越大,且图5a中水平力几乎都为正值,即当粒子起跳速度较小时,在运动过程中,粒子速度一直小于风速,水平作用力起加速作用,故而小粒径的雪颗粒跃移长度较大;图5b中,下降阶段,水平力为负值,即当粒子起跳速度较大时,在下降过程中,粒子速度一直大于风速,水平作用力起减速作用.且粒径越小,受到的阻力越大,故小粒径的雪颗粒的跃移距离可能会小一些.当然,由于本文对雪颗粒做了球体的假设,这样的结论尚需进一步的验证.
3.2 跃移轨迹与摩擦速度关系
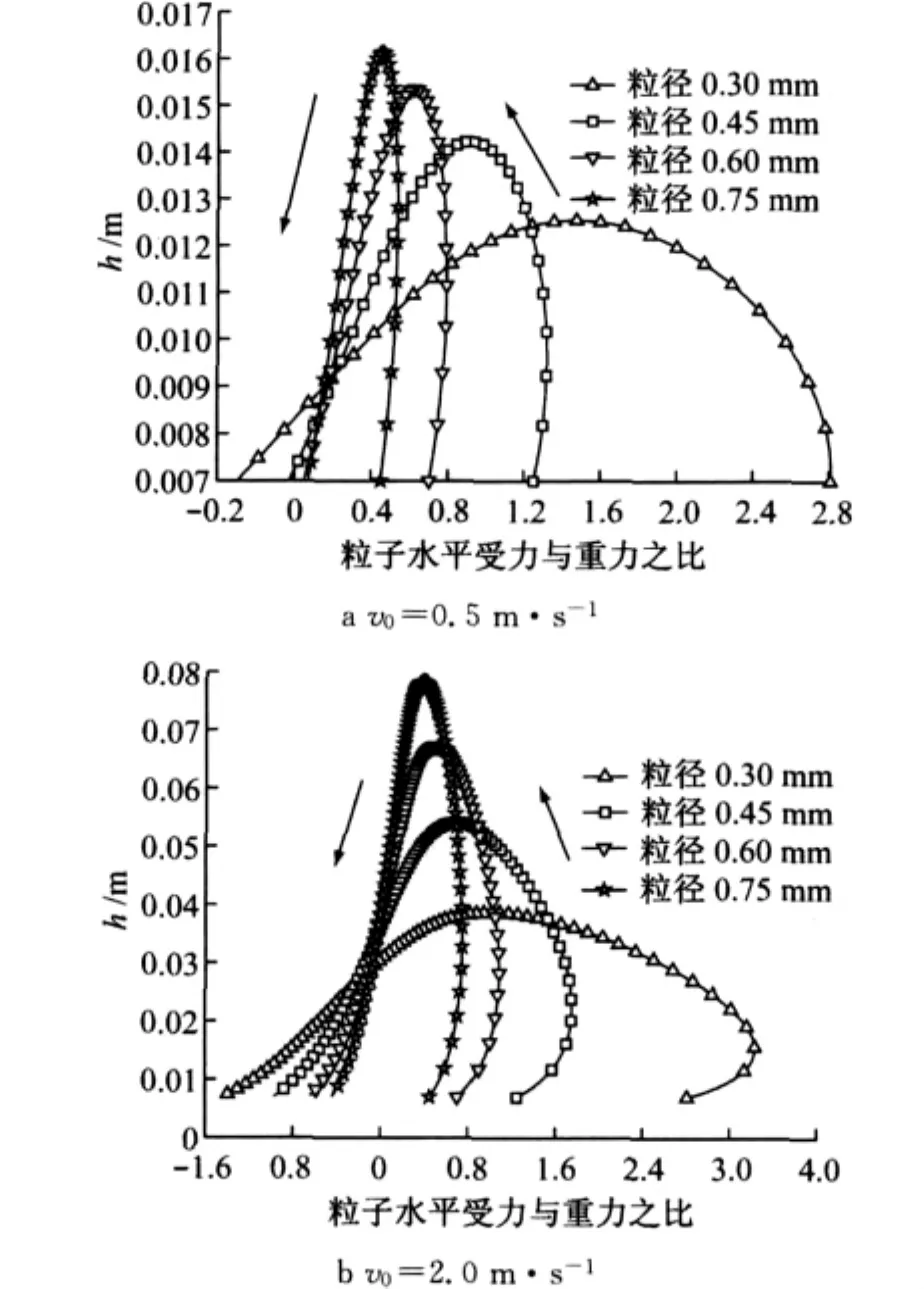
图5 雪颗粒水平受力与重力之比随跃移高度的变化曲线Fig.5 Variation curves of the ratio of horizontal force to gravity with saltation height
不同粒径的颗粒最大水平跃移距离(即跃移长度)随摩擦速度的变化规律如图6所示.与前文3.1类似,粒子起跳速度不同时,水平跃移距离的变化规律也不同.当颗粒起跳速度较小时,如图6a中,v0=0.5m·s-1,随着摩擦速度的增大,颗粒的水平跃移距离先增大后减小;且随着粒子直径的增大,水平跃移距离随之减小.当颗粒起跳速度较大时,如图6b中,v0=2.0m·s-1,随着摩擦速度的增大,不同粒径颗粒的水平跃移距离都随之增大,但增大的幅度不同.较小粒径的颗粒水平跃移距离随着摩擦速度的增大幅度相比粒径较大的颗粒增幅小一些.例如对于粒径为0.15mm的颗粒,当摩擦速度从0.2m·s-1增加到1.0m·s-1时,水平跃移距离的增大幅度为0.21mm;而对于粒径为0.75mm的颗粒,当摩擦速度从0.2m·s-1增加到1.0m·s-1时,水平跃移距离的增大幅度为0.44mm,约为前者的2.1倍.
上述现象的具体原因,可由图7中所描述的变化规律予以解释.由于篇幅所限,数据较多,且变化规律类似,图中只列举了一些代表性的摩擦速度数值下的变化规律(颗粒直径为0.45mm).例如图7a中,当粒子起跳速度较小时,在上升阶段,此时粒子速度小于风速,水平作用力起加速作用.当摩擦速度u*小于0.5m·s-1时,随着摩擦速度的增大,粒子在水平方向的受力与重力之比随之变大,在u*=0.5m·s-1时,水平受力与重力之比最大;当摩擦速度u*大于0.5m·s-1时,随着摩擦速度的增大,粒子在水平方向的受力与重力之比随之变小.这就解释了图6a中跃移长度先增大后减小,且在0.5m·s-1时其跃移长度最大的原因.图7b中,起跳速度为2.0m·s-1与起跳速度为0.5m·s-1的跃移规律明显不同,在上升阶段,随着摩擦速度的增大,粒子在水平方向的受力与重力之比随之变大.因而当竖向起跳速度较大时,摩擦速度增大,水平跃移长度增加.
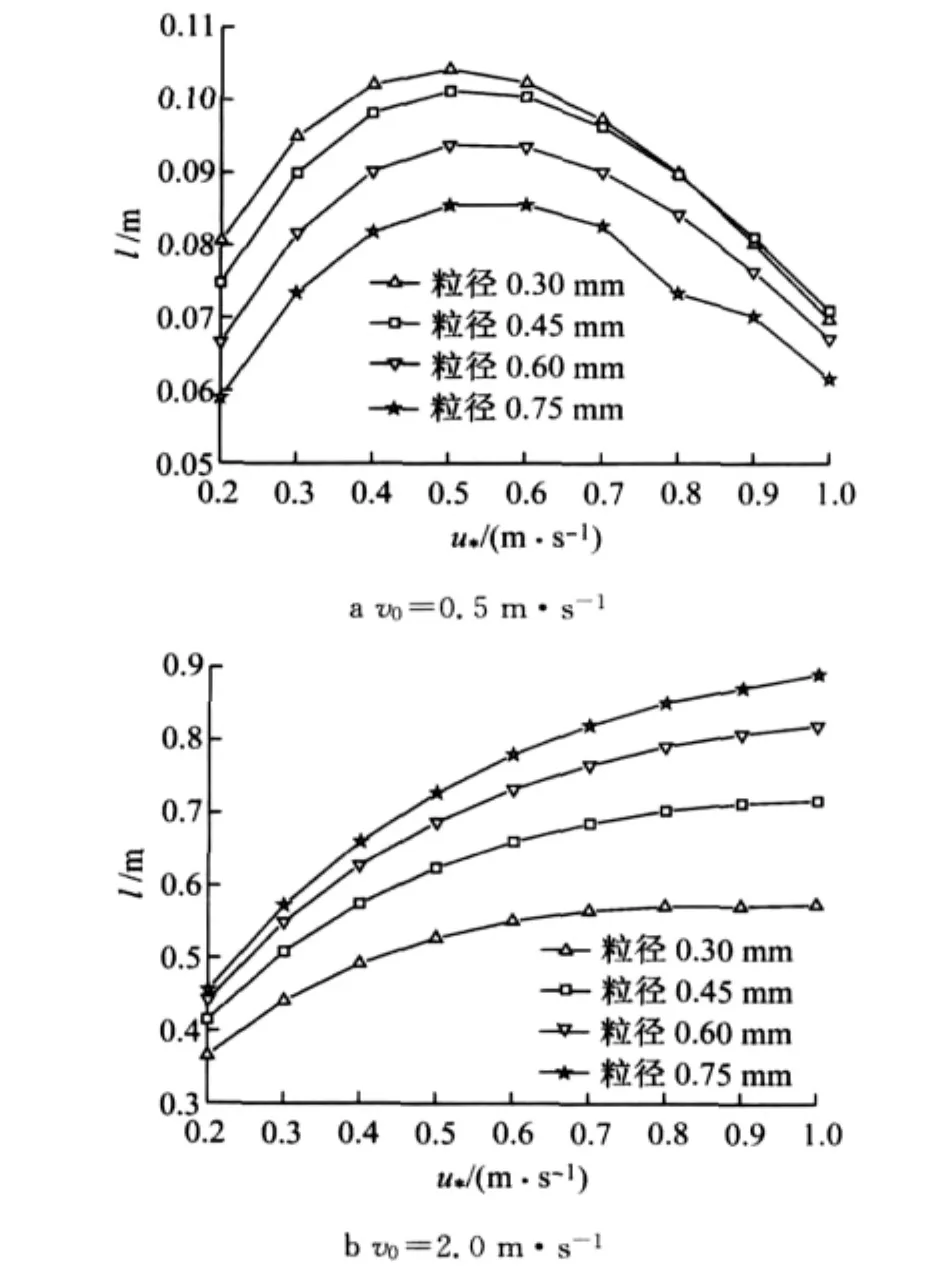
图6 水平跃移距离随摩擦速度的变化曲线Fig.6 Variation curves of saltation length with friction velocity
由图8可知,在粒径不变的情况下,随着摩擦速度的增大,本文所计算出的跃移高度并未发生明显的变化,基本维持在某一固定值附近;而经验公式中,跃移高度与摩擦速度呈抛物线关系.可以看出,本文计算出的粒子跃移高度介于平均跃移高度hsal最大值与最小值的范围之内,并且随着起跳速度的增大而增大.一方面说明了传统经验公式的合理性,另一方面也进一步验证了本文计算的粒子跃移轨迹的有效性.
3.3 跃移轨迹与雪颗粒密度关系
假定雪颗粒粒径单一不变,均为0.45mm,颗粒跃移轨迹与雪颗粒密度的变化关系如图9所示.可见,随着雪颗粒密度的增大,粒子的跃移高度随之增大.
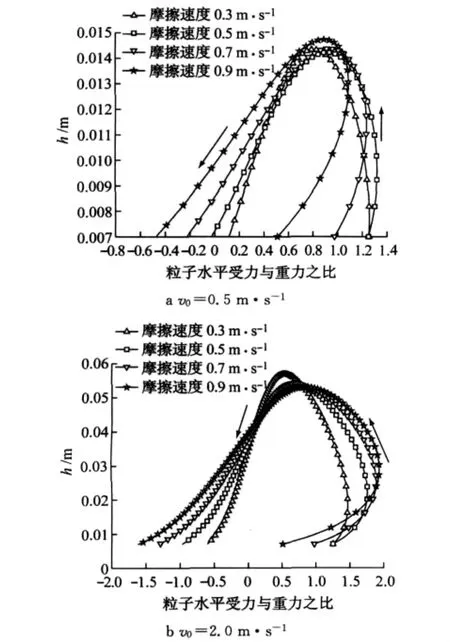
图7 雪颗粒水平受力与重力之比随跃移高度的变化曲线(粒径0.45mm)Fig.7 Variation curves of the ratio of horizontal force to gravity with saltation height(d=0.45mm)
对比图4和图10,通过前文的受力分析可知,粒子在上升过程中,空气阻力竖向分量向下,在粒子达到最大跃移高度处,粒子只有水平方向的速度,空气阻力的竖向分量为零,雪颗粒在竖直方向只受到重力的作用(浮力相比较小).此时,竖向加速度近似等于重力加速度g.在上升过程中,粒子做减速运动,加速度越大,上升的高度越低.由图10可知,竖向起跳速度相同时,较小密度的雪颗粒竖向加速度较大,因而最大跃移高度较低;而较大密度的颗粒的加速度相对较小,故跃移高度较大.这与前文3.1的变化规律类似.
4 雪颗粒跃移质量传输率计算分析
4.1 本文计算模型
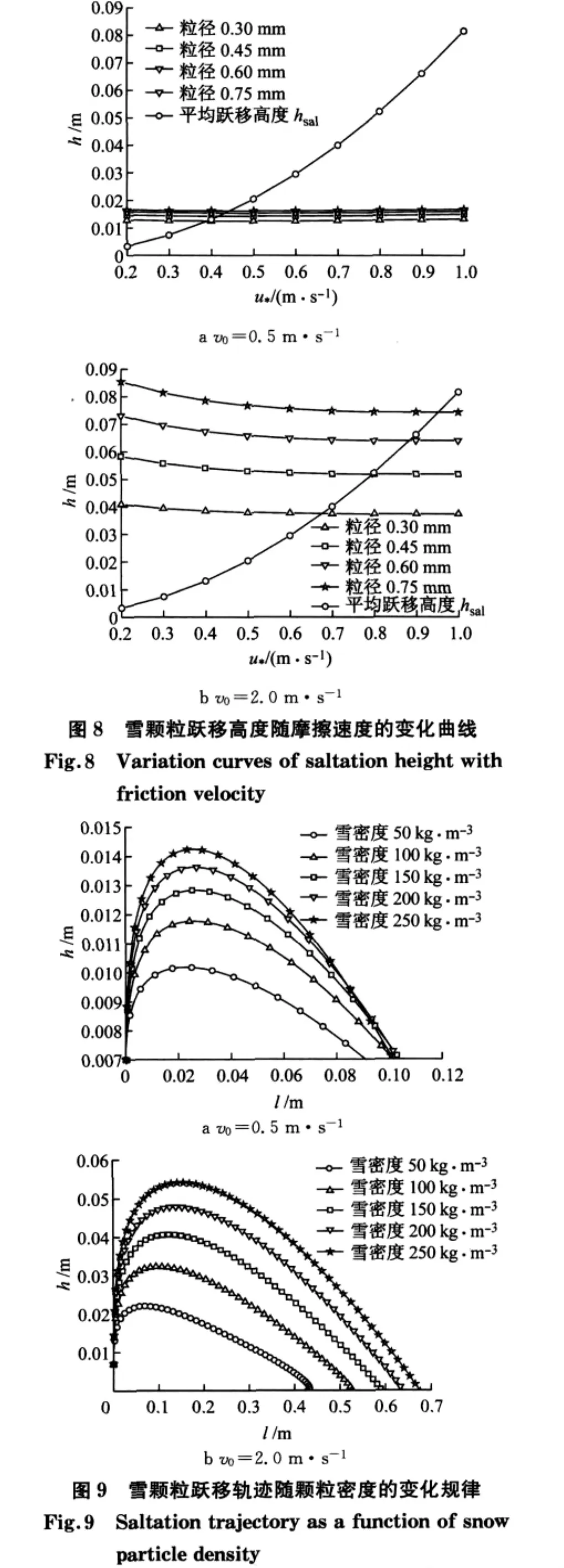
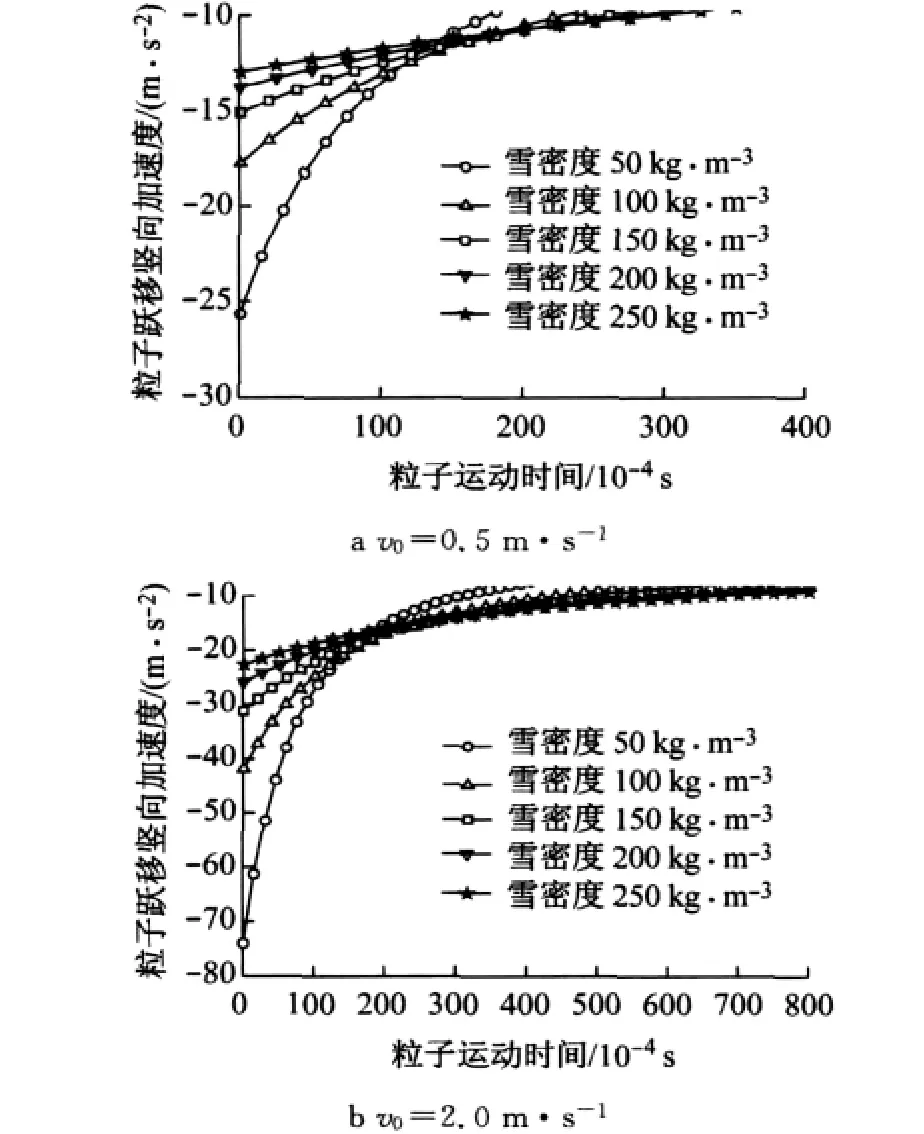
图10 雪颗粒竖向加速度随密度的变化曲线Fig.10 Variation curves of vertical acceleration with snow particle density
本文试图建立雪面侵蚀质量通量与粒子跃移数目之间的关系,假设单位时间单位面积上起跳的粒子数为s,mp为单个雪颗粒的质量,则mps为单位时间单位面积上起跳粒子的质量,物理意义上等价于壁面侵蚀量qero,表达形式见公式(4)与(5).即

下文的计算模型参考了文献[9](具体计算过程与之类似),记竖向初速度分布函数为f(v0),则单位时间、单位面积内从地面以初速度v0起跳的雪粒质量为

进一步可知,以初速度v0起跳的雪粒,在上升(↑)和下降(↓)阶段,高度y处的质量浓度表示为
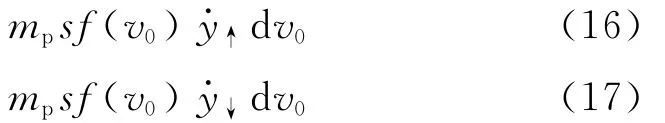
通过式(16)与(17),可以得到在高度y处单位时间内通过单位面积以初速度v0起跳的雪粒质量为
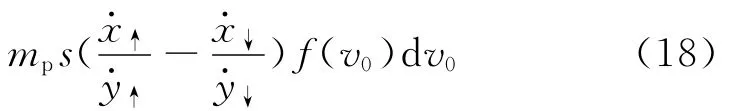
将式(18)对雪颗粒所有起跳的速度积分,并且从起跳位置高度至最大跃移高度处积分,便可得到以下颗粒跃移质量传输率的计算公式:
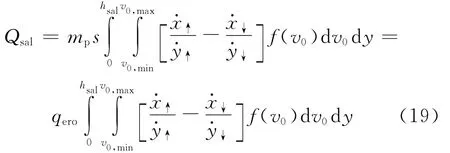
由公式(2)~(5)可知,qero有3种表达形式,即通过Iversen,Pomeroy和Beyers三者的经验公式变换,可分别记为qI,qP和qB,对应的跃移质量传输率记为QI,QP和QB.
4.2 与经验公式对比分析
将公式(19)与跃移质量传输率的经验公式(2),(3)进行对比,从而验证本文计算结果的合理性,具体见图11和图12给出的跃移质量传输率的变化规律.不难发现:
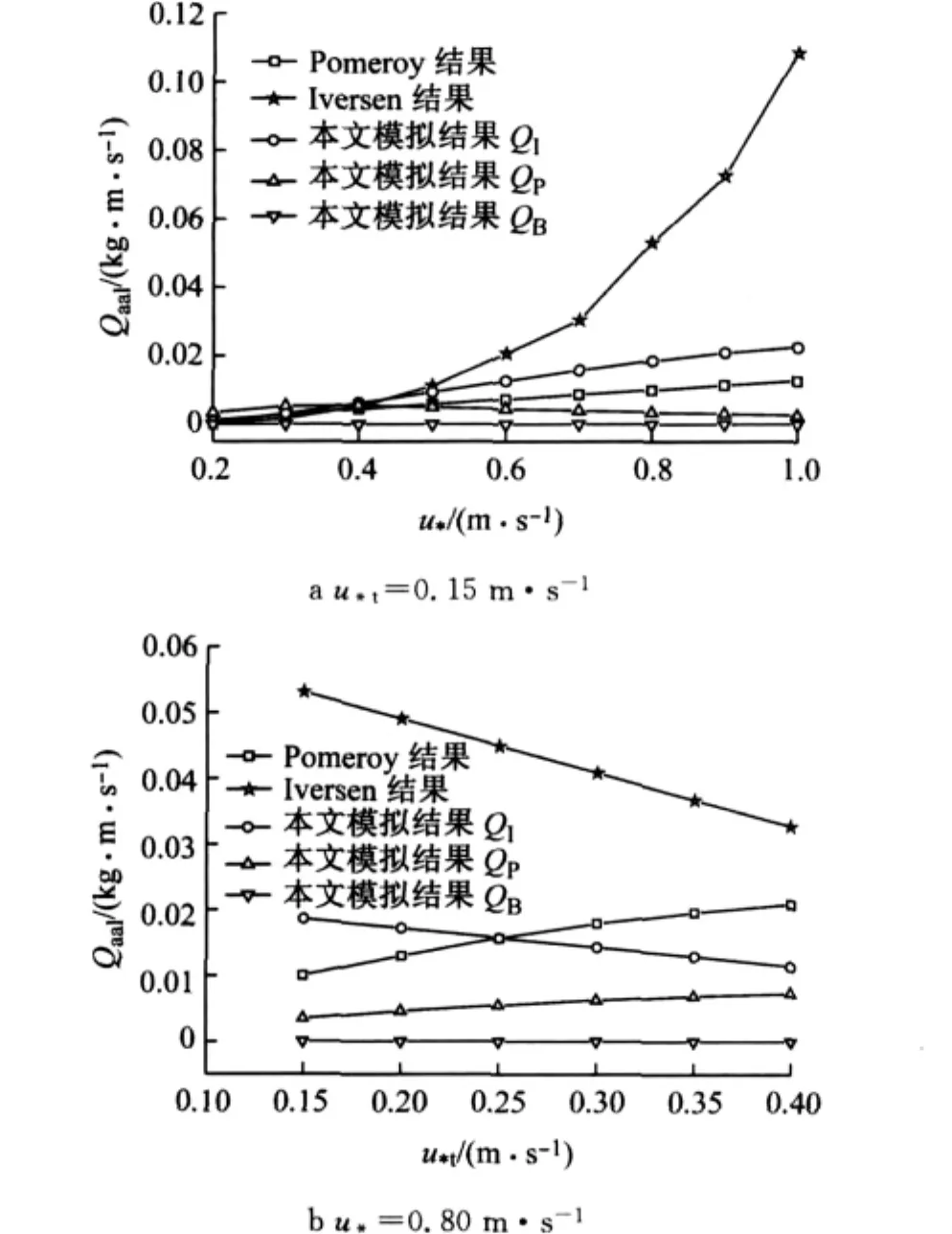
图11 雪颗粒跃移质量传输率随(阈值)摩擦速度变化规律(粒径0.30mm)Fig.11 Total snow mass flux as a function of friction velocity/threshold velocity(d=0.30mm)
(1)对比图11a和图12a,在摩擦速度较小时(如u*t<0.4m·s-1),本文的计算结果与经验公式吻合较好;在摩擦速度较大时,即粒子处于高风速情况下,Pomeroy与Iversen所计算出的结果相差很大,这是因为前者的计算结果与摩擦速度的平方成正比,而后者正比于摩擦速度的立方.此时计算结果QI的数值与经验公式最为接近.
(2)观察图11b和图12b,可知随着阈值摩擦速度的增大,Pomeroy公式计算的跃移雪质量传输率近似呈直线增加;Iversen公式的跃移雪质量传输率近似呈直线减小.Pomeroy与Iversen曲线趋势相反,因为后者与0.1m·s-1关系是负相关,故Iversen公式计算值减小;而前者与0.1m·s-1关系既有正相关,还有立方的负相关,总体呈现正相关(u*t<1.0m·s-1).可见,QI的数值基本介于两经验公式结果之间,趋势与Iversen曲线趋势相同.
(3)对比图11和图12,Pomeroy与Iversen所计算出的结果并未变化,因其是统计意义的平均值;但是本文的计算模型,随着粒径的增大,跃移雪质量传输率也随之增大.
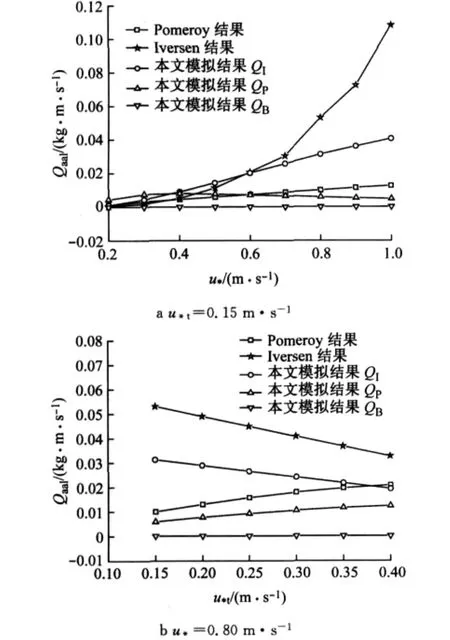
图12 雪颗粒跃移质量传输率随(阈值)摩擦速度变化规律(粒径0.45mm)Fig.12 Total snow mass flux as a function of friction velocity/threshold velocity(d=0.45mm)
5 结论
本文通过变化不同的颗粒运动参数,分析其与雪颗粒运动轨迹之间的变化规律.建立了雪面侵蚀质量通量与粒子跃移数目之间的关系,研究了粒子直径、摩擦速度等参数对质量传输率的影响,并与已有的经验公式比对分析,结论如下:
(1)随着雪颗粒直径、雪粒密度或者摩擦速度的增大,粒子的跃移高度也随之增大;粒子起跳速度不同时,水平跃移距离的变化规律也不同.
(2)本文提出的计算模型与空旷环境下的雪颗粒传输率经验公式计算结果基本吻合,证明了本文假定和方法的合理性,其中部分结果有待与实测或实验进行对比检验.
[1] Tominaga Y,Mochida A.CFD prediction of flowfield and snowdrift around a building complex in a snowy region[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,81(1/3):273.
[2] ZHU Zhiwen,LIU Zhenqing.CFD prediction of local scour hole around bridge piers[J].Journal of Central South University of Technology,2012,19:273.
[3] Uematsu T,Nakata T,Takeuchi K,et al.Three-dimensional numerical simulation of snowdrift[J].Cold Regions Science and Technology,1991,20:65.
[4] Naaim M,Naaim-Bouvet F,Martinez H.Numerical simulation of drifting snow:erosion and deposition models[J].Annals of Glaciology,1998,26:191.
[5] Gordon M,Taylor P A.Measurements of blowing snow,part I:particle shape,size distribution,velocity,and number flux at Churchill,Manitoba,Canada[J].Cold Regions Science and Technology,2009,55(1):63.
[6] Beyers J H M,Sundsb P A,Harms T M.Numerical simulation of three-dimensional,transient snow drifting around a cube[J].Journal of Wind Engineering and Industrial Aerodynamics,2004,92(9):725.
[7] Zhou X Y,Li X F.Simulation of snow drifting on roof surface of terminal building of an airport[J].Disaster Advances,2010,3(1):42.
[8] 周晅毅,李雪峰,顾明.风致积雪运动数值模拟的两方程模型方法[J].空气动力学学报,2012,30(5):640.
ZHOU Xuanyi,LI Xuefeng,GU Ming.Two-equation model for numerical simulation on snow drifting[J].Acta Aerodynamica Sinica,2012,30(5):640.
[9] 黄宁.沙粒带电及风沙电场对风沙跃移运动影响的研究[D].兰州:兰州大学土木工程与力学学院,2002.
HUANG Ning.Electrification in wind-blown sand flux and its influence to wind-blown sand saltation[D].Lanzhou:School of Civil Engineering and Mechanics of Lanzhou University,2002.
[10] Huang N,Sang J,Han K.A numerical simulation of the effects of snow particle shapes on blowing snow development[J].Journal of Geophysical Reserch,2011,116,D22206,doi:10.1029/2011JD016657.
[11] LüX H,Huang N,Tong D.Wind tunnel experiments on natural snow drift[J].Science China Technological Sciences,2012,55:927.
[12] Iversen J D. Drifting-snow similtude-transport-rate and roughness modeling[J].Journal of Glaciology,1980,26(94):393.
[13] Pomeroy J W,Gray D M.Saltation of snow[J].Water Resources Research,1990,36(7):1583.
[14] Carrier C F.On slow viscous flow[R].Providence:Brown University,1953.
[15] 李雪峰.风致建筑屋盖表面及其周边积雪分布研究[D].上海:同济大学土木工程学院,2011.
LI Xuefeng.Research on snowdrifting on building roof and around building.[D].Shanghai:College of Civil Engineering of Tongji University,2011.
[16] Anderson R S,Hallet B.Sediment transport by wind:toward a general model[J].Geological Society of America,1986,97:523.
[17] 朱光耀.公路风吹雪雪害形成机理与防治[M].哈尔滨:黑龙江人民出版社,2007.
ZHU Guangyao.The formation mechanism of Snowdrift disaster on highway and its control[M].Haerbin:Heilongjiang Publishing Group,2007.
[18] 李岁虹.稳态风沙运动的物理力学特性研究[D].兰州:兰州大学土木工程与力学学院,2005.
LI Suihong.Physical and mechanical characteristics of the steady state of sand movement[D].Lanzhou:School of Civil Engineering and Mechanics of Lanzhou University,2005.

