基于形态梯度变换和改进支持向量机的多普勒雷达天线机械故障诊断方法

甄树勇，蒋 涛，梁如意，王硕飞，靳 松

（1.河北省气象技术装备中心，河北 石家庄 050021；2.邯郸市气象局，河北 邯郸 056001）

前言

多普勒天气雷达具有高时空分辨率、及时准确的遥感探测能力，是中小尺度灾害性天气监测预警等方面极为有效的工具，从而在我国的相关气象部门获得了广泛的应用［1］。但是，由于雷达的构造十分复杂，一旦雷达出现故障，将使气象部门无法正常的检测气象信息，从而可能由于无法及时的预报而对人民的生命财产安全造成重大的损失。通过相关的分析发现，雷达的故障失效，很大一部分是由机械故障引起的，并且故障造成的危害最为严重，故障信号复杂多样，展现出较大的冲击，强噪，非线性等特点。为了能够对雷达的故障进行有效的诊断，有必要研究既能滤除背景噪声，又能对故障进行精确定位的故障诊断分类方法［2－5］。

目前对于噪声的消除和冲击信号的提取，应用较为广泛的有小波变换、EMD分解。但是小波信号存在母小波的选择问题，而EMD分解现在还没有明确的数学验证。因此在实际的应用中具有一定的局限性。数学形态滤波是一种新型的非线性滤波方法，能够将复杂的信号分解为各具物理意义的部分，并将其与背景分离，同时保持其主要的形态特征，已经在机械系统获得广泛应用［6－8］。但是，形态学滤波对于冲击信号不太敏感，而数学形态梯度作为检测冲击信号，消除噪声的一个重要方法，能够有效的提取冲击信息。本文通过形态梯度运算有效的实现故障信号的消噪和冲击的提取［9－10］。

为了实现故障的有效定位和分类，神经网络、支持向量机等较多优秀的故障识别方法被不断的发展与应用。但是神经网络过分强调克服学习错误而存在泛化能力不强，隐单元的数目难以确定，初值对网络的权值影响较大等问题，造成了神经网络在故障诊断方面的严重不足。支持向量机作为一种较新的学习分类方法，表现出了较强的分类能力和泛化性能［11］。为了实现多元故障的有效分类，采用一对余（one－versus－rest，OVR）的方法，通过组合多个两类分类器，构造多元支持向量机完成分类。一对余方法中各个SVM都是在全部训练样本上进行学习训练，当样本数较多时，训练速度较慢，效率也不高。有向无环图法在构造决策树的时候决策节点的选择具有随意性，容易产生累积误差［12］。

本文针对以上存在的问题，结合雷达故障信号的特点。提出基于数学形态梯度的信号检测和消噪方法，以及贝叶斯优化支持向量机的方法。通过滤波和诊断，对故障信号的特征进行了较为全面的展现，精确实现故障的定位。

1 数学形态梯度运算

数学形态学是在随机集和积分几何基础上发展起来的非线性分析方法，是一种非线性信号分析处理的工具，其主要特点是不存在相移和幅度的衰减等问题。数学形态变换对信号波形特征的研究完全在时域进行，与傅立叶变换和小波变换相比，计算简便，仅有加减和取极值运算，具有并行快速和易于实现的特点。形态变换包括腐蚀、膨胀、开运算、闭运算、击中、细化和粗化等7种基本运算，其中腐蚀、膨胀是两个基本运算，通过这两个基本运算，可以推导出其他的形态学变换。

设原始信号f（x）为定义在Df上的离散函数，定义结构元素g（x）是Dg上的离散函数，且Df和Dg分别为f（x）和g（x）的定义域，则f（x）关于g（x）的腐蚀和膨胀分别定义为：

式中：（x＋y），（x－y）∈Df，y∈Dg。

f（x）关于g（x）的开运算和闭运算分别定义为

这里符号Θ、8、·和·分别表示腐蚀、膨胀、开运算和闭运算。腐蚀和膨胀的计算形式和卷积相似，通过加减运算代替了相关乘积，开闭运算均具有低通特性，它们的组合可用做形态学滤波。

腐蚀和膨胀均可以视为有效的滤波器，为了提取信号的奇异性，采用如下的方式构造Grad（f）

在故障信号的处理过程中，形态梯度是显示故障脉冲的有力工具。可以有效的提取信号波形中的上升沿和下降沿。本文采用扁平结构元素，为了提取故障信号的突变，扁平结构元素应具有不同的起点，定义为：

其中：结构元素g＋和g－分别表示提取故障信号的上升、下降边沿，均值为0；l为结构元素的长度。gl和g1表示形态学运算的原始位置。主要是为了错开腐蚀和膨胀的操作，从而避免正负突变相互抵消。

根据膨胀、腐蚀、形状梯度的定义，可知提取故障的上升突变，有

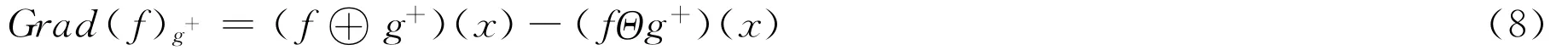
提取信号的下降突变，有

则总的检测故障突变的表达式如下：

形态梯度常用来在图像中进行边沿检测。如果某一点处的梯度值大，则表示在该点处图像的明暗变化迅速，从而可能有边沿通过。在一维信号处理中，形态梯度是凸显脉冲信息的有力工具，可以有效地检测出脉冲的位置，较好地保留脉冲的形状。基于形态梯度的上述特性，本文提出基于形态梯度提取隐含在振动信号中的反映雷达齿轮箱故障信息的脉冲特征。

2 多元分类器构造过程中的不足

支持向量机多元分类策略的基本思想：首先在多元分类方法中组合一对一模式的支持向量机，其次，构造分类器，当类别个数为n时构造n（n－1）／2个分类器，最后，利用投票法对样本点进行归属，得票最多的为类即为样本点所在类。

分类器优化可通过式（11）得到：

其中，i和j分别为第i类和第j类分类器。

其约束条件为：

作如下判断：

当故障较少时，上述分类思想在应用中较为精确，但是当故障较多或者较大时，有可能会出现某个样本在多个类中得票相同的情况，从而造成数据的不可分析。如图1所示。

图1 未知区域示意图

3 建立贝叶斯优化投票策略

贝叶斯分析描述了学习器对于数据特定假设

的似然性的先验函数。它的出发点是假设集合上的先验分布，为了使后验概率分布最接近于真实统计模型，最大化数据的后验概率密度。这样，对于不可分区域的数据，就可以有效的实现数据的分析和处理。本文采用贝叶斯概率统计进行投票策略优化，

设Pi表示x属于类Wi的概率，Pj表示x属于Wj的概率，Pi，j表示x既属于Wi又属于Wj，但是将其归入Wi的概率。则Pi的后验概率分布为［13－16］：

由（14）式可见，Pi，j与Pi近似成正比，有先验分布可得当Pi，j较大时，x属于Wi。

因此先验概率分布Pi，j函数应选增函数，因此选择先验分布函数为Beta（a，b）。函数介绍如下：

在这里R代表Pi，j。当0＜b≤1，a＞1时，Beta（a，b）为R的增函数。从贝叶斯估计的稳健性的角度来看，尾部越细的先验分布常使贝叶斯估计的稳健性越差。因此，a不宜过大，应有一个界限。设c为a的上限（c＞1，c为常数），即有1＜a＜c。

由此可见，a，b分别服从（1，c），（0，1］上的均匀分布。又因为当b＝1，1＜a＜c时Beta（a，b）＝Beta（a，1）＝aRa－1为R的增函数。

图2 未知区域正确区分后的示意图

取a＝2，得出先验概率估计，由（14）式可得相应的后验分布，根据后验分布对数据进行分类，从而提高支持向量机的诊断效果。

4 实际应用

本文的流程框图如图3所示，首先将采集到的振动信号进行形态学梯度滤波，从而有效的提取冲击、非线性特征，然后将滤波后的信号进行EMD分解，并求取特征分量的能量熵，从而获得最敏感的特征参数，将提取的特征参数输入到改进的支持向量机中进行模式的识别，从而实现故障的有效诊断。

本文通过多年来对某种多普勒雷达的齿轮箱重点部位进行实时监测，如齿轮箱轴承故障信号进行采集和分析，获得了该类雷达的轴承在发生内圈、外圈和滚动体故障时的振动数据，采集的设备部位如图4所示。

图3 本文的算法流程图

图4 某型号多普勒雷达齿轮箱整体显示图

获得的内圈的故障振动信号显示如图5所示。

对信号进行形态学梯度滤波（选择扁平型结构元素，尺度为10），滤波后的效果如图6所示。

为了证明形态学提取算法的有效性，将形态学梯度算法（选择扁平型结构元素，尺度为10），形态学滤波方法（选择扁平型结构元素，尺度为10），小波滤波（db5小波），EMD滤波的效果进行对比，结果如表1所示。

图5 某型号多普勒气象雷达轴承内圈振动信号图

图6 内圈信号去噪后的效果图

表1 几种滤波方法效果对比结果表

从表1可以看出，基于形态学梯度的滤波方法较传统的形态学滤波方法和基于EMD以及小波的滤波方法在去噪效果上更加明显，因此，验证了选用形态学梯度进行滤波的有效性。

对滤波之后的信号作如下处理：

Step1 选取滤波之后的训练样本。选择滚动体、内圈、外圈故障信号以及作为比对的正常信号各6组，以上四种信号的状态测试样本各选择3组。

Step2 初始化。期望初始化为1，2，3。并通过EMD分解数据，得到多个IMF分量。

Step3 计算在初始化中得到的各个IMF分量的能量，并利用能量熵值比较判断。振动信号经过EMD分解，能够得到n个IMF分量，每个IMF分量的能量分别为E1，E2，…En。

Step4 对特征因子进行单位向量化，由于故障较大时期对应的能量Ei数值较大，给数据分析带来不便，因此按以下步骤对特征因子进行单位向量化。

1）对信号进行分解，得到n个IMF分量；

2）分别求出每个IMF分量的能量Ei；

3）对n个IMF分量能量进行归一化处理；

4）计算能量熵。

将获得的能量熵作为支持向量机的输入，为了验证改进支持向量机算法的有效性，本文通过传统的支持向量机以及改进后的支持向量机的诊断效果进行对比，如图7所示为将熵值直接输入未经改进的支持向量机的结果，（本文选取RBF支持向量机）。

从图中可以看出，数据冗余聚集性较为严重，向量机识别效果并不明显，存在不可区分的区域，不能对故障进行有效地分类。

将熵值函数输入到改进投票策略的支持向量机，获得的分类结果如图8所示。

图7 未处理的向量机识别效果图

图8 处理后的支持向量机识别效果图

通过图8可以看出，通过改进后的支持向量机的分类效果明显增强，实现了雷达故障的准确判定。

5 结论

本文通过形态学梯度算法和支持向量机对某型号雷达的轴承故障信号进行了分析。首先通过形态学梯度较好的提取了故障信号的冲击信息，并抑制了噪声的干扰。然后，针对传统支持向量机中存在的不可分问题，提出了基于贝叶斯优化支持向量机的分类方法，利用Beta（a，b）优化了支持向量机分类器的投票方法。通过贝叶斯估计的先验概率统计，可以较好的估计出后验概率。从而实现对模糊区域数据的所属类别分析，提高了向量机对于不可分区域的识别准确率。为雷达的机械部分故障诊断提供了一种有效的识别方法。

［1］ 蒋小平.四川省多普勒天气雷达远程视频监控和故障会商系统的设计与实现［D］.成都.电子科技大学.

［2］ 马振贵，孙艳，郝智利.714C气象雷达收发系统故障的分析和排除［J］.山西气象.2003.4（65）：42－43.

［3］ 谭君.气象雷达常见故障分析［J］.中国民航学院学报.2004.22：24－25.

［4］ 王淑娟，汤峰昌，汤东.L波段雷达常见故障分析与处理［J］.现代农业科技.2010.4.312－314

［5］ 曲绍君.CINRAD／CC雷达运行保障技术研究与开发［D］.吉林大学.

［6］ 于湘涛，褚福磊，郝如江.基于柔性形态滤波和支持矢量机的滚动轴承故障诊断方法［J］.机械工程学报.2009，45（7）：75－80.

［7］ 胡爱军，王维珍，唐贵基，等.基于数学形态学的旋转机械振动信号处理方法［J］.噪声与振动控制.2005，6（3）：16－21.

［8］ 章立军，杨德斌，徐金梧，等.基于数学形态滤波的齿轮故障特征提取方法［J］.机械工程学报.2007，43（2）：71－75.

［9］ 卢官明，李妹虹.多尺度形态梯度算法及其在图像分割中的应用［J］.信号处理.2001，17（1）：37－40.

［10］ 郑涛，谷君，黄少锋，王增平.基于数学形态梯度的变压器转换性故障识别新判据［J］.中国电机工程学报2008，20（22）

［11］ 邓乃扬，田英杰.数据挖掘中的新方法—支持向量机［M］.北京：科学出版社，2004.

［12］ 吴德会.改进投票策略的多类SVM及在故障诊断中应用［J］.系统工程与电子技术，2009，4（31）：982－987

［13］ 王晓红.基于概率投票策略的多类支持向量机及应用［J］.计算机工程，2009，1，（35）：180－183

［14］ N Cristianini.J S Taylor.An Introduction to Support Vector Machines and Other Kernel－based Learning Methods.New York：Cambridge Univ－ersity Press，2000.

［15］ Smola A，Scholkopf B，MullerK R.The Connection between Regularization Operators and Support Vector Kernels［J］.Neural Networks，1998，11（4）：637－649.

［16］ Xu Xin，WangXuening.An adaptive network intrusion detection method based on PCA and support vector machines，Lecture Notes in Artificial intelligence 3584，2005：696－703.