Hamming方案H（n，3）上的相对2－设计的Fisher型下界

赵晓雪

（河北师范大学 数学与信息科学学院，河北 石家庄 050024）

结合方案上的相对t－设计是由P.Delsarte在1977年提出的［1］。近几年许多数学家对其进行了深入研究［2－5］。特别地，Bannai在文献［2］中给出了一般的Q－多项式结合方案的相对t－设计的等价概念和相对2e－设计的Fisher型下界：dim（L0（S）＋L1（S）＋…＋Le（S））。同时指出：清晰地给出Q－多项式结合方案的相对2e－设计的Fisher型下界，即确定L0（S）＋L1（S）＋…＋Le（S）维数的具体表达式是非常有意义的。本文给出了Hamming方案H（n，3）上的相对2－设计的Fisher型下界的清晰表达式。

1 预备知识

本节我们介绍Q－结合方案上的相对t－设计的概念和相关性质。关于结合方案的相关理论，详见文献［6］－［8］。设X＝ （X，｛Rr｝0≤r≤d）为类数为d的对称结合方案。固定X中的一个顶点u0。令Xr＝ ｛x∈X｜（u0，x）∈Rr｝（r＝0，1，…，d）.称｛Xr｝rd＝0为X的壳。设F（X）是X上所有实值函数构成的向量空间。显然F（X）可以看做X以标记的所有列向量构成的向量空间R［X］.以下设X具有关于本原幂等元序E0，E1，…，Ed的Q－多项式结构。对每个Ej，令Lj（X）为所有Ej的列向量张成的F（X）的子空间。则对于任意0≤j≤d，Lj（X）的维数等于Ej的秩等于重数mj.定义L（X）中任意两个函数f和g的内积则F（X）有正交直和分解：

设（Y，w）为X的带权子集。令｛ν1，ν2，…，νp｝＝ ｛r｜Xr∩Y≠ ∅｝。我们称（Y，w）由p个壳S支撑，其中S＝Xν1∪Xν2∪ … ∪Xνp.记Yνi＝Xνi∩Y，i＝1，2，…，p.

定义1 ［2，Definition 4.4］令（Y，w）为由p个壳S支撑的带有正权函数w的子集。称（Y，w）为关于u0的相对t－设计，如果对任意函数f∈L0（X）⊥L1（X）⊥…⊥Lt（X），下面条件

定理1 ［2，Theorem4.7］令（Y，w）为由p个壳S支撑的相对2e－设计。则下面不等式成立：

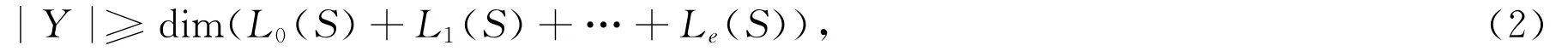
其中Lj（S）＝ ｛f｜s｜f∈Lj（X）｝，j＝0，1，…，e，S＝Xν1∪Xν2∪ … ∪Xνp.

定义2 ［3，Definition 1.3］如果定理1中的不等式等号成立，则（Y，w）称为一个关于u0紧相对2e－设计。

注1 ［3，Remark 1.4］猜想dim（L0（S）＋L1（S）＋…＋Le（S））＝me＋me－1＋…＋me－p＋1对于所有Q－多项式方案成立。文献［5］已证明对于Hamming方案H（n，2）猜想成立。

本文将证明猜想对于Hamming方案H（n，3）的相对2－设计也是成立的。

2 主要结论及其证明

首先Hamming方案H（n，3）是Q－多项式结合方案［6］。令F＝ ｛－1，0，1｝，X＝Fn是H（n，3）的顶点集。设x∈X和一个整数i（0≤i≤n），规定Γi（x）＝ ｛y∈X｜（x，y）∈Ri｝.以下考虑所有的相对设计均是关于固定顶点u0＝（0，…，0）的。设P为其第一特征值矩阵，Q为其第二特征值矩阵。则

本原幂等元Ej的秩。

下面定理是本文主要结果。

定理2 令（Y，w）是Hamming方案H（n，3）关于u0的由p个壳S支撑的相对2－设计。则有

其中S＝Xv1∪Xv2∪ … ∪Xvp，1≤v1，v2，…，vp≤n.

为证明定理2成立。我们首先定义一些函数和矩阵以及证明若干命题。

设u∈X和整数i（0≤i≤n），规定X到R上的实值函数

那么对任意x∈X，有记φ0＝设Y是X一个子集，有时也用来表示.设整数表示一个｜Xk｜×｜Xj｜的矩阵，对于任意z∈Xk，x∈Xj，有

命题1 （1）dim，（L0（Xk））＝Rank（M（0）k，0）＝1，（0≤k≤n）.

证明 （1）显然成立。下面我们证明（2）。首先由定义，dim（L1（Xk））＝Rank（Mk（1，1））成立。下面我们考虑m1×m1矩阵这里令（x，y）∈X1×X1.则

如果x＝y，那么

从而

如果（x，y）∈R1，那么

从而

如果（x，y）∈R2，那么

从而

其中

命题2 φ0是L1（Xk）的一组基；当时是L1（Xk）的一组基；当时，对于任意取定的是L1（Xk）的一组基.

证明 由命题1知，前两个结论成立。对于第三个结论，只需证明线性无关。我们不妨假设u＊＝u2n，令

对于任意给定的ui（1≤i≤2n－1），选取x，y∈Xk，使得

并且ui∈Γk－1（x），ui∉Γk－1（y）成立。设V＝Γk－1（x）∩Γk－1（y）.那么故从而4Ci＝0.由i的任意性线性无关。

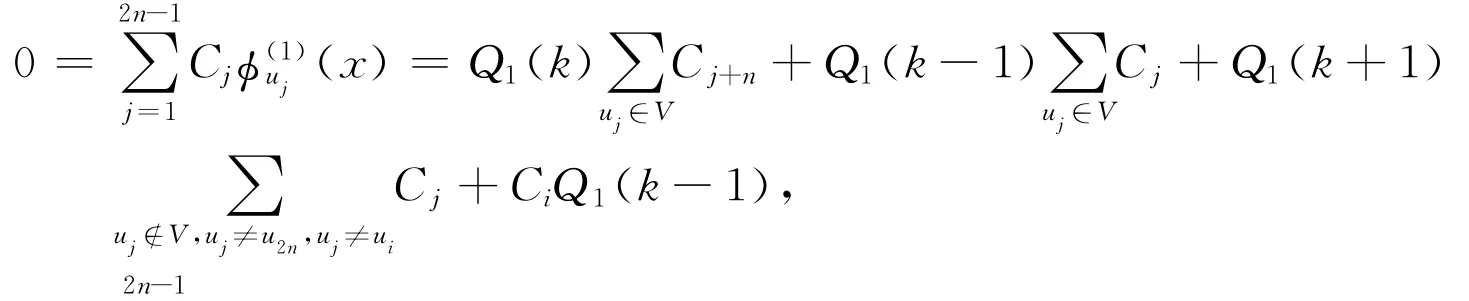
命题3 dim（L0（Xk）＋L1（Xk））＝2n，其中1≤k≤n.

选取ui，uj∈X1，使得故

从而φ0∈L1（Xk），因此L0（Xk）⊂L1（Xk）.所以dim（L0（Xk）＋L1（Xk））＝dim（L1（Xk））＝2n.

设

选取适当的x，y∈Xk，使得

并且ui∈Γk－1（x），ui∉Γk－1（y）；u2∈Γk－1（y），u2∉Γk－1（x），成立.设V＝Γk－1（x）∩Γk－1（y）.则

从而CiQ1（k－1）－CiQ1（k＋1）＝0，推出4Ci＝0.因此，对任意1≤i≤2n且i≠2，我们有Ci＝0.从而有C0φ0C0＝0，所以dim（L0（Xk）＋L1（Xk））≤dim（L0（Xk））＋dim（L1（Xk））＝1＋ （2n－1）＝2n，我们得到是线性无关的。又因为2n≤dim（L0（Xk）＋L1（Xk））＝2n.并且是L0（Xk）＋L1（Xk）的一组基.

命题4 如果p≥2，则有（1）dim（L0（S））＝1；（2）dim（L1（S））＝2n.这里S＝Xν1∪Xν2∪ … ∪Xνp，1≤ν1，ν2，…，νp≤n.

证明 （1）是显然的.下面我们来证明（2）.对于任意ui∈X1，有φu（1i）∈L1（S）.设

因此p≥2，所以存在一个且Xk⊂S.取x∈Xk，有成立.根据命题1，有，因此对任意ui∈X1，都有Ci＝0.得到2n＝dim（L1（Xk））≤dim（L1（S））≤2n，所以dim（L1（S））＝2n.

命题5 如果p≥2，则有dim（L0（S）＋L1（S））＝1＋2n，且是L0（S）＋L1（S）的一组基，这里S＝Xν1∪Xν2∪ … ∪Xνp，1≤ν1，ν2，…，νp≤n.

证明 当p＝2时，设S＝Xk∪Xl.根据命题4，我们有是L1（S）的一组基.接下来，我们证明｛φ0｝和是线性无关的.设

分别在等式（12）两边取x∈Xk，y∈Xl的值之和，我们得到下面的两个等式：

等式（13），（14）是以C0和为未定元的方程组，系数行列式为：

因为k≠l，上面行列式不等于零.因此.因为｝是L1（S）的一组基，所以对于任意ui∈X1，我们有Ci＝0.于是dim（L0（Xk∪Xl）＋L1（Xk∪Xl））＝2n＋1，并且是L0（Xk∪Xl）＋L1（Xk∪Xl）的一组基.

当p＞2时

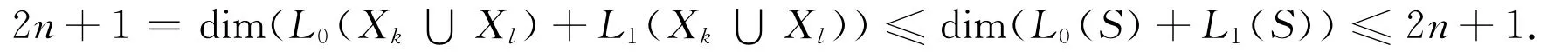
命题得证.

定理2的证明：当p＝1时，由命题3可证；当p≥2时，由命题5可证.

［1］ Delsarte，P.，Pairs of vectors in the space of an association scheme［J］.Philips Res.Repts，32（1977）：373－411.

［2］ Bannai，Ei.and Bannai，Et.，Remarks on the concepts oft－designs［J］.J.Appl.Math.Comput.，2012，doi：10.699 1007／s12190－012－0544－1.

［3］ Bannai，Ei.，Bannai，Et.and Bannai，Hi.，On the existence of tight relative 2－designs on binary Hamming association schemes，arXiv：.

［4］ Li，Z.T.，Bannai，Ei.and Bannai，Et.，Tight Relative 2－and 4－Designs on Binary Hamming Associ ation Schemes，Graghs and Combinatorics，（on line）DOI 10.1007／s00373－012－1252－1.

［5］ Xiang，Z.Q.，A Fisher type inequality for weighted－wise balanced designs，Journal of Combina torial Theory A，2012，119：1523－1527.

［6］ Bannai，Ei.and Ito，T.，Algebraic Combinatorics I：Association Schemes，Benjamin／Cummings，London，1984.

［7］ Brouwer，A.E.，Cohen，A.M.and Neumaier，A.，Distance－Regular Graphs，Springer－Verlag，Berlin，1989.

［8］ Godsil，C.D.，Algebraic Combinatorics［M］.Chapman and Hall，New York，1993.