采摘机械臂的滑模PID控制
宋文龙,杨 鑫,贾鹤鸣
(东北林业大学机电工程学院,黑龙江省哈尔滨市150040)
在中国,棉花种植地域辽阔,生产规模呈现多元化格局,具有品种多、纤维短、收获期长、以人工采摘为主等特点;常规人工手采棉质量稳定,市场欢迎,但由于拾花期短,劳动强度大,受拾花工不足的制约[1],每年采棉季节,需要雇佣数十万劳动力抢收棉花,仅人工费用就高达8亿元,且往往因劳动力不足延长了采棉期,影响了棉花的质量,妨碍了秋耕灌溉和来年的春耕生产[2];因此,适时收获和低成本收获是增加收入的有效方法。目前,美国棉花生产具有生产规模大、品种单一、纤维长、成熟期集中等特点,其机械化机械采收技术已是世界公认的成熟先进技术。采摘机器人机械臂的运动控制精度的提高是实现上述目标的有效合理的方法。
采摘机械臂的模型中一般包含非线性不确定项和未知的外界环境干扰,从而使上述控制问题变得难于实现,针对这一问题国内有许多学者提出了相应的解决方法[3-6],。机械臂模型存在外界的干扰和控制误差等问题,文献[7]提出一种模糊变结构控制方法来解决这个问题,但是模糊变结构控制需要模糊逻辑的建模,而模糊逻辑建模主要取决于经验且计算十分复杂不易于实现。也有一些采用后推法设计控制器的,例如文献 [8]和 [9]所提到的,但是由于后推法需要知道精确的机械臂数学模型,设计的控制器形式会过于复杂,设计控制器的难度大大增加。
本文针对采摘机械臂终端的精确跟踪问题,设计了一种具有自适应调节PID增益功能的滑模控制器,并且设计了饱和函数来抑制滑模控制器的高频抖振,仿真结果表明设计的控制器具有较高的精度,能够使得采摘机械臂精确的跟踪期望位置,具有较好的鲁棒性。
1 采摘机械臂模型
采摘机械臂动力学的模型一般可表示为:[10-14]
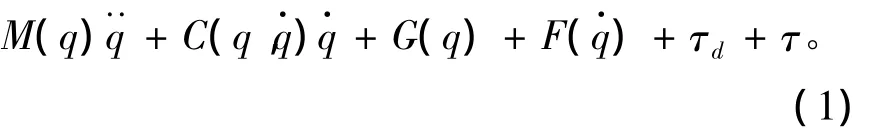
式中:q∈Rn表示关节的角位移,M(q)∈Rn×n表示机械臂的质量惯性矩阵,C(q,)∈Rn表示科氏力和离心力矩阵,G(q)表示重力矩阵,F()∈Rn表示摩擦力矩,τd∈Rn为未知的外界环境干扰,τ∈Rn表示机械臂的控制力矩。
选择如下的坐标转换,

式中:ξ1和 ξ2是系统的可测状态,则系统(2)可以表示为:
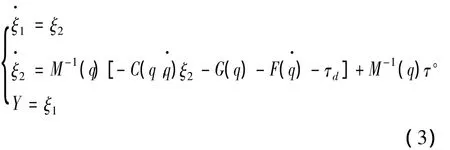
由于系统模型 (3)中包含模型不确定部分和未知的外界干扰,为了获得更简化的模型以便于控制器的设计,重新定义系统为:

式中:u是控制输入;Y为输出;b为控制增益;f(ξ1,ξ2)是模型的标称参量;Δf(ξ1,ξ2)是模型的不确定量;d表示外界干扰。假设存在2个正的上界g和α,且满足|Δf(·)|≤g和|d|≤α。定义e为机械臂的期望轨迹和实际输出轨迹Y之间的误差,并且满足e=Yd-Y。
2 采摘机械臂的滑模PID控制器设计
对于公式 (4)的第2个方程,为了使得系统稳定,定义如下误差系统:

式中:k1与k0为控制器的设计参数,仅需满足s2+k1s+k0=0的根在左半复平面上即可使得系统稳定。通常情况下可以设计参数满足k1=2ζωn且k0=ω2n;其中ζ表示阻尼比;ωn表示固有频率。
本节中提出的采摘机械臂的自适应滑模控制器设计过程可以分为2个步骤来实现。首先需要定义一个滑模面函数,其次是设计合适的控制律令该系统到达并保持在期望的滑模面σ=0上。
定义滑模面函数为

若期望的滑模面存在,则可以使得σ=0,令

将公式 (7)代入公式 (5)得:
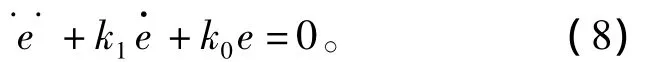
公式 (8)表示随着时间的增长 (t→∞),系统的跟踪误差最终会收敛至0(e→0)。
设计系统的控制输入u为,

其中,

增益k2表示一个正的标量参数,sgn(σ)为符号函数,满足

传统的PID控制器增益一般都是固定的,无法适应变化工况的控制品质要求,本文设计的3个控制增益kP,kI和kD可由如下的自适应律在线学习获得,其中ηi>0表示自适应的学习率,其中i=1,2,3。
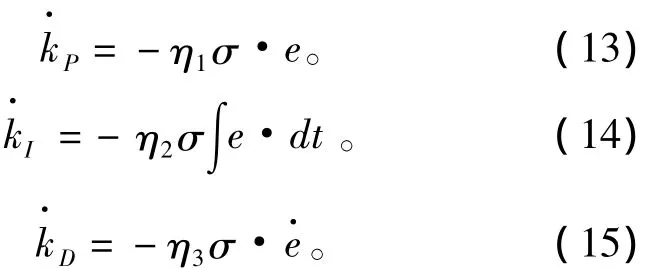
3 稳定性分析
为了证明上述设计的控制器的稳定性,选择Lyapunov函数如下:

对式 (16)求导可得,
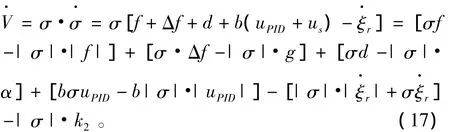
整理得
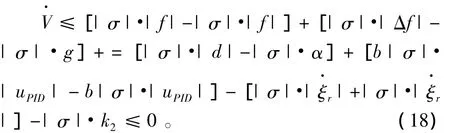
因此,通过本文设计的控制律 (9) ~(12),利用自适应学习律 (13)~(15)可以确保采摘机械臂的误差跟踪系统达到并保持在期望滑模面上,使得闭环系统渐近稳定。
由于滑模控制会产生抖振问题,使得实际系统的控制输入出现高频振动,容易损坏系统的执行机构,所以本文选择设计饱和函数来代替公式 (11)中的符号函数sgn(σ)来抑制控制器的抖振问题,选择的饱和函数如下:
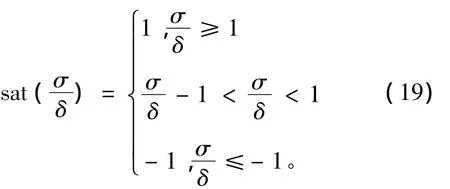
其中δ表示边界层宽度,通过如下设计后给定任意的初始值设计的滑模面函数σ都可以到达并保持在边界层|σ|≤δ内。
4 仿真分析
为了进一步验证所提出的控制器的有效性,针对采摘机械臂的模型,机械臂的期望跟踪路径设定为:1.0+0.2 cos(πt)和1.0+0.2 sin(πt). 在MATLAB软件环境下进行仿真,所选择的控制参数如下:选择阻尼比ζ=1.5,固有频率ωn=4,使s2+k1s+k0=0的根k1=12和k0=36在左半复平面的开区间上。PID控制器的增益kP,kI和kD初始值为0。学习率ηi设定为5,i=1,2,3。边界层设置为δ=0.2。根据设计的控制律 (10)~ (11),采摘机械臂的跟踪控制曲线如图1和2所示。
从图1和图2可以清楚地看出:采摘机械臂的位置和速度信息都能够快速的收敛到期望状态信息,即本文所提出的自适应滑模PID控制器在机械臂的轨迹跟踪的精确性上更有效,更优越。
5 结论
随着棉花生产农场化经营模式的推广和开放式、可变结构采摘机器人成本的降低,相信采摘机器人将在21世纪越来越多地应用于棉花生产中,大幅度提高优质棉的产量和农业智能化水平,最终实现棉花生产由粗放型经济向集约型经济的转变。
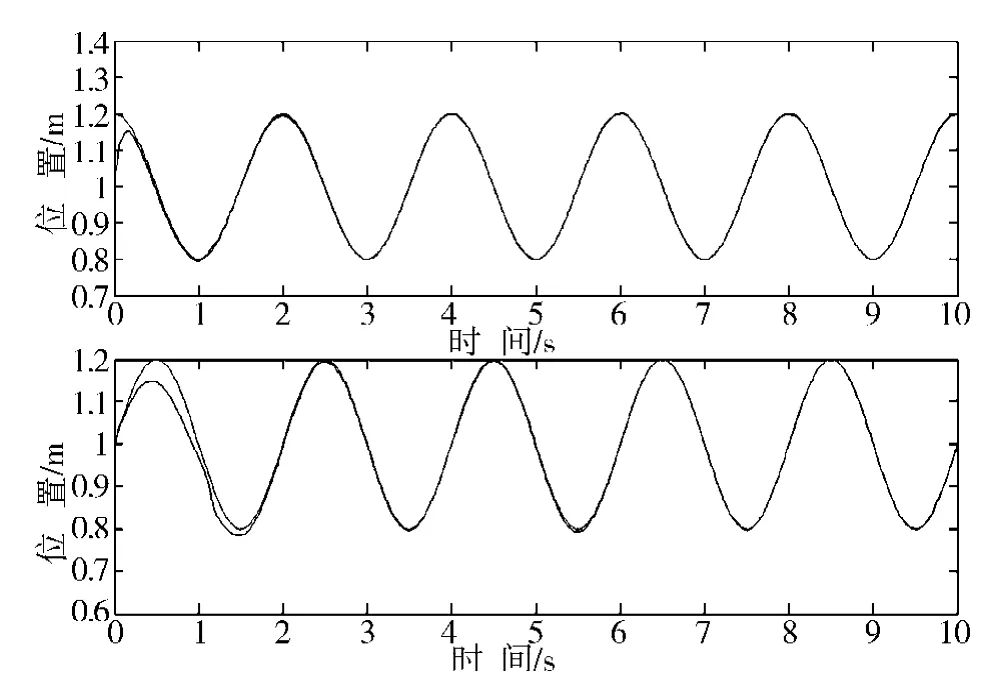
图1 采摘机械臂关节终端的位置跟踪Fig.1 Position tracking of terminal joint for manipulators

图2 采摘机械臂终端的速度跟踪Fig.2 Velocity tracking of terminal joint for manipulators
(1)针对采摘机械臂的轨迹跟踪控制问题,基于Lyapunov稳定性理论设计了一个具有PID增益自适应调节功能的滑模控制器。控制器的设计无需针对系统的线性化模型且不需要进行先验学习,它可以在线实时应用。
(2)设计的控制器具有满意的循迹跟踪效果,可以满足实际工程的应用需求。
[1]王 玲,姬长英.农业机器人采摘棉花的前景展望与技术分析[J].棉花学报,2006,18(2):124 -128.
[2]陈欣成.农垦农机化工作与农机更新换代的一些思路[J].农村机械化,1998(3):21-22.
[3]冯青春,纪 超,张俊雄,等.黄瓜采摘机械臂结构优化与运动分析[J].农业机械学报,2010,41(S1):244 -248.
[4]李 伟,李 吉,张俊雄,等.苹果采摘机器人机械臂优化设计及仿真[J].北京工业大学学报,2009,35(6):721 -726.
[5]唐志国,李元春,姜日花.机械臂协调操作柔性负载自适应模糊滑模控制[J].吉林大学学报(工学版),2011,41(2):484 -490.
[6]陈 辛.机械臂的动力学研究[D],哈尔滨:哈尔滨工程大学,2007.
[7] Jagannathan S,Lewis F L,Liu K.Motion control and obstacle avoidance of mobile robot with an onboard manipulator[J].Journal of Intelligent Manufacturing Systems,1994,5(5):287 -302.
[8]晁红敏,胡跃明,徐建闽.基于滑模和后推法的自适应轨迹跟踪[A].第20届中国控制会议论文集[C].大连:大连理工大学出版社,2001.
[9]林 雷,王洪瑞,任华彬.基于模糊变结构的机械臂控制[J].控制理论与应用,2007,24(4):643 -650.
[10]贾鹤鸣,宋文龙,郭 婧.基于神经网络滑模的采摘机械臂控制设计[J],吉林大学学报(工学版),2012,42(3):709 -913.
[11]王丽丽,郭艳玲,王 迪,等.果蔬采摘机器人研究综述[J].林业机械与木工设备,2009,37(1):10-11+14.
[12]王 迪,关晓平,郭艳玲.基于ARM的浆果采摘机械手运动控制研究[J].林业机械与木工设备,2009,37(4):22 -24.
[13]李俄锋,徐学林.基于Pro/E和ADAMS的林木干果采摘臂的运动仿真分析[J].林业机械与木工设备,2010,38(2):34 -36+48.
[14] Wai R J.Tracking control based on neural network strategy for robot manipulator[J].Neurocomputing,2003,51(10):425 - 445.

