环形激光陀螺零偏热效应补偿模型的研究*

周 璐，任 磊，刘晴晴，杜建邦

(宇航智能控制技术国家级重点实验室，北京100854)

激光陀螺具有结构简单、精度高、稳定性好、启动快、动态范围大和数字输出等诸多优点，目前已广泛应用于军用、民用的高精度捷联惯导系统之中。作为捷联惯性系统的核心器件，激光陀螺的精度除了受到制造工艺、内部结构等本身的性能影响以外，还与测试其精度时所处的环境条件和工作条件有关。

补偿技术旨在通过测量适当的误差系数，并利用这些值对测量值加以修正，以除去惯性敏感器中可预测的误差项。这些通常在系统软件中实现。除了敏感器误差补偿外，通常对各种系统误差也要进行补偿，如敏感器安装误差等。这些误差可以量测，因此它们对导航系统性能的影响是可以预测的。而测量的系数随时间、温度、振动、施加的运动以及逐次工作而变化，而正是这些变化最终决定了导航系统的性能。当不可能对大多数的这些误差加以补偿时，温度补偿常常是获得给定的性能目标的主要因素[1]。

由于温度变化影响的因素太多，很难通过理论定量的分析温度对某个因素有多大的影响及如何影响，但可以通过试验的方法来研究温度与陀螺零偏的关系，减小和补偿热效应对激光陀螺零偏的影响，最后建立激光陀螺误差热补偿模型并储存在导航计算机中，由软件进行实时补偿，这也是目前研究的热点。

传统的激光陀螺温度补偿方法侧重于对于误差模型中某一个具体因子的研究，对温度的建模通常是在陀螺内部某个静态温度点上考查较大范围内升、降温过程中温度冲击对陀螺性能的影响，设计动、静态温度建模结合的方法来对模型参数加以有效辨识[2]。本文研究的激光陀螺零偏热效应补偿模型，不局限于分析陀螺内部温度与零偏的关系，而是综合考虑陀螺自身温度变化与环境温度变化对陀螺性能带来的综合影响，这样的补偿模型也更加具有实际工程应用的意义。

1 环形激光陀螺的零偏误差模型

环形激光陀螺的误差类型主要有:温度、压力、磁场、闭锁现象、零位漂移、标度因素的变化、轴失准误差;而误差模型由零偏、标度因素、轴失准误差组成。其中，零偏误差模型公式如下[3]:

其中，Bf为安装零偏;Bt为温度零偏系数;ΔT为实际温度与参考温度差;B▽t为温度梯度零偏系数;▽T为温度梯度值;Bdi为电流零偏系数;DI为电流变化值;Bm为磁场影响零偏系数;M为磁场强度;Ba为加速度影响零偏系数;A为沿敏感轴加速度值;为随机零偏。

热效应对激光陀螺零偏的影响非常明显且难以精确建模。由于激光陀螺材料本身对温度的敏感性和周围温度场对激光陀螺工作状态的影响[4]，通常对于非常精确的惯性系统，要极为严格的控制其敏感器的温度。分析热效应对激光陀螺零偏的影响主要是分析3个方面，即温度变化、温度梯度与温变速率[5]。对应式(1)中的第2、3 两项。

2 热效应对环形激光陀螺零偏影响的机理

环形激光陀螺的零偏误差处理主要由热效应补偿来实现。热效应对环形激光陀螺的影响是一个综合过程，它不仅影响到环形激光陀螺内的氦、氖气体，还将影响到陀螺内部的所有结构件，需要考虑几何形变、物理参数和气体流场等所有因素。从热源来说，陀螺工作时自身要发热，需要一段时间才能达到平衡，而且在外部环境温度等条件发生变化时，温度场将变得更为复杂，也更难平衡，所以陀螺自身温度变化与环境温度变化都将影响陀螺的性能[6]。从几何特征来说，器件的热胀冷缩、弯曲变形都可造成光路变化，谐振系统损耗增加。从物理特性来说，材料的导热系数、气体的折射率、光学器件的光学性质也会变化。最后陀螺自身和外界温度场的变化引起气流流场的变化，使两臂的放电电流出现不平衡，加剧了朗谬尔流效应带来的零偏影响。这些变化都将影响激光陀螺的输出[7]。

3 环形激光陀螺的零偏漂移补偿

3．1 环形激光陀螺的温循试验

环形激光陀螺的性能随其壳体内温度改变造成的变化，可以通过将转台封闭在环境箱内来加以观测，如图1所示。数据采集系统由速率转台、工控PC机、I/O模块、转台控制模块、GPIB总线、高低温箱组成[8]。温循试验采用多种方式，主要有允许陀螺温度稳定的“吸收”试验和允许在给定周期内进行有控制的增加或降低的热梯度试验。上述试验在各种温度条件下重复进行并记录陀螺的输出信号，使其零偏值在陀螺工作范围内的各种温度条件下进行评估。

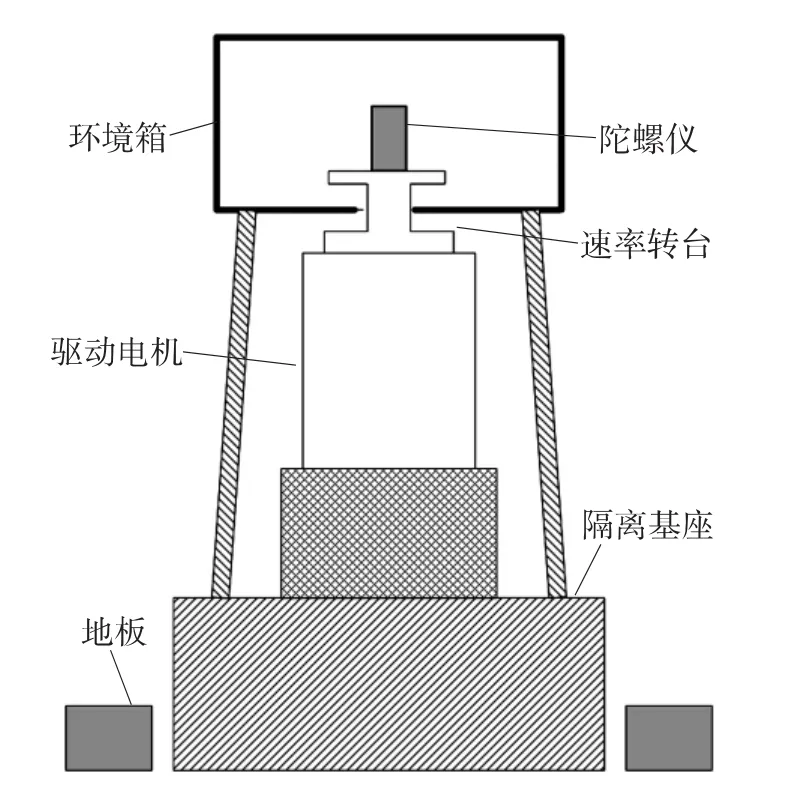
图1 温循试验设备示意图

为了验证环形激光陀螺的热效应特性，进行温循试验如下:将环形激光陀螺安装于转台的某一位置锁定，调整温箱值，将温度在13 h内先降低到－40℃再升高到70℃再恢复到初始温度。温箱内设置有温度传感器，外部面板显示温箱内的实时环境温度，当温箱内的实际温度达到－40℃时开始记录，每1 s计一个数，直到温箱内的温度达到70℃。为了减小量化误差，取每600 s数据的平均值作为参考数据。记录的结果如图2所示:图2(a)显示了零偏和时间的关系，图2(b)显示了零偏和温度的关系。

由图2(a)、(b)可以看出，环形激光陀螺的零偏随着温度的变化而变化，且有明显的迟滞效应，即陀螺响应的滞后。

3．2 零偏补偿模型

由于标定因数误差和轴失准误差引起的零偏非常小，可以忽略不计，所以陀螺的零偏输出如下:

其中，Ωoutput为陀螺的输出;Ωearthrate为地球自转速率。

零偏补偿模型理论公式如下[9]:

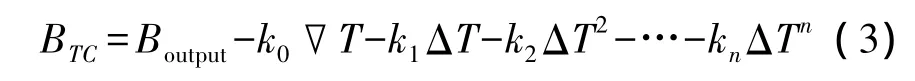
图2

其中，BTC为热效应补偿输出;Boutput为由于热效应引起的零偏;▽T为陀螺里的温度梯度;k0为温度梯度零偏系数;ΔT为实际温度与参考温度之差;k1～kn为温差零偏系数。

分析根据上述试验方法所记录的数据，在不考虑温度变化对环形激光陀螺影响的情况下，即不考虑式(3)中的第二项，可以得出环形激光陀螺在不同温差ΔT下的特性，求出温差零偏系数k1～kn。在环形激光陀螺的工程应用中，通常取ΔT的1阶或2阶。

在进行上述的零偏补偿后，温差值的影响初步消除了，但迟滞效应的影响还在。零偏迟滞与温变速率(ΔT/dt)有关，如下图3所示，在三个不同的温变速率0℃/h、10℃/h、20℃/h下，陀螺有不同零偏迟滞输出。可以看出，温变速率越快，迟滞效应越明显。

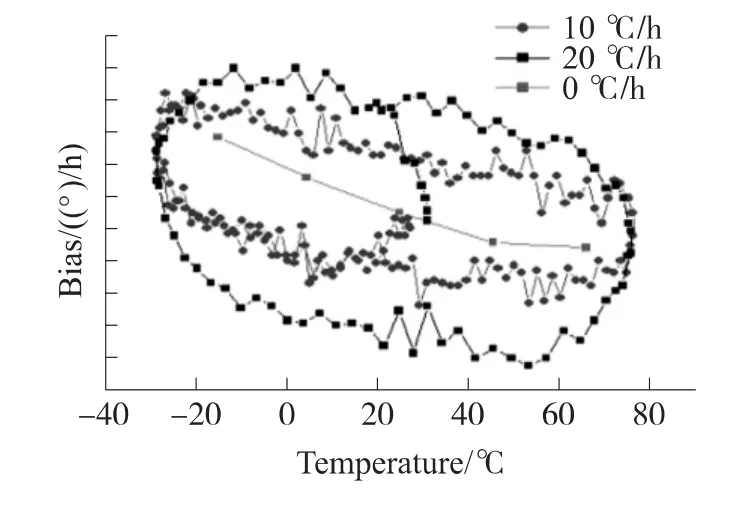
图3 不同温变速率下温度和零偏

由图2、3可以看出，环形激光陀螺的零偏可由温变速率ΔT/dt和与参考温度的温差ΔT来建模。而温变速率与陀螺内部的温度梯度有关，不同的温变速率造成了陀螺内部的不同温度梯度值，而不同的温度梯度使得陀螺内的结构件产生不同的热膨胀系数，进而导致迟滞现象，所以可以用温度梯度▽T代替温变速率ΔT/dt对零偏迟滞进行补偿。

研究补偿温差ΔT后的环形激光陀螺零偏迟滞与温度梯度▽T的关系，如图4所示。可以看出，零偏迟滞与温度梯度▽T基本成线性关系。因此，在工程实际应用中，可以近似用以下一阶线性数学模型对零偏和零偏迟滞进行补偿:

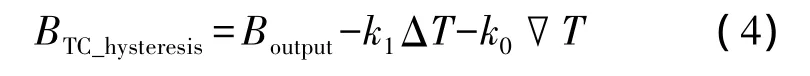
根据上述试验方法，用多元线性回归法或最小二乘法处理试验得出的数据，求出上式中的k0和k1，从而建立在某个参考温度点下，环形激光陀螺零偏与温差ΔT、温度梯度▽T之间的关系。在工程使用中，需要对每个环形激光陀螺进行高低温环境试验，通过相关的数学方法，根据式(4)建立零偏热效应补偿模型。

图4 零偏迟滞与温度梯度

如图5(a)可以看到在整个工作温度变化范围内，对环形激光陀螺进行补偿前后的零偏。蓝色点表示仅用温差ΔT进行补偿后的零偏，粉红色点表示用温差ΔT和温度梯度▽T进行补偿后的零偏。可以看出，补偿后的零偏值几乎不随温度变化而变化，基本消除了零偏随温度变化的趋势。

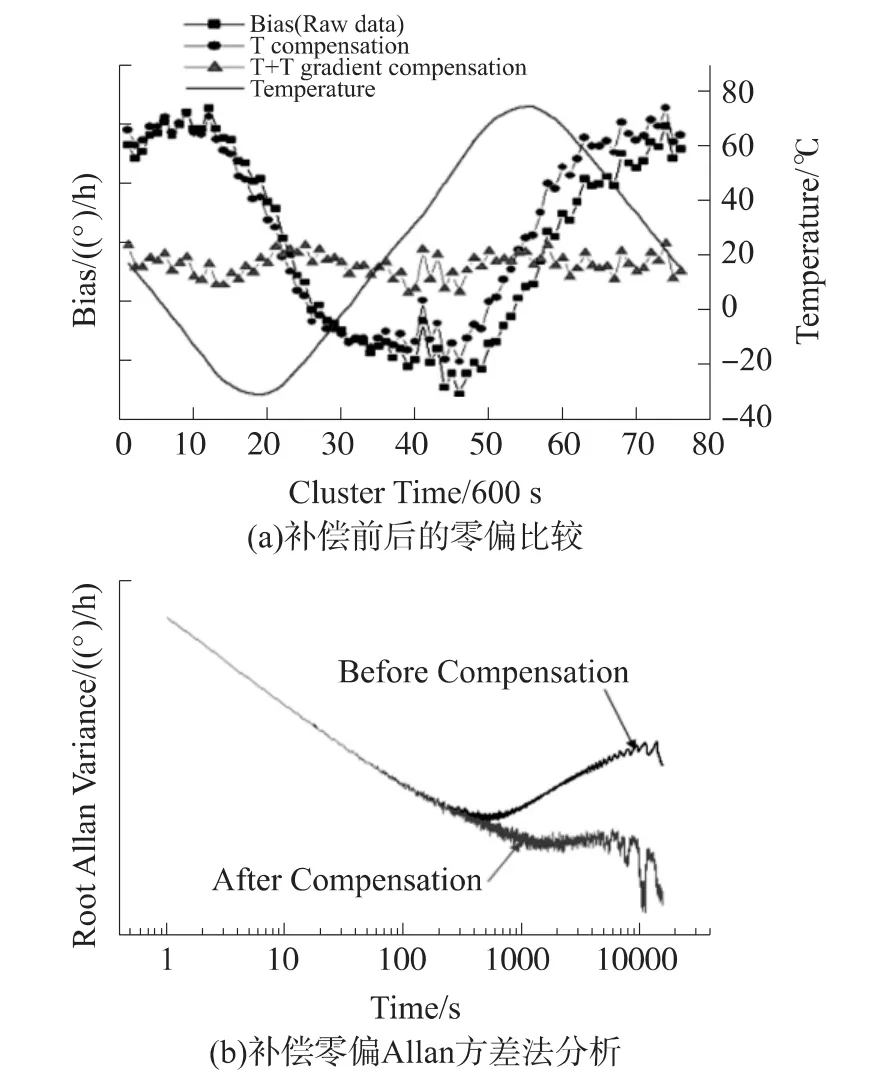
图5 补偿前后的零偏比较和补偿零偏Allan方差法分析

采用IEEE推荐的随机误差建模方法Allen方差分析法[10]对补偿前后的数据进行分析比较，由图5(b)可以看出补偿后的效果较好，计算得出零偏值的标准方差仅仅为为补偿前的0．13倍。

4 结论

本文提出了一种工程适用的环形激光陀螺的零偏热效应补偿模型，通过研究环形激光陀螺在工作的全温度范围内的零偏和温度变化、与参考值温差、温度梯度的关系，对环形激光陀螺的零偏进行热补偿，基本消除了零偏随温度变化的趋势，使零偏随温度几乎按水平直线的规律变化。补偿后陀螺的零偏漂移稳定性提高了87%，有效的减少了热效应对激光陀螺的影响，提高了激光陀螺的精度，具有重要的工程实际价值。

[1]David H Titterton，John L Weston．Strapdown Inertial Navigation Technology[M]．2nd Ed．USA:American Institute of Aeronautics and Astronautics，Inc．，2004:172－173．

[2]王淑娟，吴广玉．惯性器件温度误差补偿综述[J]．中国惯性技术学报，1998，6(3):44－49．

[3]Aronowitz F．Fundamentals of the Ring Laser Gyro[C]//Optical Gyros and Their Application，RTO AGARDograph 339，1999．

[4]闫钧宣，张科．激光陀螺温度误差补偿方法研究[J]．计算机测量与控制，2011，19(6):1452－1454．

[5]IEEE STD 647—2006，IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros[S]．

[6]张鹏飞，龙兴武，汤建勋，等．机抖激光陀螺的零偏的实时温度补偿方法研究[J]．传感技术学报，2007，20(6):1279－1282．

[7]吴国勇，顾启泰．温度对四频激光陀螺零偏的影响[J]．光学技术，2002，5(3):198－200．

[8]邓春林，周凤岐，蔡伟，等．RLG环形激光陀螺测试技术的研究与设计[J]．传感技术学报，2010，23(10):1435－1438．

[9]IEEE Std 647，IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros，IEEE Inc．，2006，1－83．

[10]任亚飞，柯熙政．基于阿伦方差的微机电陀螺误差建模及其粒子滤波[J]．中国计量学院学报，2009，20(2):102－106．