徐州某大跨空间结构抗震性能分析

李俊

【摘要】徐州某空间结构跨度大，结构体系复杂，钢柱长度，给其抗震性能设计带来困难。本文建立上部钢结构单独模型和钢结构——混凝土裙房整体模型进行分析对比，研究地震作用下混凝土裙房对于上部钢结构动力响应的影响。根据该结构体系特点，结合国内外设计规范确定该结构的抗震性能目标，为该结构设计与分析提供理论依据和数据支持。本文结论可为复杂空间结构的抗震设计和地震响应分析提供参考。

【关键词】大跨空间结构；下部结构影响；层间位移角；抗震性能设计；弹塑性时程分析

1. 结构概况

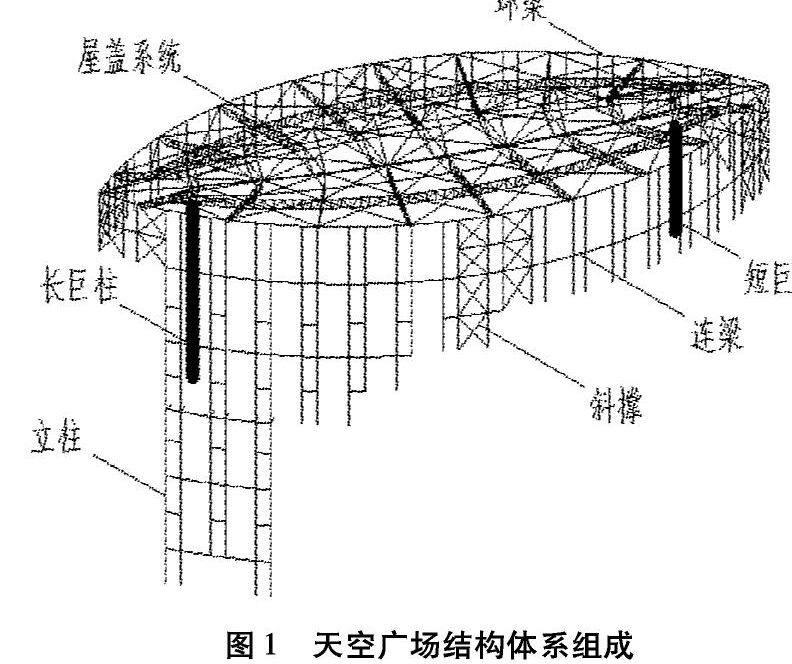
（1）徐州某综合体屋盖建筑坐落于徐州市中央商务区，钢结构屋盖的平面形状为对称梭形，长轴106m，短轴53m，屋盖檐口高出裙房屋顶8.7m，结构体系如图1所示。天空广场屋盖的竖向荷载通过内部两根巨型钢管混凝土立柱和周边框架柱传至其下部裙房结构，天空广场钢结构的抗侧和抗扭刚度，由支撑和顶环梁与钢柱形成的支撑框架结构提供。该结构体系复杂主要体现为：钢柱长短不一，刚度中心和质量中心不重合；钢结构支承于下部混凝土裙房之上。

图1天空广场结构体系组成

（2）目前，考虑下部支承结构影响的分析方法主要包括整体建模分析方法和简化分析方法。简化分析方法仅对上部模型进行单独分析，根据刚度等效、阻尼等效和质量等效的原则，对分析结果进行修正，以减少分析过程的计算量^[1～5]。这些简化方法尚不能考虑下部支承刚度对上部结构地震响应的影响，且计算精度较低。本文通过整体建模与简化模型分析比较，研究下部裙房结构对上部钢结构地震反应影响的程度，并对比国内外规范性能化抗震设计的要求，制定该结构具体的性能化设计目标。

2. 性能目标

2.1性能目标的选择。

（1）性能化设计是当今抗震设计的发展趋势，世界各国设计规范设防水准和性能目标的确定准则不尽相同。我国现行《建筑工程抗震设防分类标准》GB50023^[6]和《建筑工程抗震形态设计通则》CECS160^[7]采用三等级设防水准， ASCE41^[8]则采用四等级设防水准，GB50023与CECS160对应的设防水准定义基本相同。本文按照GB50023和CECS160的水准一确定多遇地震水平，按照水准三确定设防地震水平，按照GB50023和ASCE41的水准四确定罕遇地震水平。

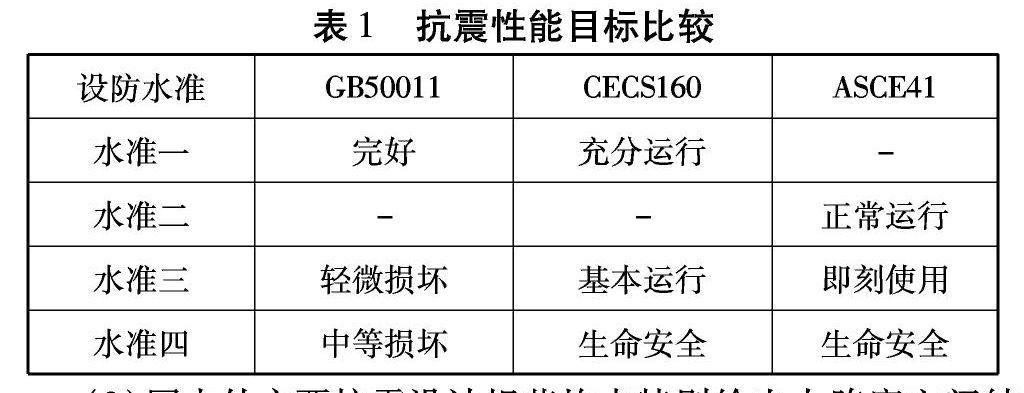
（2）CECS160^[7]的性能目标选择按重要性分四级，ASCE41则分为三级。本工程应归为CECS160中的II类建筑或ASCE41中的震灾关键建筑。GB50011、CECS160和ASCE41中相应的性能目标比较见表1。

（3）国内外主要抗震设计规范均未特别给出大跨度空间结构设计的具体控制指标，本文根据钢结构类构件定义其控制指标（表2）。

2.2结构变形及构件承载能力限值。

目前，多高层结构变形设计的控制指标主要为层间位移角，对于复杂大跨度空间结构，层间位移角的定义没有意义。但对于天空广场钢结构设计，为控制P-Δ效应，可参照多高层结构设计按框架整体侧移确定层间位移角，以防止结构变形过大导致玻璃幕墙等非结构构件破损或坠落，该结构的层间位移角应考虑钢柱长度不同和扭转变形两种因素。由于天空广场钢结构和下部混凝土裙房的刚度相差较大，可以认为不同长度的钢立柱其柱顶和柱脚的位移差是一定的，因此，高度较小的钢柱会产生较大的层间位移角（图2a）。对于扭转效应明显的椭圆形屋盖，角部变形将超过中部变形（图2b），鉴于此，本结构的层间位移角可偏于安全地定义为较短角柱的柱顶柱脚位移差与该柱柱高之比。在确定构件承载能力抗震性能目标时，将结构构件分为主要构件和耗能构件两类。主要构件包括巨柱、主次桁架、外围立柱和环梁，耗能构件包括支撑和环梁。本结构性能目标的控制指标见表3。

图2结构变形模式与层间位移角定义

3. 结构计算模型

（1）结构整体计算模型柱脚采用刚接约束，天空广场单独计算模型落地长柱采用刚接约束，其他均采用铰接约束模拟。钢结构和钢筋混凝土结构框架采用梁单元，钢筋混凝土板采用壳单元。钢材采用Q345B，混凝土为C35～C55，材料本构关系采用抗震设计规范推荐的多线性随动强化模型。计算多遇地震响应时，单独模型阻尼比钢结构取0.03，整体模型取0.035；计算罕遇地震响应时，两种模型均取0.05（钢材本构关系见图3、混凝土本构关系见图4）。

（2）时程分析时采用的多遇地震波峰值加速度为35cm/s2，罕遇地震波峰值加速度为220cm/s2，分别将X方向和Y方向作为主输入方向，主方向、次方向和竖向的地震波峰值比为1：0.85：0.65. 多遇地震波时程曲线见图5和图6。

4. 结构自振特性

（1）本结构整体属于剪切型结构，上部屋盖钢结构属于轴力型结构，整体结构和上部钢结构的振型均比较复杂，高阶振型效应可能较大。计算需保证两个结构模型各个方向的质量参与系数累积量均超过90%，篇幅所限仅将部分自振周期及质量参与系数值列于表4（单独模型前三阶振型见图7，整体模型前三阶振型见图8）。

图7单独模型前三阶振型

（2）结构单独模型的自振模态表明，竖向振动和扭转在前几阶振型中就开始显露，且存在平扭耦联现象，高阶振型贡献很大；而结构整体模型的自振模态中，前几阶振型以平扭耦联振动为主，竖向振动在70阶振型以后才出现。

（3）比较两种计算模型的计算结果可看出，钢结构单独模型和钢结构混凝土整体模型的自振特性差异很大，且两者之间并无明显关联。对于结构整体模型而言，其前几阶振型更多地表现为混凝土裙房的自振特性，这表明下部混凝土裙房对于上部钢结构振动特性影响不可忽略。

5. 地震作用响应分析

5.1分析方法。

本文采用弹性时程分析得到结构在多遇地震和设防烈度地震下的动力响应，采用弹塑性时程分析法得到罕遇地震下的动力响应。弹性时程分析时选择CQC组合的模态积分法；弹塑性时程分析选择逐步积分法。根据结构构件的受力状况，弹塑性时程分析时采用轴力——双向弯矩耦合铰（P-M-M铰）。

5.2分析结果。

结构变形的验算结果列于表5，构件的承载能力验算结果如表6所示。结构层间位移角和屋盖挠跨比时程曲线如图9所示，应力最大构件位置如图10所示，罕遇地震下塑性铰出现位置如图11所示。

5.3结构抗震性能评价。

（1）地震作用下，两种计算模型结构变形和构件承载能力均满足抗震性能目标的要求，其中单独模型结构变形远小于整体模型，且不同地震水平作用下，构件应力差异不大，这表明采用单独模型，地震效应被低估。

（2）罕遇地震作用下，单独模型所有构件保持弹性；整体模型由于承受较大侧向力作用，部分连梁和支撑构件屈服，结构共10处出现塑性铰，其中P铰1处，P-M-M铰9处。进入塑性的构件占构件总数的0.62%，结构整体进入弹塑性工作状态，耗能构件发挥作用，但结构整体变形和关键构件应力均在限值范围内，该结构具有良好的抗震性能。

6. 结论

（1）该结构两种计算模型的动力特性差异显著。对于复杂结构体系，忽略下部结构的影响，仅对上部结构进行动力分析结果并不准确。

（2）根据国内外设计规范，本文从结构变形和构件承载能力两方面制定结构的抗震性能目标。采用按较短角柱侧移和屋盖挠跨比控制结构变形。多遇地震、设防烈度地震和罕遇地震作用下的侧移限值依次为1/250、1/125和1/50，多遇地震下挠跨比限值为1/250。构件承载能力性能目标为：多遇地震、设防烈度地震作用下，构件保持弹性；罕遇地震作用下按构件分类控制，主要构件保持弹性，耗能构件允许屈服但不破坏。此性能目标可以反映结构的安全要求且可操作性强。

（3）罕遇地震下，耗能构件进入塑性阶段，结构体系合理，抗震性能满足要求。

参考文献

[1]李金龙， 空间结构与下部结构协同工作简化分析方法研究， 2009， 天津大学.

[2]陈应波， 陈军明， 网壳结构与下部结构协同工作的研究. 华中科技大学学报（自然科学版）， 2004（3）： 第49～50+53页.

[3]曹资等， 网壳屋盖与下部支承结构动力相互作用研究. 空间结构， 2001（2）： 第19～26页.

[4]刘成军， 网壳结构与下部支承体系协同工作的研究， 2005， 东南大学.

[5]建筑抗震设计规范（GB50011-2010）. 北京： 中国建筑工业出版社， 2010.

[6]建筑工程抗震设防分类标准（GB50223-2008）. 北京： 中国建筑工业出版社， 2008.

[7]CECS160-2004， 建筑工程抗震形态设计通则， 北京： 中国计划出版社.

[8]American Society of Civil Engineers. Seismic rehabilitation of existing buildings. Reston： ASCE/SEI 41-06， 2007.

[9]汪大绥等， 复杂结构弹塑性时程分析在ABAQUS软件中的实现. 建筑结构， 2007（5）： 第92～95+12页.

[10]罗永峰， 杨木旺， 大跨度刚性空间结构地震反应的静力弹塑性分析方法. 建筑科学与工程学报， 2008（3）： 第73～80+114页.

[11]罗永峰， 王磊等， 罕遇地震下上海中心超高层的性能化抗震设计. 同济大学学报（自然科学版）， 2011（4）： 第467～473+613页.

[12]谢开仲， 大跨度钢管混凝土拱桥非线性地震反应分析与研究， 2005， 广西大学.

[13]林家浩， 张亚辉， 赵岩， 大跨度结构抗震分析方法及近期进展. 力学进展， 2001（3）： 第350～360页.

[14]刘尚伦， 大跨度张弦桁架结构弹塑性地震响应分析， 2008， 太原理工大学.

[15]范峰， 空间网壳结构弹塑性地震响应及抗震性能分析. 哈尔滨建筑大学学报， 1999（1）： 第32～37页.

[16]程绍革， 王理， 张允顺， 弹塑性时程分析方法及其应用. 建筑结构学报， 2000（1）： 第52～56页.

[17]黄鑫， 刘瑛， 黄河， 基于Push-over原理的SAP2000结构弹塑性分析实例. 青岛理工大学学报， 2007（4）： 第19～23页.

[18]沈雁彬， 基于动力特性的空间网格结构状态评估方法及检测系统研究， 2007， 浙江大学.

[19]曲哲， 叶列平， 潘鹏， 建筑结构弹塑性时程分析中地震动记录选取方法的比较研究. 土木工程学报， 2011（7）： 第10～21页.

[20]张笈玮， 考虑地震空间效应的大跨度空间结构抗震分析与设计方法， 2009， 天津大学.

[21]孙玉萍， 空间网架结构弹塑性时程分析的关键技术. 甘肃工业大学学报， 1998（1）： 第99～104页.

[22]吕西林， 王亚勇， 郭子雄， 建筑结构抗震变形验算. 建筑科学， 2002（1）： 第11～15页.

[23]丁阳， 张笈玮， 李忠献， 行波效应对大跨度空间结构随机地震响应的影响. 地震工程与工程振动， 2008（1）： 第24～31页.

[24]裴星洙等， 日本抗震规范中有关地震力和输入地震波的处理方法. 建筑结构， 2007（8）： 第78～81页.

[25]沈麒， 杨沈， 中日建筑抗震规范抗震设计比较. 工程抗震与加固改造， 2012（4）： 第102～106页.

[26]吴晓涵， 原中晋， 吕西林， 上海浦东国际机场T2航站楼弹塑性时程分析. 地震工程与工程振动， 2008（4）： 第70～75页.

[27]姜锐， 苏小卒， 塑性铰长度经验公式的比较研究. 工业建筑， 2008（S1）： 第425～430页.

[28]钟万勰， 结构动力方程的精细时程积分法. 大连理工大学学报， 1994（2）： 第131～136页.

[29]储德文， 王元丰， 精细直接积分法的积分方法选择. 工程力学， 2002（6）： 第115～119页.

[30]赵岩， 林家浩， 唐光武， 复杂结构局部非线性地震反应精细时程分析. 大连理工大学学报， 2004（2）： 第190～194页.

[31]韦承基， 史铁花， 薛彦涛， 合理振型数的确定及扭转振型判定. 工程抗震， 2002（4）： 第1～2+9页.

[32]王福智， 王依群， 邓孝祥， 振型数的选取及扭转振型的确定. 天津理工大学学报， 2005（3）： 第81～85页.

[33]吴晓涵等， 上海世博会中国馆结构弹塑性时程分析. 建筑结构学报， 2009（5）： 第112～118页.

[34]王蕊， 大跨度空间结构弹塑性时程分析， 2007， 天津大学.

[35]何庆祥， 沈祖炎， 结构地震行波效应分析综述. 地震工程与工程振动， 2009（1）： 第50～57页.

[36]黄鑫， 大跨度空间结构抗震设计方法研究， 2007， 天津大学.