小学数学“解决问题”解题习惯的培养
唐丽娟
在一节新课里,同一类型的题目有相对应的解题方法,靠死记硬套公式也可以答对。当题目稍微改变,学生却一片茫然。原因在于学生没有养成良好的解题习惯,不能真正理解题意和里面的数量关系。因此,教师在解决问题课堂教学中不但要传授解题方法,还要重视培养学生良好的解题习惯,否则,学生的解决问题能力不但得不到提高,还不利于学生数学应用意识的养成。
“无论是什么类型的问题,其核心都是需要学生通过观察、思考、猜测等富有思维成分的活动才能解决的。”因此,可以培养学生以下几方面的解题习惯,提高学生的解决问题能力。
一、正确的审题习惯——观察
审题要做到“三部曲”即“读——动口,想——动脑,划——动手”相结合的三次读题。解决问题往往是在生产生活中的实际问题情境,生活化的语言与数学语言差别较大,加上语句长、叙述抽象的特点,使得学生对题意的理解往往产生困难。学生第一次读题目就要从具体情境里发现数学问题,找出数学信息有意识地重点读。第二次读题要重视数学语言的表达,让学生把题目的条件、问题逐一表述出来,使学生对题目的结构意义达到正确的理解。例如:把一些日常生活中常见的数量概括成数学术语,如时间、速度、路程;单价、数量、总价等等。为了促使学生在读的同时加强感知,第三次读题,培养学生在关键的、重要的字词下面“用铅笔画”做标记的习惯。例如:分数与百分数解决问题题目中用直线划出单位“1”的量,圈出已知条件与问题中不统一的数量单位,找出隐蔽的已知条件,去掉多余的已知条件等等。
二、画图分析题目的习惯——思考
在解决问题教学中,有些教师只在黑板帮助学生画图,不要求学生学会画图,学生没有想象发挥的机会,体验不到将抽象的实际问题转化为具体形象的数学问题这一重要环节。一般情况下,许多类型的问题而言,图形表征是发现解决问题方法的一种有效手段。当学生遇到不会解的题目时,通过以下画图方法加深理解题意,在涂涂画画中有可能找出解题方法。
1.画实物图。低年级的解决问题,往往都是以小动物、花果等编题,教师在教学和作业中,可以要求学生按照题目画实物图,再分析列式解答,这样学生不仅得到画画的乐趣,同时也可以得到正确分析解题的方法。在高年级里画实物图有助于把问题化繁为简。例如:鸡免同笼的问题,如果使用画实物图的方法,学生容易理解。先按照题目数量画出动物头,然后每个头添两只脚(因为无论是鸡还是兔都会有一个头和至少两只脚),再把剩下的脚每两只添到一个头上,添上两只脚的头数就是兔子的数量。
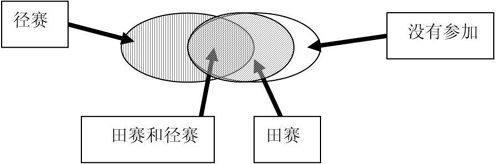
2.示意图。到了中、高年级,数字比较大,题目难度也加深了,可以用示意图取代实物图帮助学生依靠直观的感知进行抽象思维。例如:三(1)班同学参加学校运动会,参加田赛的有26人,参加径赛的有30人,以上这两项都参加的有12人,这两项都没参加的有4人,问全班有多少学生?
通过示意图,数形结合感知情境问题,把多个的已知条件转化为的直观表象,学生容易想出多种解题方法:
解法一:26+30-12+4=48(人)
解法二:26+(30-12)+4=48(人)
解法三:26-12+30+4=48(人)
解法四:(26-12)+(30-12)+12+4=48(人)
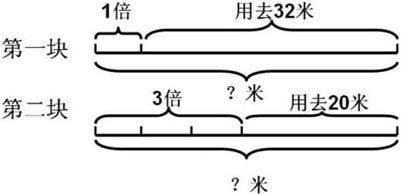
3.画线段图。苏霍姆林斯基指出:“画线段图不仅是表象和概念加以具体化的手段,也是一种使学生进行自我智力教育的手段。”线段图在小学数学应用题教学中起到了奇妙的作用,它可以帮助学生轻松、愉快的学会复杂关系的应用题,是教学中行之有效的教学方法。例如有两块同样长的布,第一块用去32米,第二块用去20米。结果第二块所剩的米数是第一块的三倍,两块布原来各长多少米?
从线段图容易找出解题的关键:第一块布比第二块布多用去的正好是第一块布剩下的(3-1)倍。
解法一:(32-20)÷(3-1)+32
= 12÷2+32
= 38(米)
解法二:(32-20)÷(3-1)×3+20
= 12÷2+32
= 38(米)
三、比较归类的习惯——猜测
比较归类出运用相同知识点解答的题目,对表述相近的题目或有多种解法的题目进行比较,抽象概括出事物的本质特点,学会分类、总结其规律,能够最快地找出解题策略,使解题能力得到提升。例如:归类出分数和百分数这类型的解决问题,遇到这种题型,首先找单位“1”的量、分量、分率,然后判断问题求什么?根据等量关系式“单位1的量=分量÷分率,分量=单位1的量×分率,分率=分量÷单位1的量”解题。
总之,教师在数学教学活动中重视学生良好解题习惯的养成,使教学效果事半功倍,提高学生的解决问题能力和数学思维能力,变“学会”为“会学”,为终身学习打下坚实基础。

