如何判定相似的三角形

尼玛次仁

在初中教学中证明图形的相似度是我们教学中的重点，也是在以后的教学中学习“三角形”和“圆”的基础，对于相似三角形的判断必须要熟练而灵活，本文笔者简单的阐述了

相似三角形判定，供参考。

一、判定两个三角形相似的基本定理.

1、如果两个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

2、如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。

3、如果两个三角形的三组对应边的比相等，那么这两个三角形相似。 .

二、相似三角形最基本的图形需熟练掌握

1、A型，直线D E截两边可得 4个三角形与原AA B C相似.

2 、X型，直线D E截两边延长线可得2个三角形与原AA BC相似.

3、公共角

因此，两个相似三角形经过平移、 旋转、 翻折后依然相似.

4、两个全等的三角形一定（肯定）相似。

5、两个等腰直角三角形一定（肯定）相似（两个等腰三角形，如果其中的任意一个顶角或底角相等，那么这两个等腰三角形相似）

6、两个等边三角形一定（肯定）相似。

7、直角三角形相似判定定理

（一）斜边与一条直角边对应成比例的两直角三角形相似。

（二）直角三角形被斜边上 的高分成的两个直角三角形与原直角三角形相似，并且分成的两个直角三角形也相似。

三、三角形判定的例题分析

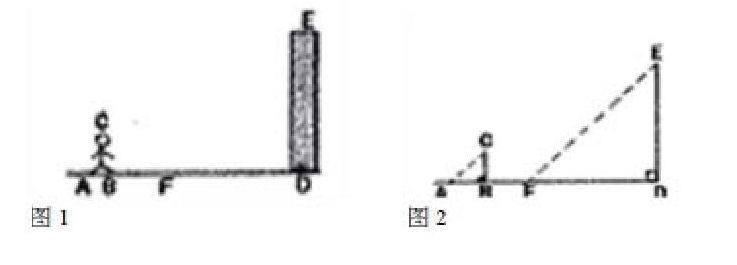
例在一次数学活动课上，老师带领学生去测教学楼的高度，在阳光下测得身高1.6 5 m的甲同学的影长 BA为 1.1 m， 与此同时， 测得教学楼的影长 D F为 1 2 .1 m， 如图1所示。请你根据已测得的数据，求教学楼 DE的高度。（精确到0.1m）

图1 图2

分析：这里我们把太阳光看作为平行光线， 即如图2中的AC与EF互相平行， 于是本问题可以转化在?ABC和?FDE中，利用 AC∥EF证得?ABC∽?FDE.由相似三角形对应边成比例可以求出DE的长。

解： 如图2

∵AC∥EF

∴∠CAB=∠EFD

又∵CB⊥AB，ED⊥FD

∴∠CBA=∠EDF=90°

∴?ABC～?FDE

∴BC/DE=BA/DF

即1.65/DE=1.1/12.1

∴DE≈18.2（m）

因此，教学楼DE的高度约为18.2m.

点评：本题目借助相似三角形的性质解决实际问题，关键是寻找二角形相似的条件，利用太阳光是平行光以及人、楼与地难亩画出相应的图形构造相似三角形，然后通过相似三角形对应边成比例得出关系式求解。

综上所述，判定三角形相似的方法较多，同学们要灵活选择，明确判断的思路，关键是能分析题 目提供的已知条件，充分去寻找要判断相似三角形所缺的条件，灵活而准确地组成三角形相似的条件。