两千年前的数学奇迹

王纲怀

在铜镜这个特殊的文物载体上，华夏祖先创造了世界数学史上的奇迹。通过本文，我们可以穿越时空去寻觅：两千年前为等分圆周的国人，在用尺规作图时，对数字特别是素数的情怀、喜爱、探索、挑战。

高斯（1777年至1855年）是德国著名的大数学家、物理学家、天文学家，他是近代数学奠基者之一，在历史上影响之大可以和阿基米德、牛顿、欧拉并列。他在少年时代就对欧几里德作图理论产生了浓厚的兴趣，1796年3月30日，终于发现了正十七边形（正十七边形之数字17，是素数系列中的一个。要在圆周上用尺规等分除3、5以外的素数，迄今仅由高斯解决了17等分，其他素数在目前皆属不能解决的数字难题。素数亦称“质数”。大于1的整数，除了它本身和1以外，不能被其他正整数所整除的，称为“素数”。）的尺规作图（初等平面几何只研究直线形和圆以及由它们组合而成的图形，并且限定以直尺和圆规为作图的工具。）法。他曾要求在他去世以后，能将正十七边形刻在他的墓碑上。虽然这个要求未被满足，但是在高斯出生地布伦瑞克为他建立的纪念碑底座上有一个正十七边形，应该说正十七边形的尺规作图是数学王子高斯一生成就的奠基石。1855年2月23日，高斯在哥廷根天文台逝世之后，汉诺威王命令为高斯制作一个纪念章，上面镌刻有“献给数学王子”的字样，从那以后，高斯就以“数学王子”著称于世。

殊不知，早在1700年至2300年前的中国铜镜纹饰面上，就已经出现了包括素数17在内的一个圆周等分的数字系列。由此，我们会惊奇地发现，华夏祖先在数学领域上的伟大创造力。

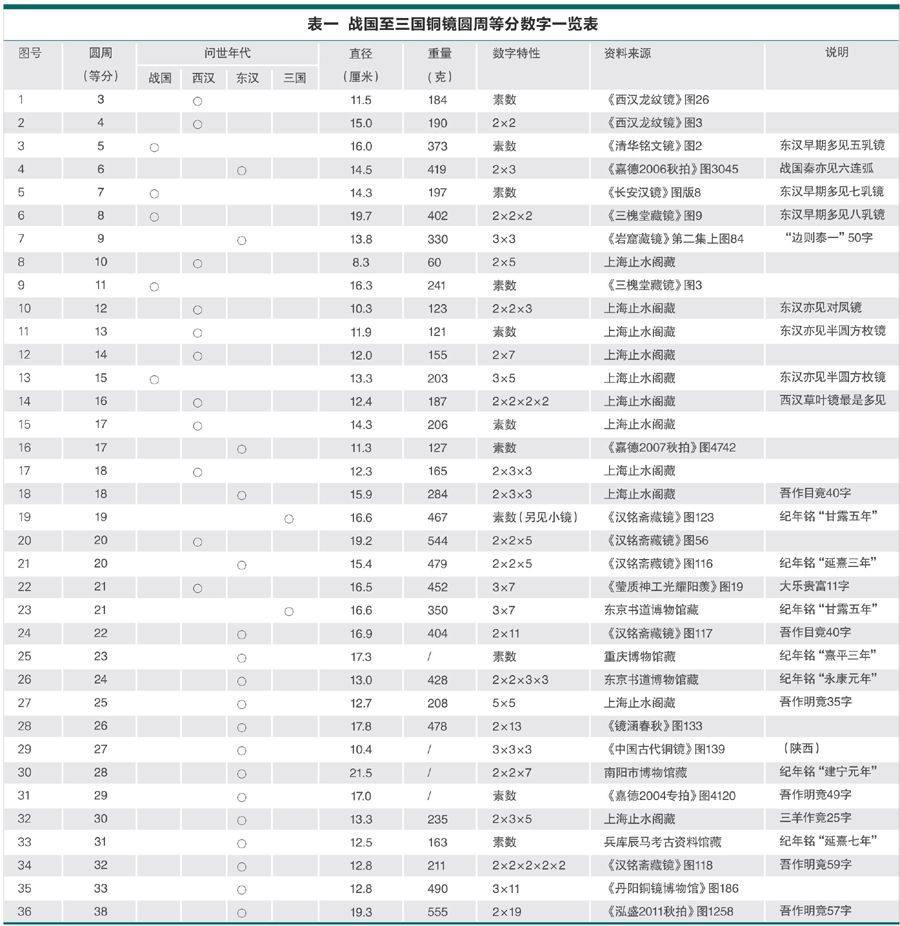
在二十余年的收藏经历中，笔者时有发现：从战国至三国的600年间，中国古代铜镜有着诸多不同的圆周等分数字。经过多年的寻觅查找，癸巳之春，终于找全了从3到33这些数字的连续系列（详见表一）。

一、据表一可知，数字18（含18）以下者共有18个，按年代与主纹分，有以下多种：

1.战国——三龙连弧镜（如：图13为15连弧）

2.战国——五山镜（如：图3为5等分）

3.战国——素地连弧镜（如：图9为11连弧）

4.战国秦至西汉——蟠螭纹连弧镜（如：图5、6为7、8连弧）

5.西汉早中期——龙纹镜（如：图1、2为3、4等分）

6.西汉早中期——连弧镜（如：图10、11、12、14、15、17）

7.西汉早中期——草叶镜、圈带镜（连弧多见16，少见18、20）

8.东汉早中期——多乳神兽镜（乳钉可见5、6、7、8，数字9仅现钮区）

9.东汉晚期——连弧镜（如：图7为9连弧）

二、据表一可知，数字19（含19）以上者共18个，多见于东汉三国，少见于西汉。

1.数字19、20、21重复见于西汉、东汉、三国魏。

2.迄今所知，数字22（含22）以上者，多在东汉变形四叶兽首镜之中。

3.存世还见大于33的连弧数，如：38（图36）、48、62等。

三、据表一可知，数字17至21为过渡区，不同的年代皆有出现。

四、新莽时期几乎皆为四灵博局镜，似不见有圆周等分的情况。

在表一的36个数字系列中，共有3、5、7、11、13、17、19、23、29、31等10个素数。其间，数字3、5可以用尺规解决，数字17已被德国大数学家高斯破解，还剩7、11、13、19、23、29、31等7个素数，不知汉人如何解决？目前，只能是“知其然而不知其所以然”。我们猜想，即使古人可以用“近似法”这样既简易又繁琐的原始方法，然亦保存了汉人面对不同素数这诸多数学难题的历史记录。

战国晚期至三国魏共约600年。在铜镜这个特殊的文物载体上，华夏祖先创造了世界数学史上的奇迹。通过本文，我们可以穿越时空去寻觅：2000年前为等分圆周的国人，在用尺规作图时，对数字（特别是素数）的情怀、喜爱、探索、挑战。