浅谈“形数转换”在数学中的应用
2013-04-29 20:47:08黄振海
新课程学习·下 2013年7期
黄振海

数学解题是从不同角度解决问题,在遇到一些图形推理试题时,很多学生就转不过弯来,这时如果我们将图形问题转换成数字问题,就可以达到事半功倍的效果。
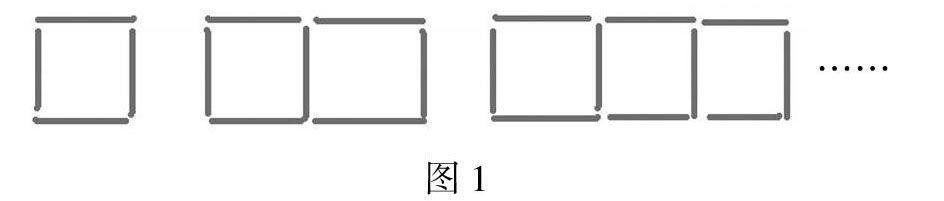
例如:北师大版七年级数学《字母能表示什么?》这一节中讲到:
如图1所示,搭1个正方形需要4根木棒,搭2个正方形需要7根火柴棒,……如果用x表示所搭正方形的个数,那么搭x个这样的正方形需要多少根火柴棒?
我们通常的做法是:
方法1:第一个正方形用4根,每增加1个正方形增加3根,那么搭x个正方形需要火柴棒为[4+3(x-1)]根,化简得:(3x+1)根。
方法2:上面的一排和下面的一排各用了x根火柴棒,竖直方向用了(x+1)根火柴棒,共用了[x+x+(x+1)]根,化简得:(3x+1)根。
这样绕来绕去,很多同学都绕晕了,如果我们换个方法,将图形转变为数字,看看效果怎样:
(注:变形时要观察后一个与前一个数之间的关系)
即将图形问题转变成了数字推理题,很快就推出第x个图形需要(3x+1)根火柴棒。这个题很简单,用方法一、方法二都好解决。所以,培养学生的转化能力是数学解题策略中不可忽视的重要方面,这个题很简单,如果遇到复杂的,“形数转化”这种方法就表现出了很多优点。
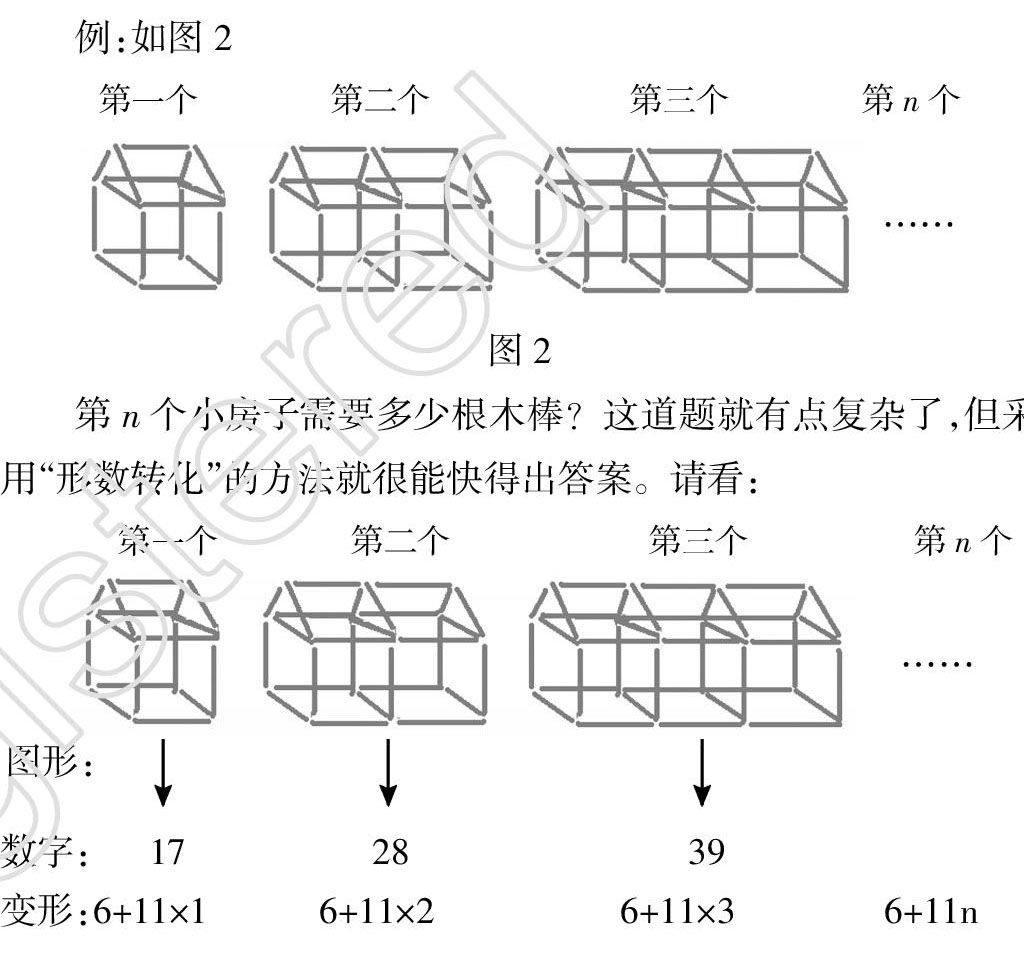
例:如图2
第n个小房子需要多少根木棒?这道题就有点复杂了,但采用“形数转化”的方法就很能快得出答案。请看:
你看,很快就得出了第n个图形需要(11n+6)根木棒。
以上是本人在教学中的一点小小收获,希望能与大家分享。
(作者单位 贵州省六枝特区木岗镇中学)
猜你喜欢
数学小灵通(1-2年级)(2024年1期)2024-05-14 09:20:44
小学生学习指导(高年级)(2022年10期)2022-11-04 06:20:50
小天使·一年级语数英综合(2020年5期)2020-12-16 02:56:26
作文周刊·小学二年级版(2019年21期)2019-08-09 03:08:47
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:54
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
红蜻蜓·低年级(2015年1期)2015-03-26 10:39:56
小朋友·快乐手工(2014年2期)2014-02-25 12:19:03

