加强图意解读，确保话语系统的起始教学

何霞

人教版教材第一学段应用问题的编排创设了学生喜闻乐见的教学情境和现实活动，以图文并茂的形式生动活泼地呈现，让学生感到这些问题都来自自己熟悉的生活原型，以期达到激发学习兴趣，促进学生发现问题、提出问题、解决问题的目的。教材编排精美，编者愿望美好，然而教者教学时却疑云重重，困难多多。

现象扫描

课例1 （一年级上册第47页）求剩余部分的减法问题

题意：画面上共有7个向日葵，摘取了3个，还剩几个？

学生列式：4+3=7。因为左边有4个，右边摘取了3个，共有7个向日葵。

课例2 （一年级上册第58页做一做）求去掉部分的减法问题

题意：画面上共有7只鹅，还剩3只，走了几只？

学生列式：7-4=3。因为7只减去走掉的4只等于剩下的3只。

现象分析

学生混淆数学信息与数学问题，主观寻找数学信息、数学问题的意识淡薄等是错因所在。教材图中，主要以“？”的位置来确定信息和问题，课例1与课例2都是学生在不明确哪是数学信息、哪是数学问题的情况下，解题时错误地将问题“还剩几个”“走了几只”等数量当信息用，导致计算方法错误。图中信息与问题不是学生可随意认定的，也不可能随学生的意愿更改的。信息就是信息，问题就是问题，学生怎么将信息与问题混为一谈的呢？

1.客观因素

教材中要求问题的数量在情境图中清晰可数，是导致学生不分信息与问题的客观原因。图画问题是以图画形式出现，图中不光已知的数量可数，而且要求问题的数量也清晰可数。如课例1中问题是“还剩几个”，但“剩余部分”画面上却清楚地画着“4个向日葵”。课例2问题是“走了几只”，但“走掉部分”画面上却清楚地画着“4只鹅”。由于画面中问题的数量清晰可数，所以学生无法理解到底什么是信息、什么是问题。

2.主观因素

学生缺乏寻找信息问题的意识，思维定势与负迁移等是导致学生不分信息与问题的主观原因。

如教学“减法问题”时，由于前面加法图画问题“左边……右边……一共……”的读图思路，给学生减法问题的读图造成了思维定势与负迁移，同时学生又不主动思考题中信息是什么、问题是什么，这种情况下，学生也按上述加法思路读图，“左边有4个向日葵，右边摘取了3个向日葵，一共……”于是就想当然地列出加法算式了。又如课例2“求去掉部分”，学生受减法含义“去掉几就要减去几”的负迁移，就按“总数-去掉部分=剩余部分”的数量关系找寻“总数与去掉部分”两个信息进行解答，导致解题错误。

像这样学生缺乏寻找信息问题意识、思维定势与负迁移等原因混淆信息问题，导致学生解题错误的不在少数。

由此可见，第一学段应用问题教学中加强图意解读，培养学生收集信息、提出问题的能力，确保话语系统的起始教学，是图画问题教学的重要任务，也是今后进一步学习应用问题的基础。

策略探寻

在当今信息社会中，从纷乱的实际问题中收集、观察、比较、筛选有用的信息，抽象成数学问题，这是学生正确解决问题的重要前提。“良好的开端是成功的一半”，低段图画应用问题如何加强图意解读、收集信息、提出问题，确保话语系统的起始教学呢？下面就此谈一点想法。

1.看清图意，界定两个概念

在应用问题的教学中，经常会提到“数学信息”“数学问题”两词，那么“数学信息”“数学问题”为何物呢？数学课中的“数学信息”是指问题情境中告诉我们的有关数学的信息，“数学问题”是指要回答或解释的有关数学的问题。一年级上册第47页“加法问题”图意：左边捉蝴蝶的有4人，右边捉蛐蛐的有2人，是图画中告诉我们的“数学信息”。图中大括号下面第一次出现的“？”表示问题“一共有几人”就是所要求的“数学问题”。在课堂上多设置这样的问题：这幅图告诉我们的“数学信息”是什么，要求的“数学问题”是什么？以此帮助学生界定概念，有效解读图中的“数学信息”与“数学问题”。这样坚持不懈地训练，培养学生自觉界定“数学信息”与“数学问题”的习惯，为学生进一步解决问题埋下伏笔。

2.借助媒介，规范有序地表述

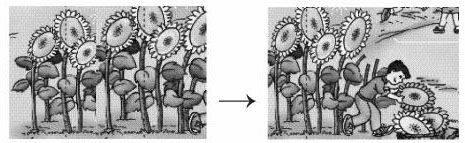
低段人教版教材“解决问题”的编排注重用学生熟悉的感兴趣的现实活动和事例设计情境，通过图文并茂的形式生动活泼地呈现学习资源，但是由于主题图以静态方式呈现丰富的内容，这样给学生表述图意，解读“数学信息”“数学问题”带来一定困难。教学时教师不妨将情境图制作成动画课件，也可以逐步板贴等，让学生随着教学流程的推进，随着课件或板贴的动态演示逐步说出图意，引导学生正确理解画面内容所表达的意思，引导规范有序地表述“数学信息”和“数学问题”。如课例1的教学，可以运用课件，先出示图1，再出示图2（如下图），随着课件的演示，教师引导学生有序地说出“数学信息”与“数学问题”：“你看到了什么”“又看到了什么”“你能提出什么数学问题”，引导学生先说出2个信息“一共有7个向日葵”“摘下了3个”，再说1个问题“还剩几个”。

→

图1 图2

通过课件的逐步演示，逐一出现信息、问题，这样就去掉了图中无关的信息，提取有用的数学信息与问题，有利于帮助学生规范有序地表述“信息”和“问题”，确保学生数学语言系统的完整性。当然，随着年级的升高，解决问题中信息与问题之间的关系逐渐复杂，语句的叙述要求也越来越高。

3.由图及文，建立结构模型

建立应用问题的结构最有效的途径是指导学生学会有序看图、读图，寻找相关联的信息，提出问题，并将它以文字的形式表示出来。图画应用问题是文字应用问题的重要基础，将图画应用问题抽象成文字表述形式：2个数学信息与1个数学问题，有利于帮助学生建立良好的应用问题结构，有利于帮助学生做好由图画问题到文字问题的过渡。

如教学课例1“求剩余的减法问题”时，在课堂上让学生完整地说说信息与问题，随着学生的回答教师跟进板书，将三句话在黑板上写下来（如下图）。通过这样的教学可以帮助学生完整地表述信息与问题，同时帮助学生建立应用问题的一个基本结构（2个数学信息与1个数学问题）。

数学信息：一共有7个向日葵，摘走了3个。

数学问题：还剩几个向日葵？

由“图”及“文”，“图”“文”结合的教学，让学生在图画问题学习中就对应用题的框架有一个整体感知，播下了应用问题结构的“种子”，有利于确保学生数学语言系统的完整性，也有利于学生理清解题思路，为今后正式学习文字问题打下基础。

4.互换信息，防止思维定势

为了使学生熟练解读图意、收集信息与提出问题，防止思维定势，感知“信息”和“问题”的相对性，教学时可多进行在同一幅图中进行信息与问题转换的训练。

通过变换信息转换问题，使学生明白：信息与问题不是一成不变的，是可以转换的。适时转换信息与问题，有利于打破思维定势，有利于提高学生解读图意、收集信息、提出问题的能力，有利于感知“信息”和“问题”的相对性，也有利于学生进一步全面理解加减法的含义以及它们之间的联系与区别。

如“求去掉部分的问题”，它是学生学习中的难点，教材中又没有安排专门的例题，学生理解这个问题的解题思路有一定的困难。互换信息与问题的“题组”训练，有利于学生理解这类问题。

要求学生说说每题的已知信息与问题，可以是学生自由说、指名说，待学生正确区分每一题的已知信息与问题后，组织学生对各题的数量关系展开分析、比较、判断、推理，让学生在潜移默化中懂得审题的重要性。题组训练，有利于学生把握信息与问题，确保话语系统的完整性，也为学生选择合理的、正确的解决问题的方法与策略打下必要的基础。

5.口说手演，理清数量关系

《数学课程标准》（2011年版）在“解决问题”的教学目标中强调：“要让学生能表达解决问题的过程，并尝试解释所得的结果。”由此可见，培养学生能用简单的数学语言有层次地表达思考问题的过程与结果，是解决问题的教学中的一个重要方面。图画问题，教材中虽然没有编写解题的思路，但教师教学时还应该注重学生说解题思路的训练。由于一年级学生以具体形象思维为主的特点，训练说解题思路时，可采用口说手演等形式帮助学生理清解题思路、理解数量关系。如教学“加法问题”时，教师可以带领学生边手势操作边口述：如伸出左手——表示捉蝴蝶的有4人，伸出右手——表示捉蛐蛐的有2人，然后“左右手合拢”——表示合起来求“一共有几人”，打手势的同时口述：“左边的4人与右边的2人合起来，就是一共的人数，要用加法计算。”实际上，学生说理的过程也就是学生分析解题思路的过程。口说手演有利于帮助学生把注意力集中于问题的突出方面或关键因素，给学生留下了深刻的印象，有利于帮助学生寻找解题思路，强化数量关系，也有利于确保学生数学话语系统的完整性。

图画应用问题中加强图意解读，加强规范有序表述问题信息、解题思路与数量关系，确保话语系统起始教学是新课程下数学应用问题教学的一个重要内容，也是学生今后学习解决应用问题的重要基础。因此，需要教师在应用问题的教学中长期地、坚持不懈地对学生进行相关训练，还需要在其他课型如计算教学等中加以渗透训练，尽可能确保学生数学话语系统的完整性，以真正提高学生收集信息、提出问题、分析数量关系、解决问题等能力。