浅析初中数学如何有效实施数学建模

张惠芬

随着时代的进步，数学的学习方法日新月异.而在初中数学中，数学教育日益着重培养学生的创新和应用能力.“数学建模”是很好的一种学习方法，它把生活案例转变成了形象的数学问题，然后去建立相应的数学模型以解决实际问题，很好地培养了学生的思维能力.现笔者就数学建模谈谈几点体会.

一、 从数学教材出发，结合生活实际，实施数学建模

数学建模应从正常的教学内容的切口进入，以教育的教材为载体，通过加工教学中的数学问题，激发学生的学习兴趣和欲望，让学生在用中学、学中用.让他们在知道数学的解析方法的同时，也能学到数学的精神和思想.

与此同时，在日常生活中，很多问题都可以通过建立数学模型（数学建模）去解决.只要结合数学课程的内容和联系生活实际，适时引导学生进行数学建模，就能够加深学生对数学问题的理解和深入思考.

例如，在教完学生不等式的“比较法”后，可结合实际生活设置如下题目，引导学生进行数学建模以解决问题.

问题：6个苹果和7包瓜子的价格之和小于35元，而8个苹果和5包瓜子的价格大于36元，则2个苹果和3包瓜子哪个更贵呢？

分析：对于这个实际问题，设每个苹果的价格是x元，每包瓜子是y元.那么那个抽象的数学问题就会转换为形象的实际问题，并得出两个条件6x+7y<35，8x+5y>36，比较2x和3y的大小，即作差：2x-3y即可得到答案.

通过这样的方法，学生很好地理解了抽象的数学问题.

二、精选典型例、习题，彰显数学建模过程

中学中的数学建模主要是要控制在“简单应用”和“部分复杂”这二者结合的水平上.在教学中，教师应适当将一些难度不大的题，提供给学生一些数学建模的体验，和他们一起完成数学化的过程.

下面以实验教材（苏科版七年级、八年级）为例.

【例1】 用乘法公式计算（x+4）³.

分析：题目有一定的难度.根据算式，很容易就可以看出算式是要求三个（x+4）相乘，那么由于只学过二次方程，可以把式子转换成（x+4）²（x+4）进行计算，然后套用公式（a+b）²=a²+2ab+b².在计算过程中，须注意算数的正确.

解：原式=（x+4）²（x+4）

=（x²+8x+16）（x+4）

=（x³+8x²+16x）+（4x²+32x+64）

=x³+（8x²+4x²）+（16x+32x）+64

=x³+12x²+48x+64

此题不仅提高了学生对于数学公式的灵活运用，更让学生在计算过程中能够更谨慎细心.

【例2】

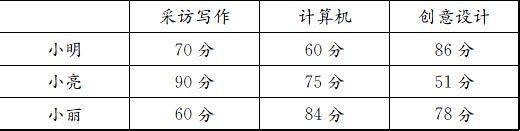
某报社要招聘一名记者，小明、小亮和小丽报名参加了三项素质测试，成绩如下表.

（1） 如果根据三项测试的平均成绩确定录用人选，你选谁？（小丽被录取）

（2） 根据实际需要，报社给出了选人标准，将采访写作、计算机和创意设计三项测试得分按5∶2∶3的比例确定各人的测试成绩，那么谁将会被录取？（小亮被录取）

（3） 如果按3∶2∶5的比例计算，谁会被录取？（小明被录取）

分析：（1）根据平均数的计算公式：x=（x_a+x_b+x_c+…+x_n）÷n得出结果.

（2）（3）将每个人的三项成绩分别乘以相应的比例再除以比例的和计算出结果，再相比较结果大小得出答案.

解析略.

（2）（3）问就是“加权平均数”的典型例题.通过以上日常生活中熟悉的素材作為例题，让学生了解到平均数与加权平均数的区别和联系，能够正确辨别两者.从模型应用角度来说，假设再多出两位应聘者或者改变了比例，又该怎样去算呢？

三、概述结合实际后的趣味数学模型

通过例题分析，建立起相应的数学模型，从猜想到解答并验证的这一过程，都能让学生在生活的感受中去解答，更重要的是数学模型留给了学生很多的想象空间，使得原本看似枯燥无味的数学变得生动有趣.

但是在很多时候，教师会过多关注如何让学生通过建模解决数学问题，而忽略了数学建模本身能让学生发挥更多的素质和能力这一特点.为此，每位教师都应发掘身边生活的点滴，利用这些生活的有效资源去激发学生对数学的热爱，让学生感受数学的无穷魅力，同时发展他们自身未被发现或已发现的优势.

（责任编辑 黄春香）