带有时间窗的食品车指派问题研究

王 琪，唐小卫，栗鹏举

(1．南京航空航天大学民航学院，江苏 南京 211100;2．北京省都国际机场服务有限公司技术采购部，北京 100621)

机场机坪作为飞机地面保障作业的场所，其保障设备能否得到及时、有效的利用直接影响到机场服务的质量和效率。据统计，由保障服务引起的航班延误占大型枢纽机场所有航班延误的15．45%［1］，因地面保障设备调度不佳而造成的延误是造成航班延误的原因之一。为了使保障服务的控制更具效率，改进航班过站地面保障服务的工作调度势在必行。

航食配餐环节是当前航空公司地面保障的关键环节，这体现在:①配餐作业与其他作业流程衔接紧密，作业时间限制严格。与配餐相互联系的作业包括旅客下机(下机之后才能开始)、旅客登机(登机之前必须完成)和客舱清洁(回收毛毯、卫生用品等)。如衔接不当，则会增加地面保障时间，甚至造成航班延误。②食品车是地面保障车辆设备中唯一需要不断地往返于场内和场外的设备。③整个作业耗时受加、减餐环节影响较大。如果加餐车及时到位，这一环节只需要几分钟。实际运行中因为需求的不确定性，导致加餐车的数量不定，且有可能在入口门处排队等待的时间过长，以致于食品车经常不能够及时到位，造成航班延误。

食品车调度作为机坪保障服务设备调度的重要环节之一，其调度过程非常复杂。首先，天气突变、设备故障、航班延误等突发性和随机性因素不可避免，导致计划服务时间与设备实际服务时间不一致［2］;其次，在食品车服务的过程中，食品车调度要遵循相关的行业规范，即有相对确定的服务时间限制和操作顺序。如为了保证配餐质量及飞机安全，食品车的行驶路径及速度固定，不得随意更改，即食品车在机坪的作业时间很难缩减;再者，食品车的服务需求时间离散分布，最终的登机人数很难确定，导致所需食品车数量的不确定性。因此，食品车调度问题是一个带有时间窗和作业调整时间的多目标作业动态排序问题［3］。

航食公司是典型的高成本和低利润的企业。为了提高航食公司的竞争力，降低运行虚耗成本是使其收益增加的有效方式之一，建设行之有效的餐食配送系统是降低成本的一种重要手段。为了优化航班与食品车二者的组合，通过建立带有时间窗的食品车指派模型，减少行驶过程中的虚耗成本，并给出相应求解算法，最后用实例验证。

1 带有时间窗的食品车指派模型

1．1 食品车指派问题

所谓食品车指派问题，是指在给定的作业时间窗内，考虑航班时刻、机型、食品车数量，以及食品车行驶路径等因素，指派食品车为纯进港航班回收餐车、纯出港航班加餐、过站航班回收餐车，以及加餐等操作，它是地面保障的重要环节之一。食品车指派结果包括指派给航班的食品车编号和食品车保障各航班的时间。

食品车指派是经典指派问题的一种变形，其中被指派者是食品车，任务是需要食品车作业服务的航班。由于作为任务的航班明确了完成时间，这就决定了食品车指派不同于经典指派问题，是带有时间窗的，因此航班的食品车指派比经典指派问题更为复杂。

1．2 相关假设及变量设定说明

1．2．1 相关假设

为了研究食品车指派问题，假设某航空公司只有一家航食公司代理保障进出港航班的餐食作业，并将所有航班按纯进港、过站、纯出港分类。对纯进港航班只进行餐车回收作业;对纯出港航班只进行加餐作业;对过站航班既要进行餐车回收作业，也要进行加餐作业，而其作业顺序一般是先回收后加餐。

在这里需要强调的是，对于过站时间短的航班，食品车在进行回收作业后直接执行加餐操作;而对于过站时间长的航班，为了保证餐食的时效，先回收餐车，在其离港前再为其指派食品车进行服务，因此可以将其拆分成纯进港与纯出港航班，分别建立食品车指派模型来求解。

1．2．2 约束说明

为保证机场正常安全运行，应给出食品车指派基本约束条件，其基本约束主要包括:

(1)机型与食品车数量相互匹配约束。一般C、D类飞机需要1辆食品车，E类飞机需要2辆食品车，F类飞机则需要3辆食品车同时作业。食品车的容量固定，一般可装载30辆左右的餐车。除了食品车数量与机型相匹配外，还要根据订座人数确定餐食份数，以减少虚耗成本。这就出现了食品车的一次循环作业，一次循环作业航班数与航班类型有关，小机型航班需要的航食少，作业时间短，反之则长。一次循环的时间包括从航食公司基地到第一个作业机位的行驶时间、加餐作业时间、两机位之间的行驶时间、从最后一个作业机位返回航食公司基地的行驶时间、在航食公司的回收清洗时间和装载食品时间。

(2)某一时段，一辆食品车只能为一个航班服务。

(3)一辆食品车可保障多个航班(一次循环)。

(4)满足时空衔接要求，即对于进港航班，飞机进港靠桥后开始食品车作业，对于出港航班，要在旅客登机前完成作业，以保证航班能顺利进出，避免造成航班延误。

1．2．3 变量设定

给每个进港航班按照进港时刻编号1，2，…，n，并构成航班集合I，航班到达次序I={i|i=1，2，…，N}，在航班进港后，会有唯一的停机位与其对应，因此上述编号既是航班编号，也是停机位编号。在集合I上定义参数Ai，Di和Li分别表示航班i的进港时刻、出港时刻和机型，将机型按从小到大的次序编号 1、2、3、4，分别代表 C、D、E、F 4类机型。同时给各食品车编号j=1，2，…，m构成食品车集合J，在集合J上定义各类机型所占食品车数量类型Cj，将满座时服务最大机型所需食品车数量定义为食品车的类型，按类型从小到大编号1、2、3、4，分别代表 C、D、E、F 类机型所占食品车数量。当Li≤Cj时，航班i可由食品车j服务。

指派周期是指将机场一天的运行时间划分成若干区间。确定每个周期长度的原则是，该周期内新到港过站时间长的航班不在本周期内出港，出港的是在期初已进港或本周期进港且过站时间短的航班，过站时间长短的标准根据各机场不同标准而定，其表现为回收餐车与加餐是否同时进行。在每个周期的开始，食品车集合J分成3个子集J0，J1和J2。J0为空闲的食品车集合，J1为正在服务航班的食品车集合，J2为本周期中可以空出可服务其他航班的食品车集合，J2为J1的子集，其中J2食品车数量可通过餐食服务人员的通报获得。该周期需要处理的航班集合也分成3个子集I0，I1和I2。I0为本周期初始时刻已在机位上且将在本周期内出港的航班，I1为在本周期即将进港的航班。在I1上定义两个子集I2与I3:I2为过站时间短即在本周期内出港的航班，I3为过站时间长且在后续周期中出港或不再出港的航班，即I2的回收餐车与加餐是同时进行的，I3为纯进港航班。I0与I2可以通过查询航班离港时刻获得。

1．2．4 模型建立

由于食品车指派涉及食品车的行驶距离、航食公司的经济效益、机场资源的利用效率，以及地面服务部门的工作场所等多个方面，因此从不同的角度考虑会涉及不同的目标函数。为了使所建模型更符合实际，采用航班等待时间和食品车行驶时间之和最小为目标函数，并根据基本约束条件建模分析。食品车在机坪上的作业时间固定，为了节约运行成本，对航班和食品车二者组合进行优化。因此给出一个周期中食品车指派问题的数学模型如下:

对于过站时间短的航班，其航班等待时间以离港前索取资源时刻为标准。下面将J0或J2的食品车指派给航班I2。取航班等待时间与食品车行驶时间之和最短为目标函数，则有:

对于纯进港航班，将上述模型中的I2变为I3即可。

对于纯出港航班，将J0或J2的食品车指派给航班I0，式中的Ai则表示航班i索取资源的时间，I2变为I0，其余不变。

对于过站时间长的航班，可将其拆分成纯进港与纯出港航班分别建模求解。

式中，Z0为食品车准备时间，即本周期的期初时刻;Zi为占用时间;Kj为食品车j∈J0∪J2可指派给下一个航班服务的开始时刻;xij为决策变量，当i航班指派给j食品车时等于1，否则等于0。式(7)计算的Kj为已知参数，由于占用食品车时间可通过服务人员通信获得，tij可通过指派后的路径及食品车行驶速度计算得出，作为该周期的初始条件，对于j∈J1的食品车和i∈I0的航班，xij的值已知。

在该模型中，目标函数式(1)中第一项为航班等待时间，第二项为食品车行驶时间，(·)+表示当括号中的值大于零时等于括号中的值，否则等于零。约束条件式(2)表示必须为本周期内进港的航班指派相应类型数量的食品车进行服务，s为服务食品车的数量。式(3)表示同一时刻，每种类型的食品车最多可指派给一个航班。式(4)表示只有空闲食品车(期初空闲或被释放的食品车)才能与航班相互指派。式(5)表示只有机型不比食品车类型级别高的航班才可以与该种类型的食品车相互指派。式(7)表示对于行驶回基地的食品车的可再指派的开始时刻=它的前一航班占用食品车时间+食品车的返回行驶时间+准备时间;而不回基地直接服务于后续航班的食品车开始时刻，即为其为上一航班服务的结束时刻。由此，上述模型满足了所有基本约束。

对于上述模型可采用航班连接树构造供食品车指派的可能航班串，然后优化选择指派，具体步骤可参考文献［4］。在找到各食品车所有的航班串之后，可以建立的食品车指派模型如下:

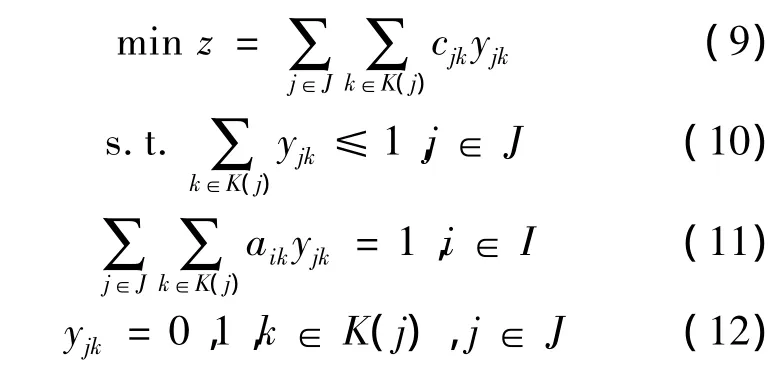
上述模型中，I和J分别为航班集合和食品车集合，K(j)为j号食品车的航班串集合。cjk为j号食品车的第k条航班串的空闲时间和延误时间的总和，aik=0，1，当航班串k包含有航班i时等于1，否则等于0，yjk是0－1决策变量，如果航班串k指派给j号食品车，则等于1，否则等于0。

2 求解算法

求解式(9)～式(12)可以获得每辆食品车一天的指派计划。但求解这组模型是困难的，经典指派问题的匈牙利算法已不再适用求解上述模型。文献［5］建立了带有时间窗的车辆路径问题(vehicle routing problem with time windows，VRPTW)模型，证明了VRPTW是一个非线性规划(non-linear problem，NP)疑难问题，该问题的最优解是难求解的。文献［6］提出了三下标车辆流方程，该方程是针对带时间窗口、无停留时间，以及能力约束的VRP的;并基于Benders的分解算法，提出了一种启发式算法，保证在有限的步骤内找到优化解。文献［7］将车辆行驶时间最短和配载最大为优化目标，把时间窗引入约束限制，研究车辆配送与配载的两目标优化调度模型组，并用仿真实现。文献［8］用分枝定界算法解决了一类带时间约束指派问题，并用实例及算法复杂性分析证明该算法是有效的。文献［9］用贪婪模拟退火算法求解枢纽机场停机位指派模型，并用实例仿真进行验证。文献［10］为取得任意两架飞机之间的水平约束，提出航空器相对于飞行高度层的一般性指派问题的研究方法，还给出了当效率矩阵随条件发生变化时，将不确定性问题转换成确定性问题处理的一般方法。

分析上述模型，由约束式(10)可知，对任一组可行解，决策变量矩阵中，每一列向量有且仅有一个元素为1，其余元素均为0。针对这一特征，可以采用列生成算法和分枝定界法求解。列生成法适用于变量数远大于约束条件数的问题，基变量数相对于非基变量是较小的一部分。如果预先能确认可行的基变量，就可以令其他变量等于零，使问题的规模大大减小。根据这一特点，可以先用分枝定界法得到可行的基变量，再用列生成算法进行迭代，以获得最优解。

给出一个定义:已知该问题的一个可行解为X，则称B*=Z(X)为该问题的一个界。设矩阵为j号食品车的第k条航班串的空闲时间与延误时间之和矩阵，则算法步骤如下:

(1)初始化，即给定初始可行解。分枝定界算法的有效性在很大程度上取决于界的确定，该问题的界为已得到的可行解的目标函数值。给出一组较好(即使尽可能小)的初始可行解，以得到一个能快速收敛的界。

(2)任意选择主问题的几条路径，构成限制主问题，求其最优解，可获得式(10)和式(11)的对偶变量。将矩阵中的各元素减去式(11)的对偶变量，构成子问题，再求其最短路径，将该最短路径的长度减去式(10)的对偶变量，即可获得主问题的非基变量的最小简约时间。如果其大于等于零，限制主问题的最优解即为原问题的最优解;若其仍小于零，则生成该路径的列，将该最短路径加入主问题，生成新的限制主问题，用热启动再求其最优解。

3 算例

在浦东机场，某食品公司每天保障约380个客、货运出港航班，其中约90个国际和地区航班，食品公司共运营40辆食品车，日常有35辆提供保障服务。每辆食品车一次循环保障2～4个航班，一天保障7～9个航班。高峰小时保障出港航班38个。中航与外航分开保障，笔者以外航食品车为例，进行验证。

该机场近机位从6到24号是E类(分类号为3)，其他近机位是D类(分类号为2)。两相邻E类机位之间食品车行驶距离为72．5 m，两相邻D类机位之间为59．5 m，D类与E类机位相邻的距离为66 m。场内食品车直线行车速度不超过40 km/h，转弯行车速度不超过15 km/h，接近航空器行车速度不超过5 km/h。为了简化求解过程，可用食品车的平均行驶速度25 km/h来计算求解。食品车服务过站航班C、D、E、F类机型的平均时间分别为 25 min、30 min、45 min、55 min，纯出港航班分别为 15 min、20 min、30 min、40 min，纯进港航班分别为 10 min、15 min、20 min、25 min。

外航在某调配周期内有11个进出港航班，由8辆食品车保障。该调配周期内航班计划如表1所示，其中STA为计划进港时刻，STD为计划离港时刻;无进港航班号表示纯出港航班，无出港航班号表示纯进港航班。食品车指派结果如表2所示。

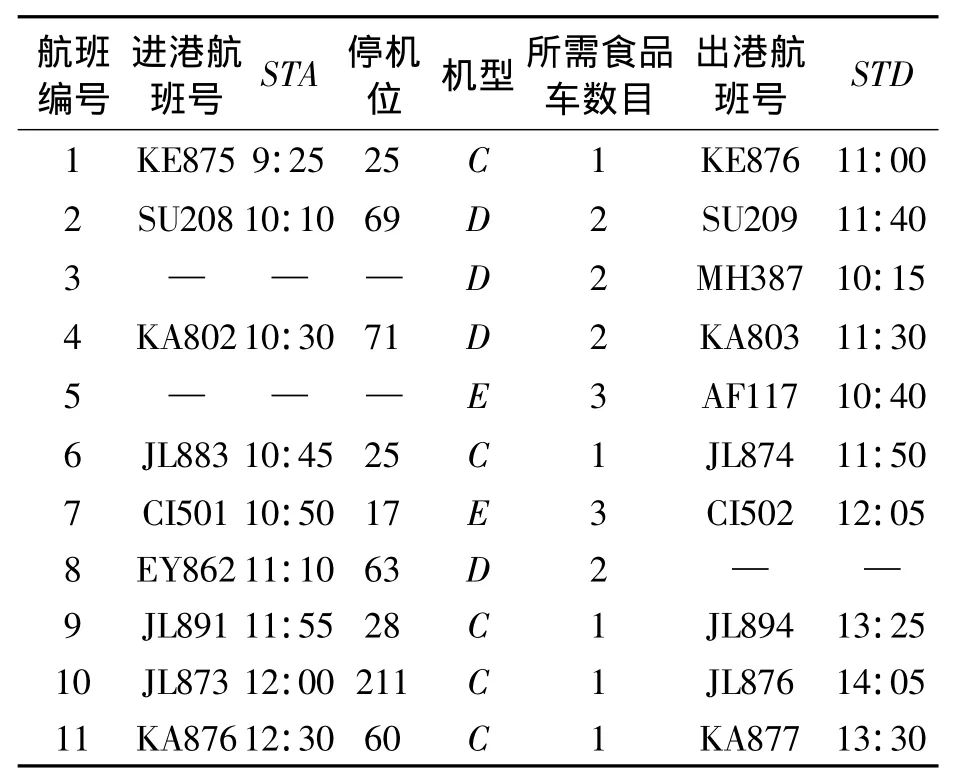
表1 浦东机场2013年某日航班计划信息(给定周期内)

从结果中可以得出，航班等待时间与食品车行驶时间之和为78．31 min，比实际时间之和93．68 min减少了16．4%，说明该算法可行有效。

表2 食品车指派结果

4 结论

为优化航班与食品车二者的组合，提高食品车使用效率，以航班等待时间与食品车行驶时间的和最短为目标函数，建立带有时间窗的食品车指派模型，并给出相应求解算法，从而达到降低航空公司成本的目的。最后，用实例证明该算法是可行有效的。但是，笔者尚未考虑加餐车作业，需要进一步深入研究。

［1］ 朱金福．航空运输规划［M］．西安:西北工业大学出版社，2009:528-532．

［2］ AHMET B．Procedures for providing robust gate assignments for arriving aircraft［J］．European Journal of Operational Research，2000，120(1):63 －80．

［3］ 姚韵，朱金福．航班过站地面服务的优化调度算法［J］．信息与控制，2007，36(4):486 －492．

［5］ SAVELSBERGH M．Local search for routing problem with time windows［J］．Annals of Operations Research，1985，16(4):285 －305．

［6］ FISHER M L，JAIKUMAR R．A generalized assignment heuristic for vehicle routing［J］．Networks，1981(11):109－124．

［7］ 杨锦冬，徐丽群．城市物流中心车辆配送配载调度指派模型研究［J］．同济大学学报，2004，32(11):1453－1456．

［8］ 李引珍，郭耀煌．一类带时间约束指派问题的分枝定界算法［J］．系统工程理论与实践，2005(6):39－42．

［9］ 鞠姝妹．枢纽机场停机位指派的算法优化与仿真［D］．南京:南京航空航天大学图书馆，2008．

［10］ 牟奇锋，王慈光．高度层优化使用问题的指派模型及算法［J］．电子科技大学学报，2009，38(4):573 －577．