基于梯形需求率的变质物品库存模型
潘义前,黄 海,周优军
(1.广西民族师范学院 数学与计算机科学系,广西 崇左 532200;2.柳州师范高等专科学校 数计系,广西 柳州 545004)
产品的市场生命周期是指一种新产品从进入市场到被市场淘汰的整个过程.一般地,产品的市场生命周期可以分成四个阶段,即引入期、成长期、成熟期和衰退期.在产品的引入期和成长期,市场对产品的需求越来越大;在成熟期,市场对产品的需求比较平稳;在衰退期,市场对产品的需求有下降的趋势.许多文献对处在成长期、成熟期或衰退期的产品库存问题进行了研究,需求率分别假设为常数、线性函数或指数函数.例如,经典EOQ库存模型,其需求率是常数;文献[1]建立了Ramp型需求且允许缺货的库存模型;文献[2-4]研究了Ramp型需求、变质率是常数的库存模型;文献[5]探讨了需求率为一般Ramp型函数、变质率是Weibull函数、缺货量部分拖后的库存问题,并给出了确定最优订货策略的算法.上述文献的需求函数只是刻画了产品处在成长期和成熟期的需求变化,而没有把产品处在整个市场生命周期的需求变化情况描述出来.文献[6]假定物品的需求率为一般形式的梯形需求率函数,变质率为二参数的Weibull函数,采用允许缺货且缺货部分拖后策略,缺货量拖后率是等待时间的递减函数,建立了变质物品EOQ模型;文献[7]在连续支付方式下,研究了零售商两阶段延期支付的最优经济订购批量问题;文献[8]采用线性梯形函数刻画产品生命周期的需求变化情况,建立了不允许缺货的库存模型.文献[9]改进了文献[8]的结果,引进一般梯形函数表示产品生命周期的需求变化,假设物品的变质率是时间的线性函数,允许缺货且缺货量拖后率是递减的指数函数.
采用先缺货的库存策略可以减少物品存贮管理费用,但是有可能产生丢失销售机会[5].本文根据产品在生命周期需求变化的特点,用一个一般的梯形函数来表示需求率,即需求率在开始的一段时间是递增函数,然后在另一个时间段内是常数,在某一个时间点之后,需求率随时间推移而逐渐减小;假设物品的变质率是时间的一般函数,建立了先缺货后订货、缺货量拖后率是等待时间的减函数的库存模型.目的是优化库存系统总成本,并证明了总成本最小值的存在性及唯一性,给出了最优订购策略的算法步骤.
1 符号说明与假设
1.1 符号说明
I(t)表示在时刻t的库存水平,其中,t∈[0,T],T表示产品生命周期长度(常数);t1表示订货的时间点(决策变量);S表示一个周期的最大正库存水平;c1和c2分别表示每单位时间单位物品的库存维持成本和缺货成本费;c3和c4分别表示每单位物品的变质成本和由于失去销售而产生的单位物品的机会损失成本.
1.2 模型假设
库存状态图如图1所示.
(1)假设库存系统在开始时间[0,t1]内发生短缺,短缺时部分需求拖后,在t=t1时刻进行订货,订货量为Q,受需求和变质的影响,库存在[t1,T]内逐渐减少,在t=T时库存为零.
(2)瞬时补货,订货提前期为零.
(3)需求拖后率β(x)是等待时间x的函数,β(x)满足如下条件:
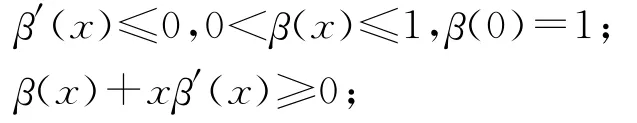

其中,θ(t)为变质率.
(4)考虑单一变质物品,变质率θ(t)是时间t的连续函数,需求率D(t)是梯形函数:

其中,
f1(λ)=f2(μ),f1(t)>0,f′1(t)>0,f′2(t)<0.

图1 库存状态图Fig.1 Diagram of inventory state
2 模型建立
以下分0≤t1<λ,λ≤t1<μ与μ≤t1≤T三种情形求出库存总成本.
情形1 若0≤t1<λ,则此时库存水平I(t)的变化应满足如下微分方程:

解上述微分方程得
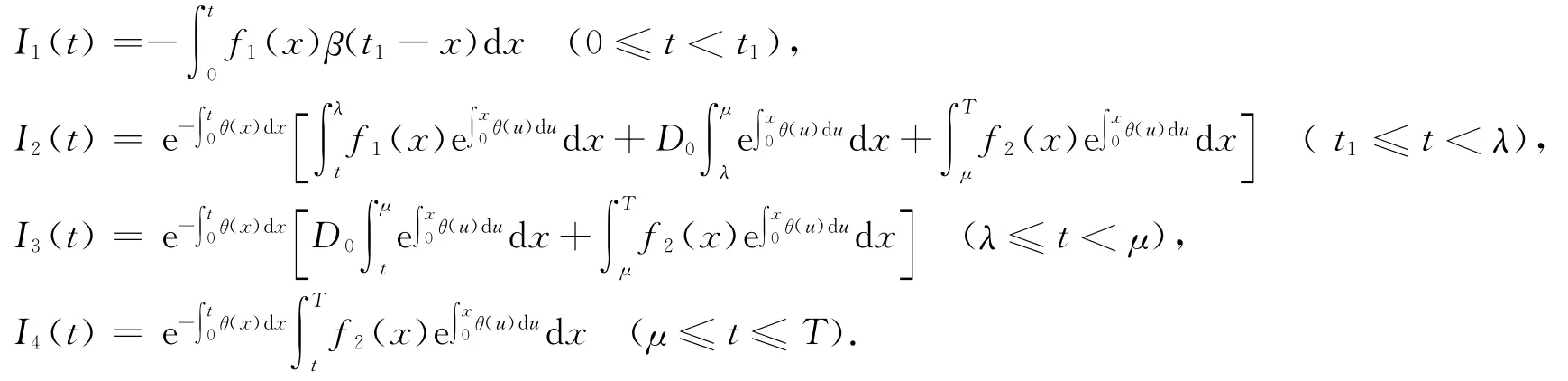
于是,在[t1,T]内,物品变质的总量D及物品的库 存总量H 为

由于短缺时部分需求拖后,因此,在[0,t1]需求拖后的总量B及失去的销售量L为
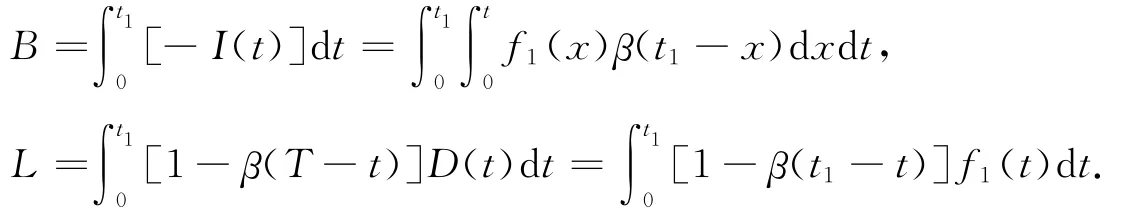
因此,在一个计划期[0,T]内,库存总成本TC1(t1)=库存维持费+缺货损失费+变质损失费+机会损失费,即

情形2 若λ≤t1<μ,类似于情形1,可以得到一个计划期[0,T]内的总成本TC2(t1)为

情形3 若μ≤t1≤T,类似于情形1,可以得到一个计划期[0,T]内的总成本TC3(t1)为

因此,在计划期[0,T]内,库存系统的总成本函数为

于是,本文的库存模型为

3 模型求解
为了便于讨论函数TC(t1)在[0,T]上最小值的存在性,令 A(t1)=c1θ(t1)-c3θ′(t1)+c3(θ(t1))2,H(t1)=c2β(t1-t)+c2(t1-t)β′(t1-t)-c4β′(t1-t),于是得到如下结论.
引理 方程TC′(t1)=0在(0,T)内至少有一个解.
证明 分别对TC1(t1),TC2(t1)与TC3(t1) 求关于t1的导数得

则有

其中

由式(9)知,函数TC(t1)的导数TC′(t1)在[0,T]上连续;根据模型假设(3)可知 H(t1)≥0,从而有

显然

根据零点定理知,方程TC′(t1)=0在(0,T)内至少有一个解.
定理 如果A(t1)≥0,H′(t1)≥0,则函数TC(t1)在(0,T)内有唯一的最小值点t*1.
证明 因为A(t1)≥0,H′(t1)≥0,所以,函数TC1(t1),TC2(t1)和 TC3(t1)的二阶导数分别为

因此,在(0,T)内,TC″(t1)>0,即TC(t1)为凸函数.根据引理,可知 TC(t1)在(0,T)内有唯一的最小值点t*1.
4 最优订购策略的算法
根据定理,可以得到确定最优订购策略的算法.
第1步 输入参数,根据式(10)与式(11)分别计算Δ1和Δ2的值.

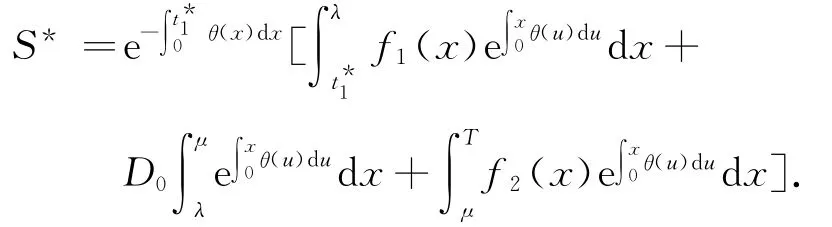
(Ⅱ)如果Δ1<0,则
① 当Δ2≥0时,根据式(7)求方程TC′2(t1)=0的解t,根据式(2)得最小总成本TC()=TC2(t*1).最优正库存S*为

最优订购量Q*为
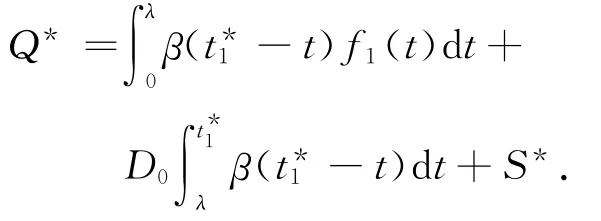
转向第3步.
② 当Δ2<0时,根据式(8)求方程TC′3(t1)=0的解t*1,根据式(3)得最小库存成本TC()=TC3(t*1).最优正库存S*为
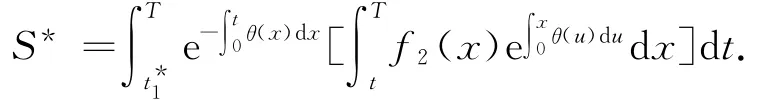
最优订购量Q*为
转向第3步.
第3步 停止.
5 数值算例
例 假设c1=2,c2=6,c3=3,c4=8,需求函数为

θ(t)=0.002t,β(x)=e-0.2x,T=1.其余参数λ,μ,a,b如表1中所示,应用 Matlab 2007计算,得最优订购策略如表1所示.

表1 例的计算结果Table 1 The calculation results of the example
6 结 语
本文采用一般的梯形函数表示需求率,建立了一类先缺货后订货、缺货量拖后率是等待时间的减函数的库存模型,其中假设物品的变质率是时间的一般函数.证明了模型存在唯一的最优解,并给出了确定最优订货策略的算法步骤.
[1] Mandal B,Pal A K.Order Level Inventory System with Ramp Type Demand Rate for Deteriorating Items[J].Journal of Interdisciplinary Mathematics,1998 (1):49-66.
[2] Manna S K ,Chaudhuri K S.An EOQ Model with Ramp Type Demand Rate,Time Dependent Deterioration Rate,Unit Production Cost and Shortages [J].European Journal of Operational Research,2006(171):557-566.
[3] Deng P S,Lin R H J,Chu P.A Note on the Inventory Models for Deteriorating Items with Ramp Type Demand Rate[J].European Journal of Operational Research,2007(178):112-120.
[4] Panda S,Senapati S,Basu M.Optimal Replenishment Policy for Perishable Seasonal Products in Season with Ramp-type Time Dependent[J].Computers & Industrial Engineering,2008(54):301-312.
[5] Skouri K,Konstantaras I,Papachristos S,et al.Inventory Models with Ramp Type Demand Rate,Partial Backlogging and Weibull Deterioration Rate[J].European Journal of Operational Research,2009(192):79-92.
[6] 黄松,杨超,杨珺.梯形需求缺货部分拖后的变质物品EOQ模型[J].工业工程与管理,2009(6):56-61.
(Huang Song,Yang Chao,Yang Jun.EOQ Models for Deteriorating Items with Trapezoidal Type Demand and Partial Backlogging Rate [J]. Industrial Engineering and Management,2009(6):56-61.)
[7] 庞留勇,张振坤,郑强.连续延迟支付库存EOQ模型[J].沈阳大学学报:自然科学版,2012,24(4):58-62.
(Pang Liuyong,Zhang Zhenkun,Zheng Qiang.An Inventory EOQ Model with Continues-delay-payment[J].Journal of Shenyang University:Natural Science,2012,24(4):58-62.)
[8] Cheng Mingbao,Wang Guoqing.ANote on the Inventory Model for Deteriorating Items with Trapezoidal Type Demand Rate[J].Computers & Industrial Engineering,2009(56):1296-1300.
[9] Cheng Mingbao,Zhang Bixi,Wang Guoqing.Optimal Policy for Deteriorating Items with Trapezoidal Type Demand and Partial Backlogging [J].Applied Mathematical Modeling,2011(35):3552-3560.

