1215钢动态应力－应变行为

朱国辉，汤亨强，柯章伟，周红兵，左遥远

（安徽工业大学 材料科学与工程学院，安徽 马鞍山 243002）

切削过程中刀具磨损行为的研究和刀具寿命的预报，一直是机械加工领域研究的重点［1］.随着高速切削技术的出现，这一问题的研究愈为重要.在高速切削过程中，切削过程所产生的热量不易散发，会导致切削区域温度的升高［2］.工件温度的升高必然导致材料力学性能的改变，而材料力学性能的改变又会引起整个切削几何和切削力的变化.因此，在切削模型中，材料的流变应力计算是切削几何和切削力，直至刀具寿命预报的最为重要的参数［3］.在切削过程中，由于工件材料承受较大的应变速度和切削过程的温升，因此，材料在切削过程中的流变应力不仅仅是应变的函数，而且是应变速度和温度的函数.因此，建立工件材料的动态应力－应变行为的本构关系，即材料的流变应力与应变、应变速度和温度的关系模型，成为切削模型的关键基础.

目前，一般而言，对于材料的本构关系模型的描述主要有基于经验公式的Johnson－Cook模型［4］和 基 于 物 理 推 导 的 Zerilli－Armstrong 模型［5］.Johnson－Cook本构模型适用于描述金属材料从低应变率到高应变率下的动态行为，甚至可以用于准静态变形的分析［6］.本文基于Johnson－Cook模型，利用1215易切削钢，对通过实验方法求解本构关系中的各个参数进行初步的讨论分析，建立1215钢的动态应力－应变行为的计算模型和方法，为下一步切削模型的建立提供必要的基础.

1 实验材料和方法

实验采用工业生产的1215圆棒，化学成分如表1所示.

表1 1215钢的化学成分Table 1 Chemical composition of 1215steel%

在高速切削过程中，材料将承受较大的应变速度.但是受到实验条件的限制，高速变形实验有较大的困难.基于本文的工作是探讨建立工件材料的动态应力－应变行为模型的基本方法，因此可以采用热模拟实验进行数学模型的求解和数据的拟合分析.因此，在本文的工作中，采用Gleeble 3500热模拟机进行热变形实验，加热速度为10℃／s.分别采用4个不同的变形速率（0.1s－1，1.0s－1，10s－1，30s－1）和4个不同的变形温度（700℃，750℃，800℃，850℃）进行变形实验，得到在不同工艺条件下的应力－应变曲线.

以Johnson－Cook模型为材料动态应力－应变关系的计算模型，通过实验数据进行求解拟合，得到1215钢的动态应力－应变方程.

2 实验结果及分析

2.1 材料的应力－应变行为

对应不同应变速度和变形温度条件下的应力－应变曲线如图1～图4所示.从图中可见，材料的应力－应变曲线首先表现为加工硬化，当形变量超过一定的数值之后，由于动态再结晶的发生，材料的应力随着应变的增加而降低，即表现出所谓的加工软化，直至达到加工硬化和加工软化的平衡.材料在高温变形过程中，一方面，由于位错的运动及增殖，多系滑移造成位错间的相互交互作用，形成位错缠结而导致加工硬化；另一方面，在高温条件下，位错可以通过攀移和交滑移产生再结晶核心.当积累的形变量超过动态再结晶临界应变，则会发生动态再结晶，而导致材料发生软化［7］.两者在材料高温动态变形过程中同时进行，共同影响着材料的流变应力.这种材料的加工硬化和加工软化现象交互作用，在应变速度较低、形变温度较高时更为明显，见图1.这是因为随着温度的降低或／和应变速度的增加，材料发生动态再结晶的临界应变增加.根据热加工理论，材料发生动态再结晶的临界应变可以表达为Z参数的函数［8］：

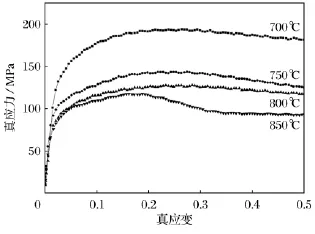
图1 应变速率为0.1s－1下的真应力－应变曲线Fig.1 The true stress－strain curve when the strain rate is 0.1s－1

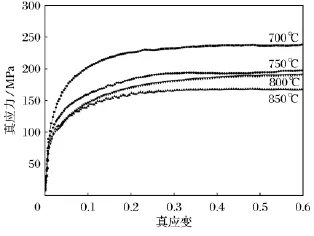
图2 应变速率为1.0s－1下的真应力－应变曲线Fig.2 The true stress－strain curve when the strain rate is 1.0s－1

图3 应变速率为10s－1下的真应力－应变曲线Fig.3 The true stress－strain curve when the strain rate is 10s－1

图4 应变速率为30s－1下的真应力－应变曲线Fig.4 The true stress－strain curve when the strain rate is 30s－1

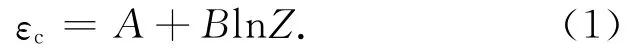
式中，Z 为 Zener－Hollomon参 数，Z＝˙εexp（Q／RT），Q为形变激活能，T为形变温度；A，B为材料常数.

从式（1）和参数Z的含义可见，随着应变速度的增加和形变温度的降低，热加工工艺过程的Z参数增加，从而导致材料发生动态再结晶的临界应变增加.这是因为在形变过程中，动态再结晶过程是一个形核长大的过程.动态再结晶核心的形成需要热激活和时间.较高的形变温度有利于位错通过攀移发生多边形化而成为再结晶核心，从而有利于动态再结晶过程的发生，表现为动态再结晶临界应变的减小.

需要指出的是，在材料的热变形过程中，除了再结晶软化效应外，随着温度的升高，由于位错运动的P－N力的减小也造成材料的流变应力减小.应变速度的提高，会导致材料的位错增殖速度加快，从而导致流变应力的增加.上述的温度和应变速度效应是材料结构的效应，而不涉及再结晶的组织演变.目前采用的Johnson－Cook模型中仅仅考虑了材料的结构变化，也就是形变温度和应变速度对P－N力和位错增殖速度的影响，而没有考虑动态再结晶的作用，也就是在采用Johnson－Cook模型进行拟合计算时，仅考虑实验应力－应变曲线的前段加工硬化部分.有关加工硬化与加工软化的交互作用将另文讨论.

2.2 1215钢的Johnson－Cook方程

根据文献［4－6］，Johnson－Cook方程的一般形式可以表达为

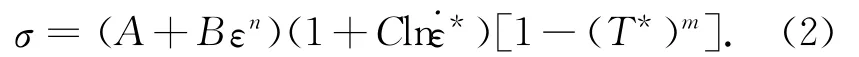
式中，σ为流变应力；ε为等效塑性应变；˙ε＊＝˙ε／˙ε0为无量纲的塑性应变速率，取˙ε0为准静态的应变速率；T＊＝（T－Tr）／（Tm－Tr），其中，T 为实际温度，Tr为参考温度，Tm为材料的熔点温度；A为在参考温度和参考应变速率下的屈服应力；B为加工硬化应变系数；n为应变硬化指数；C和m为材料常数，分别表示应变率硬化指数和温度软化指数.

Johnson－Cook模型实际上是将材料的力学行为归结为应变硬化、应变速度硬化和温度软化相乘结果的一种本构模型.在式（2）中，等号右边第一个括号的表达式给出了应变强化的作用，第二个括号的表达式给出了瞬时应变率的强化效应，第三个括号的表达式则给出了温度的软化.

2.2.1 模型中各参数的获得方法

根据目前常用的Johnson－Cook模型求解的参数识别法［9］，利用实验数据进行数据处理来取得模型中的各个参数.首先考虑模型中的加工硬化效应.以参考温度和应变速度很低条件下的应力－应变为参考，此时，式（2）等号右边第二项和第三项的影响可以忽略，式（2）简化为

式中，A为材料的屈服强度.假设参考温度为973K，以最低应变0.1s－1为参考应变，则式（3）可以变换为

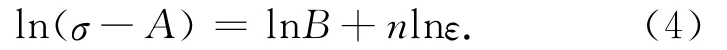
根据实验数据作出ln（σ－A）和lnε的关系曲线，曲线的截距为lnB，斜率为n，原则上可以得到参数B和n.然而，实际模拟的结果表明，由于参考温度和应变速度的影响并不能完全被排除，因此，ln（σ－A）和lnε并没有表现出预想的线性关系，如图5所示.所以，针对这种情况需要对Johnson－Cook材料本构模型作一下修正［10］，修正后的形式如下：

因此，在参考温度和参考应变速度条件下，应力和应变的关系表达式为

经过曲线拟合，可以得到各个参数为A1＝106.641 69MPa，B1＝1 129.749 56MPa，B2＝－4 108.604 49MPa.

图5 ln（σ－A）和lnε的关系曲线Fig.5 Relation between ln（σ－A）and lnε

式（2）等号右边第二项表示应变率的强化效应，参数C是材料应变率敏感系数.当塑性应变ε＝0时，由式（5）可以得到参考温度下1215钢的屈服应力和应变速度的关系.此时，Johnson－Cook材料本构模型变为如下形式：

在参考温度时

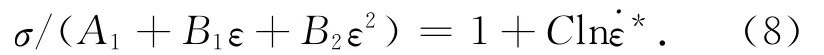
将1.0s－1，10s－1，30s－1变形速率下的实验数据代入式（8），可以得到ln˙ε＊和σ／（A1＋B1ε＋B2ε2）之间的关系，如图6所示，直线的斜率为C.采用平均拟合法得到C＝0.171 97.

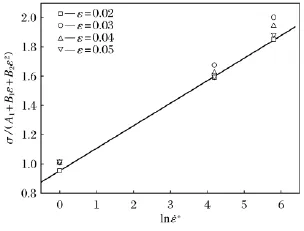
图6 ln˙ε＊ 和σ／（ A1＋B1ε＋B2ε2）的关系曲线Fig.6 Relation between ln˙ε＊ andσ／（ A1＋B1ε＋B2ε2）

在参考应变条件下，模型可以表示为

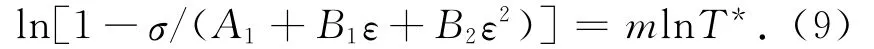
同样利用平均拟合法，可以解得m，如图7所示.

由此，Johnson－Cook模型的所有参数可以解得，分别为 A1≈106.6MPa，B1≈1 129.7MPa，B2≈－4 108.6MPa，C≈0.172，m＝0.41.

因此，得到修正的Johnson－Cook材料本构模型为

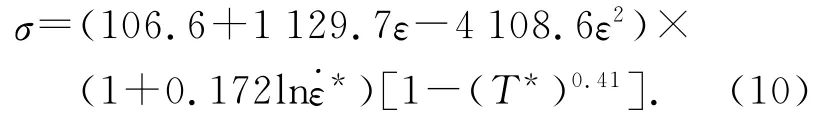
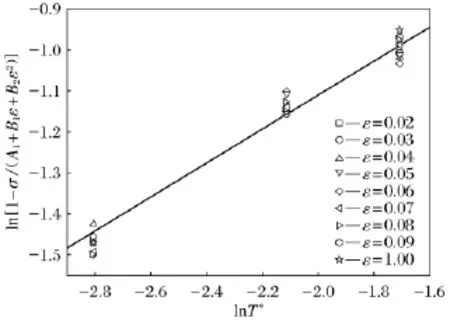
图7 lnT＊和ln［1－σ／（A1＋B1ε＋B2ε2）］的关系曲线Fig.7 Relation between lnT＊ and ln［1－σ／（A1＋B1ε＋B2ε2）］

2.2.2 实验值和模拟值之间的比较

选取700℃和800℃的实验数据与利用Johnson－Cook模型计算的数据进行比较.如前面的分析，计算数据与实验数据的比较采用从屈服到出现峰值应变前的应力－应变曲线.计算数据和实验数据比较的结果如图8和图9所示.

图8 700℃实验值和模拟值的比较Fig.8 Comparison of experimental values and analog values on 700℃

由图8和图9可见，在较低应变速度条件下，计算的结果与实验的结果得到了较好的吻合.但是对于较高的应变速度，计算的结果与实验的结果具有较大的偏差.分析图4可见，当应变速度达到30 s－1时，在热模拟实验中，实验数据出现了波纹状，这是由于热模拟试验机的限制导致大应变速度下实验结果的不稳定.因此可见，这种实验和计算数据的偏差在于原始实验数据存在较大的误差.所以有理由认为，在本文的工作中，实验的结果与Johnson－Cook方程计算的结果得到了较好的吻合.上述计算方法可用于描述材料的动态应力－应变行为.但是，有关材料在热变形过程中的加工硬化和加工软化的交互作用需要进行进一步的工作，才能完整地描述材料热变形过程的动态行为.

图9 800℃实验值和模拟值的比较Fig.9 Comparison of experimental values and analog values on 800℃

3 结 语

本文以1215钢在不同形变温度和应变速度条件下测量的应力－应变曲线为基本实验数据，以Johnson－Cook模型为材料的本构模型，探讨了利用参数识别法进行数据分析并获得1215钢动态应力－应变行为表述的数学方程.经过计算，实验结果和模型计算的结果得到了较好的吻合.

［1］ 李迎，陈维金，李小忠.基于灰色理论的高速动态铣削力在线预报研究［J］.制造技术与机床，2007（8）：13－16.

（Li Ying，Chen Weijin，Li Xiaozhong.On－line Prediction of Cutting in High Speed Milling Using Grey Theory［J］.Manufacturing Technology ＆ Machine Tool，2007（8）：13－16.）

［2］ 刘战强，艾兴.高速切削刀具磨损表面形态研究［J］.摩擦学学报，2002，22（6）：468－471.

（Liu Zhanqiang，Ai Xing. Wearing Characteristics of Cutting Tools in High Speed Machining［J］.Tribology，2002，22（6）：468－471.）

［3］ 叶贵根，薛世峰，仝兴华，等.金属正交切削模型研究进展［J］.机械强度，2012，34（4）：531－544.

（Ye Guigen，Xue Shifeng，Tong Xinghua，et al.Advances in Orthogonal Cutting Models［J］.Journal of Mechanical Strength，2012，34（4）：531－544.）

［4］ Lalwani D I，Mehta N K，Jain K.Extension of Oxley Predictive Machining Theory for Johnson and Cook Flow Stress Model［J］.Journal of Materials Processing Technology，2009，209（12／13）：5305－5312.

［5］ Lin Y C，Chen Xiaomin.A Combined Johnson－Cook and Zerilli－Armstrong Model for Hot Compressed Typical High－strength Alloy Steel［J］.Computational Materials Science，2010，49（3）：628－633.

［6］ Daridon L，Oussouaddi O，Ahzi S.Influence of the Material Constitutive Models on the Adiabatic Shear Band Spacing：MTS，Power Law and Johnson－Cook Models［J］.International Journal of Solids and Structures，2004，41（11／12）：3109－3124.

［7］ 胡赓祥，蔡珣，戎咏华.材料科学与基础［M］.2版.上海：上海交通大学出版社，2006：188－193，212－213.

（Hu Gengxiang，Cai Xun，Rong Yonghua.Fundamentals of Materials Science［M］.2nd ed.Shanghai：Shanghai Jiaotong University Press，2006：188－193，212－213.）

［8］ 朱松鹤，戴兵，张恒华，等.F40级船板钢动态再结晶及流变应力研究［C］∥中国金属学会.第七届（2009）中国钢铁年会大会论文集.北京：冶金工业出版社，2009：235－239.

（Zhu Songhe，Dai Bing，Zhang Henghua，et al.Study on Dynamic Recrystallization and Modeling of Stress－strain Curves of F40Boat Plate Steel［C］∥The Chinese Society for Metals.The 7th（2009）CSM Annual Meeting Proceedings.Beijing：Metallurgical Industry Press，2009：235－239.）

［9］ 冀建平.45＃钢热粘塑性本构参数的确定及应用［J］.北京理工大学学报：自然科学版，2008，28（6）：471－474.

（Ji Jianping.Determination of the Thermo－viscoplastic Constitutive Relations of 45＃Steel［J］.Journal of Beijing Institute of Technology：Natural Science，2008，28（6）：471－474.）

［10］ Hou Qingyu，Wang Jingtao.A Modified Johnson－Cook Constitutive Model for Mg－Gd－Y Alloy Extended to a Wide Range of Temperatures ［J］. Computational Materials Science，2010，50（1）：147－152.