一种基于互信息的图像配准算法
郭 佳,李 辉,王 成,李思众
(西安应用光学研究所,西安710065)
随着传感器技术的迅猛发展,图像融合技术作为多传感器信息融合的一个非常重要的分支——可视信息的融合,近二十年来,引起了世界范围内的广泛关注和研究热潮[1-2]。图像配准是图像融合技术的基本环节和首要问题,它是对取自不同时间、不同传感器或不同视角的同一景物的两幅图像或多幅图像进行匹配、叠加的过程,只有经过配准后的图像才能进行有效的融合[3-6]。
在多传感器数据融合中,两种常见的传感器是红外和可见光传感器。研究高效准确的红外与可见光图像配准方法具有广阔的应用前景,特别是在军事领域中,可以获得更加全面的精确可靠的目标信息,提升对目标的精确打击以及全天候作战的能力。
传统的图像配准方法一般是采用选取控制点的方法,该方法在相同传感器下是可行的,但在多传感器图像配准时出现了一定的困难。这是由于多传感器图像反映的是物体不同的物理特性:其中一幅传感器图像中出现的特征在另一种传感器图像中未必会出现,如在红外图像出现的热油箱未必在可见光图像中出现。另一方面,选取控制点需要人工的干预,难以实现自动配准,费时费力。此外,由于红外与可见光处于不同波段,图像间的相关性较小,所以红外与可见光图像的配准相对来说,难度更大。目前,国内外有关红外与可见光图像的配准尚无成熟的算法。本文针对红外与可见光的图像特性,采用互信息作为两幅图像的统计相关性测度,并使用仿射模型实现两者的配准,得到了较好的效果。
1 互信息理论
互信息(Mutual Information)[7-8]是信息论中的一个基本概念,是两个随机变量统计相关性的测度。原理上,当两幅基于共同物理结构的图像达到最佳配准时,他们对应像素的灰度互信息应为最大,由于该测度不需要对不同成像模式下图像灰度间的关系作任何假设,也不需要对图像进行分割或任何预处理,因此,该测度可以被广泛的应用于多模图像配准。
熵[9]是互信息理论中的一个重要概念,它是用来测量一个信源所含信息量的测度。假设一个信源A输出N个消息,其中有n个不同的消息,第i个消息(i=1,2,…,n)重复 hi次,则 hi/N 为每个输出消息的重复频率,故可以用概率替换,即pi=hi/N。则该信源的平均信息量(熵)为:
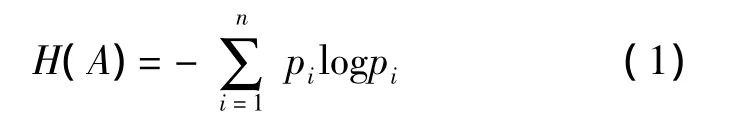
熵表达的是一个系统的复杂性或不确定性。对灰度图像来说,可以将图像的灰度看作是一个随机变量,图像中每个点的灰度取值为该随机变量的一个事件,则可以根据图像的灰度信息计算出每级灰度发生的概率pi=hi/N,其中hi为图像中灰度值为i的像素点的总数,N为图像中的像素总和。如果图像中的灰度级越多,像素灰度值分布越分散,则每级灰度的概率值很接近,或者说图像中任一点灰度值具有很大的不确定性,我们所获得信息量也就越大,该图像的熵值也较大。反之,如果图像中的灰度值比较集中,则一些灰度级的概念值也较大,不确定性减少,熵值较小。
联合熵H(A,B)是检测随机变量A和B相关性的统计量。对于两个随机变量A和B,它们的概率分布分别为pA(i)和pB(j),联合概率分布为pAB(i,j),则它们的联合熵H(A,B)为:
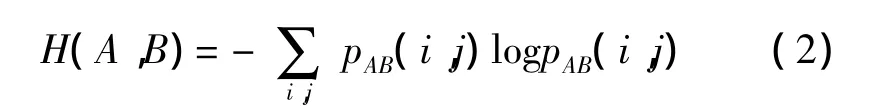
如果H(A,B)=H(A)+H(B),则A和B是相互独立的。反之,可用两个变量的联合分布与完全独立时的概率分布的广义距离来作为变量之间的相似性测度,即互信息:

互信息是用来度量A、B两个信源之间的依赖程度。对于待配准的两幅多传感器图像,可以认为它们是关于图像灰度的两个随机变量集A和B,并且它们存在较强的依赖关系。i和j分别为两幅图像中的对应部分的像素灰度值,i、j通过坐标变换T相联系,则两幅图像的互信息I(A,B)为:
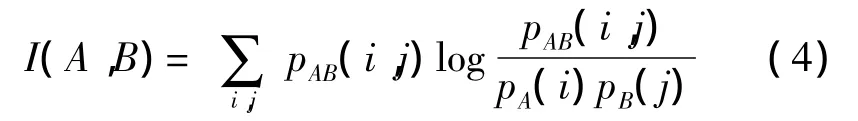
其中pA(i)、pB(j)和pAB(i,j)分别为两幅图像灰度的边缘概率分布和它们的联合概率分布。
由式(3)、式(4)可以看出,当图像对准时,A、B相互包含的信息总量应为最大。式(4)实际上是测量两幅图像灰度的联合概率分布 pAB(i,j)和当pA(i)与pB(j)独立时的联合概率分布pA(i)pB(j)之间的距离,它是两幅图像灰度相关性的一个测度。当采用(4)定义互信息时,互信息法配准图像基于如下假设,当两幅图像对准时,两幅图像之间的灰度相关性应为最大;当误配准发生时,该测度值会降低。
2 仿射变换
仿射变换[10-16]定义为:若变换 C:Rn→ Rn,C(X)=T(X)+a,T 是非奇异线性变换,a∈Rn,则变换C称为仿射变换。
仿射变换是一种线性变换,即具有平行线变换成平行线,有限点映射到有限点的一般特性,它可以描述3D空间中的目标到2D平面的成像过程。具体表现可以是各个方向尺度变换系数一致的均匀尺度变换或变换系数不一致的非均匀尺度变换及剪切变换等。它具有平移、旋转、和缩放不变性。仿射变换一般应用于场景图的配准,或者是简单/复杂背景中扩展目标的配准。
本文使用的仿射变换模型可以表示为:
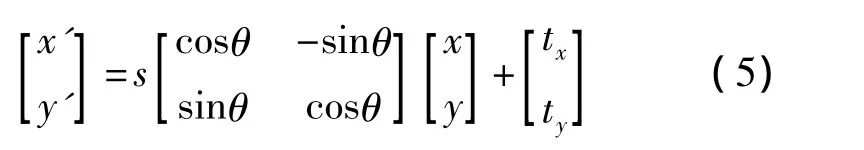
其中,(x,y)和(x',y')分别是两幅图像中对应点的坐标,s为尺度缩放因子,θ为旋转角度,tx,ty为平移量,这三者为图像配准的配准参数。
3 实验结果与分析
本文选取分辨率均为180×240的红外和可见光图像,对基于图像互信息的配准方法进行了仿真,实验结果如图1和图2所示,并给出了实验相关数据,如表1所示。从图1和表1中的实验数据中可以看出,图1中两幅图像(b)和(c)间有明显的尺度、旋转和平移变化,并且,由图2可以看出,图1中两幅图像(a)和(b)之间的尺度、旋转和平移等差别得到了很好的修正。实验结果表明,采用互信息作为红外和可见光图像的统计相关性测度,运用仿射变换模型进行成像差异较大的红外与可见光图像间的配准,效果较为理想,具有较高的实用价值。
4 结论
本文针对红外与可见光图像的特性及其配准的特殊性,提出了一种基于互信息的图像配准算法,并进行了算法仿真。实验结果表明,此算法是有效的,能够较好的进行图像间尺度、旋转和平移差别的修正,可以很好地解决成像差异较大的红外与可见光图像间的配准问题。

图1 红外与可见光图像基于图像互信息的配准结果

表1 红外与可见光图像基于图像互信息配准的相关实验数据

图2 配准后的图像
[1] 王利平,刘滨,陈钱,等.多传感器目标识别的图像数据融合技术研究[J].光电子技术,1998,18(9):239-242.
[2] 佘二永.多源图像融合方法研究[D].湖南:国防科学技术大学,2005.
[3] 廖惜春,丘敏,麦汉荣.基于参数估计的多传感器数据融合算法研究[J].传感技术学报,2007,20(1):193-197.
[4] 赵杰,江晶,盖旭刚.多无源传感器的在线配准[J].传感技术学报,2007,20(8):1894-1898.
[5] 倪国强,刘琼.多源图像配准技术分析与展望[J].光电工程,2004,31(9):1-6.
[6] 陶冰洁,王敬儒,张启衡.采用仿射变换的红外与可见光图像配准方法[J].光电工程,2004,31(11):39-41.
[7] 江静,张雪松,兰西柱.红外与可见光图像互信息法自动配准算法研究[J].华北科技学院学报,2006,3(4):73-78.
[8] 高鹏.基于边缘和互信息法的红外图像配准[J].红外,2013,34(1):30-36.
[9] 黄杰贤,杨冬涛,龚昌来.互信息熵与区域特征结合的图像匹配研究[J].激光与红外,2013,43(1):98-103.
[10]曾文锋,李树山,王江安.基于仿射变换模型的图像配准中的平移、旋转和缩放[J].红外与激光工程,2001,30(1):18-20.
[11]王金辉,陈冰,王建庄.实时图像仿射变换系统的研究与实现[J].自动控制与检测,2012(2):59-62.
[12] Mehfuza Holia,Thakar V K.Image Registration for Recovering Affine Transformation Using Nelder Mead Simplex Method for Optimization[J].International Journal of Image Processing(IJIP),2009,3(5):218-228.
[13]胡津翔,陈祺,王宏强.基于仿射变换的双波段红外图像配准算法研究[J].科技广场,2011,(1):103-106.
[14]张斌,周杨,陈书文,等.基于遗传算法与仿射变换的遥感图像配准[J].科学技术与工程,2010,10(21):5168-5170.
[15] Noppadol Chumchob,Ke Chen.A Robust Affine Image Registration Methood[J].International Journal of Numerical Analysis and Modeling,2008,6(2):311-334.
[16] Tanner C,Carter T,Hawkes D J,et al.Cylindrical Affine Transformation Model for Image Registration[J].Proc SPIE Medical Imaging:Image Processing,2010,7623(2):1-6.

