基于分离参数标定的鱼眼镜头成像模型研究*
朱均超,葛 磊,韩芳芳,刘 娜,张宝峰
(天津理工大学天津市复杂系统控制理论及应用重点实验室,天津300384)
随着计算机视觉的不断发展,常规镜头因为视场角的有限,在许多应用领域受到了限制;而鱼眼镜头是一种短焦距镜头,可以获得超大的视场角,可达到185度甚至270度的视场角[1],因而在在全方位视觉、机器人导航、虚拟现实及视觉监控等领域中有着重要的实用意义[2]。但鱼眼镜头应用的难点在于,鱼眼镜头的成像原理与普通光学镜有很大区别,成像规律不满足针孔成像模型,常规镜头射线投影定理并不适用[3]。且鱼眼镜头实现大场景范围的图像采集时,图像将带有较严重畸变,如图1所示。因此,本文对鱼眼镜头的成像模型进行研究,探索鱼眼镜头成像规律及标定方法,以便更好地将鱼眼镜头应用于其他方面[4]。

图1 鱼眼镜头及鱼眼图像
目前,国内外学者已提出了一些鱼眼镜头成像模型。英向华等[5]提出了球面透视投影模型;徐刚强等[6]提出了基于抛物面的投影成像模型;张琨等[2]通过分割圆的方法进行球面经度定位来模拟鱼眼镜头成像模型。本文采用物理参数分离标定的方法对鱼眼镜头成像模型的关键参数进行标定,进而提出基于分离参数标定的成像模型,可以得到鱼眼像素点与真实场景中物点的对应关系,计算更为简便,实时性高。
1 鱼眼镜头成像模型
鱼眼镜头成像,即将三维空间内一点经坐标变换,投影到二维成像面上的过程[7]。本文提出的鱼眼镜头成像模型如图2所示。
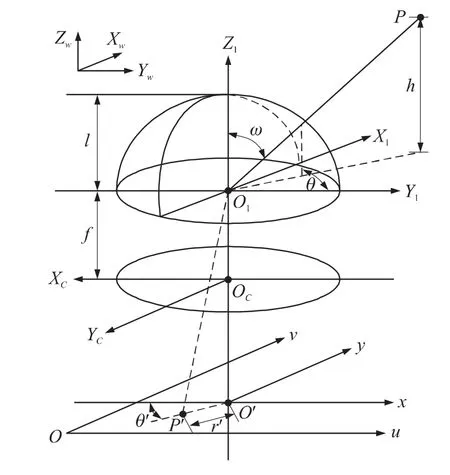
图2 鱼眼成像模型
其中包含五个坐标系:世界坐标系(Xw,Yw,Zw)、鱼眼镜头坐标系(Xl,Yl,Zl)、摄像机坐标系(Xc,Yc,Zc),图像坐标系(x,y)和成像面坐标系(u,v)。世界坐标系中任一点P在鱼眼镜头坐标系下的入射角为ω,该点在镜头坐标系的投影的偏移角为θ。成像面坐标系为图像坐标系的平移,图像坐标系的原心O'在成像面坐标系下坐标为(u0,v0)。在图像坐标系中,光轴的投影为原心O',点P的投影为P',O'P'的径向长度为r',与O'y轴负方向夹角为θ'。因此,根据图像坐标系下成像点 P'对应的r'、θ'值,拟合得到鱼眼镜头坐标系下入射光线OlP,记为 OlP(ω,θ)。
目前,绝大多数鱼眼镜头均基于四种成像模型制造,即“体视投影”,“等距投影”,“等立体角投影”[8]和“正交投影”[9]。本文基于等距投影模型展开讨论,如图3所示,“等距投影”表示视场角ω相等的物点在像面上具有等径向距离r',r'与视场角ω成正比,径向放大率不变,如式(1)。

但在实际成像过程中,k值在不同投影位置并不是恒定不变的,会存在径向畸变和切向畸变[10],畸变与像平面上径向距离 r'、切向偏移角 θ'有关[11]。本文的目的是设计分离参数标定实验,探讨鱼眼图像不同r'、θ'对应的像点与真实物点位置之间的关系,为后续的图像畸变校正研究提供模型参数。提出鱼眼图像像点与物点对应关系公式为:
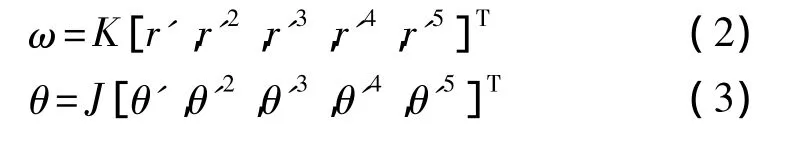
其中,K、J分别为径向畸变系数矩阵和切向畸变系数矩阵。

图3 等距投影模型
2 分离参数标定思想
2.1 标定思想及标定步骤
基于等距成像模型,径向距离r'可在鱼眼图像中直接测量,ω通过式(4)计算得到,从而可以根据式(2)对畸变系数矩阵K进行拟合。但虚拟成像距离l未知,因此,本文需要对虚拟成像距离进行标定。
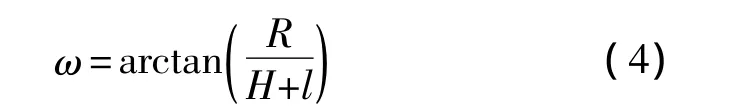
由于鱼眼镜头存在光学偏差以及镜头装配误差,造成图像中心偏离成像芯片靶面中心,因此首先确定图像中心坐标[12]。在标定图像中心及虚拟成像距离的基础上,研究畸变系数与r'、θ'之间的关系。考虑到径向、切向畸变的影响,设计新靶标对畸变系数进行标定。设计靶标由6组等距同心圆c1…6及10条过圆心且偏移角不等的射线L1…10组成,如图4所示。
让鱼眼镜头光心对准图4靶标中心O成像,光学系统光轴垂直于靶标平面。可以看出,靶标上每个同心圆上的点对于鱼眼成像系统具有相同的ω值,每条射线上的点具有相同的θ值,进而得到鱼眼镜头成像畸变系数与r'、θ'之间的关系。
具体标定步骤为:最小二乘法进行圆拟合,标定光学中心;根据成像系统几何关系,计算得到虚拟成像距离l;采集靶标图像,提取不同位置上的物、像点对,对畸变系数与r'、θ'之间的关系进行讨论。
2.2 光学中心及虚拟成像距离l标定
由于制造、装配误差等因素存在,物理镜头的光学中心与鱼眼图像的中心点存在一定偏差,而在实际标定中,首先要使鱼眼图像中心与物理靶标中心对准。因此,首先对鱼眼图像中心进行标定,为其他参数标定奠定基础。本文采用对图像边缘进行最小二乘法拟合圆曲线方法进行中心标定,圆心即为鱼眼图像中心,并获得鱼眼图像圆半径。
l为鱼眼镜头的虚拟成像距离,是标定畸变矩阵的前提,但l不能直接测量得到,因此,利用几何关系推导得到l的值。l的标定模型如图3,设P1、P2为OlP上任意两点,在成像面上投影均为点P'。P1A⊥O'Ol于 A点,P2B⊥O'Ol于 B点,则有 ΔOlAP1~ΔOlBP2,根据相似三角形几何关系,得到式(5)。
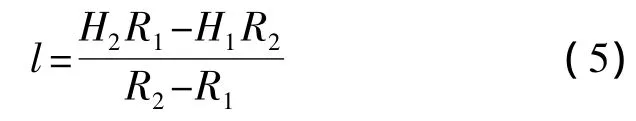
2.3 畸变系数的标定
上文已介绍,物点的入射角与成像面上投影点到光心的距离关系如式(2)所示,K为五阶径向畸变系数矩阵,展开得到式(6)。其中,r'为成像面上投影点到光心的径向距离,如式(7),(u,v)为成像面上的投影点,(u0,v0)为标定的光心坐标,ω在图像采集过程中,通过式(4)计算得到,R为靶标同心圆半径。
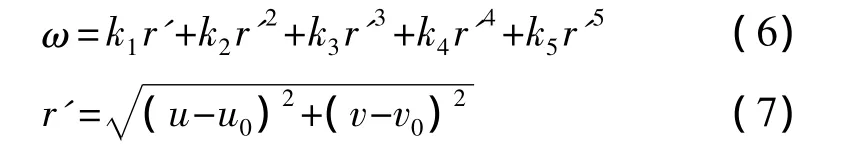
切向上的偏移角度可由式(3)进行拟合,展开可得到式(8)。其中,θ'可由式(9)得到。由于图像平面极坐标的周期性[5],当 θ'=2π 时,有 θ=2π,因此j5不是独立参数,可表示如式(10)。

其中,r'、θ'可通过鱼眼图像的像素点通过式(7)、式(9)计算得到,由r'值可知ω值,θ值在靶标中已设定。因此,可拟合得到畸变系数K和J,根据本文的投影模型,如式(2,3),可计算鱼眼图像的任一像点对应的空间内的物点位置。
3 分离参数标定实验分析
3.1 光学中心标定过程及结果
采集鱼眼图像,取灰度阈值为100(总灰度范围在0~255),将鱼眼成像圆形区域设为白色;利用canny算子对整个图像进行边缘检测,提取边缘轮廓;随机选取边缘上三个点,进行圆拟合[13],得到圆心坐标及半径,多次测量求平均值。
实验结果如图5所示,光心及半径拟合结果如表1所示。本文中图表均以pixel表示像素单位。

图5 获得光心坐标及半径的结果

表1 光心及半径实验数据及拟合结果(单位:pixel)
对上表所示的多次实验结果求平均,本文实验以(980,771)为光心坐标,鱼眼图像半径为767。
3.2 虚拟成像距离l的标定过程及结果
在鱼眼镜头采集程序中,标记图像中心(u0,v0),以及水平方向和垂直方向上(u0-300,v0)、(u0+300,v0)、(u0,v0-300)和(u0,v0+300)四个位置,如图6;移动改变靶标到鱼眼镜头平面的距离H,使得靶标中心与光心重合,标记的四个点与半径为R的同心圆 ci(i=1…6)重合,如图7,记下多组 H、R 值;由式(5)记算多组l值,实验数据如表2所示,求平均值。

图6 鱼眼图像标记设定

图7 移动靶标采集图像
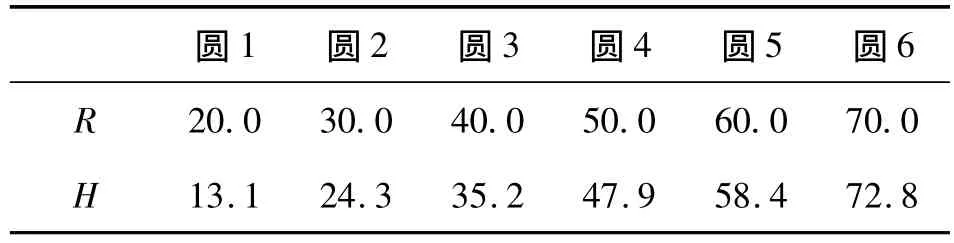
表2 实验数据(单位:mm,r'=300 pixel)
根据式(5)计算多组数据,求得l的平均值为12.410 7 mm。
3.3 畸变系数的标定过程及结果
具体实验步骤如下:
步骤1:采集靶标图像,使靶标中心始终与光轴中心重合,靶标横纵轴始终与标记点重合;
步骤2:沿光轴方向移动靶标,改变靶标到鱼眼镜头平面的距离H,记录同一射线与多组同心圆交点对应的H、R值,如图4中Ai(i=1…6);
步骤3:根据式(4)(7),由每组H、R值计算得到不同r'值对应的ω值;
步骤4:根据多组ω、r'值拟合得到径向畸变系数矩阵K,拟合数据如表3所示;
步骤5:固定标记点半径r'为300像素点,取同一鱼眼图像上多组不同射线与R=30.0 mm的圆的交点(u,v),如图4中Bi(i=1…10),由式(9)得到对应的 θ'值;
步骤6:θ值由靶标确定,根据每条射线的θ、θ'值拟合得到径向畸变系数矩阵J,拟合数据如表4;
步骤7:由式(2)、式(3)得到鱼眼镜头成像模型,取任意不同的靶标点,对比成像模型得到像素点与真实成像点的误差。

表3 标定K矩阵实验数据(θ=0)

表4 标定J矩阵实验数据(r'=300 pixelR=30.0 mm)
K 值拟合结果为 K=[19.749 1 36.906 2 25.624 8 -7.007 5 2.387 1]。误差值如图 8 所示,角度误差范围在±0.01内。
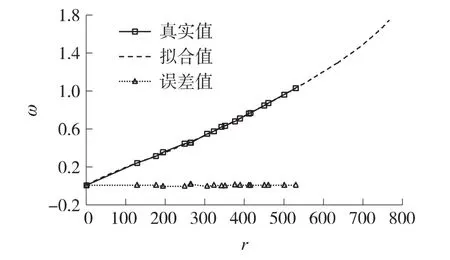
图8 径向畸变系数拟合结果(弧度/径向距离)
J值拟合结果如图9所示,将2π角展开,可看出误差轨迹在每一个象限内的规律基本相同,因此直接将角度在π/2,即单个象限内展开,如图10所示。J值的最终拟合结果为,J=[0.039 7-0.281 4 0.233 3 -0.040 4 -0.000 1]。如图11所示,角度误差可控制在±0.03内。

图9 切向畸变全角度展开(弧度/样本点)
3.4 成像模型误差分析
设计靶标如图12所示,取多组角点,通过式(6)、式(8)可以得到真实位置,记为(ω0,θ0);经鱼眼图像的成像点(r',θ'),根据本文提出的投影模型,如式(2,3),结果对比如表5所示。
可以看出,拟合得到的物点与真实物点存在极小的差值,其中ω参数和θ参数各自的误差值平均值分别为0.0115和0.0194,最大误差值分别控制在0.04 和0.03 内,如图13、图14 所示。

图10 切向畸变单象限展开(弧度/样本点)
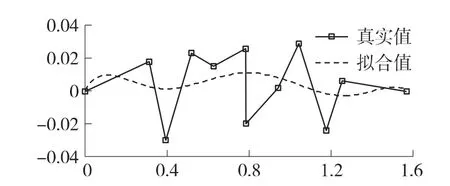
图11 切向畸变系数拟合结果(弧度差值/全角度)
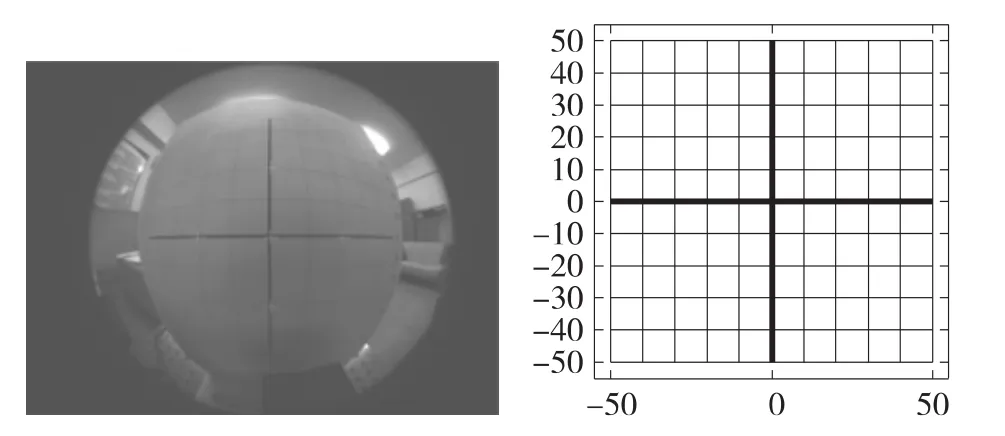
图12 误差计算靶标及鱼眼图像
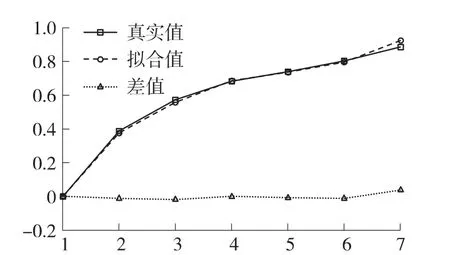
图13 ω参数误差分析(弧度/样本点)
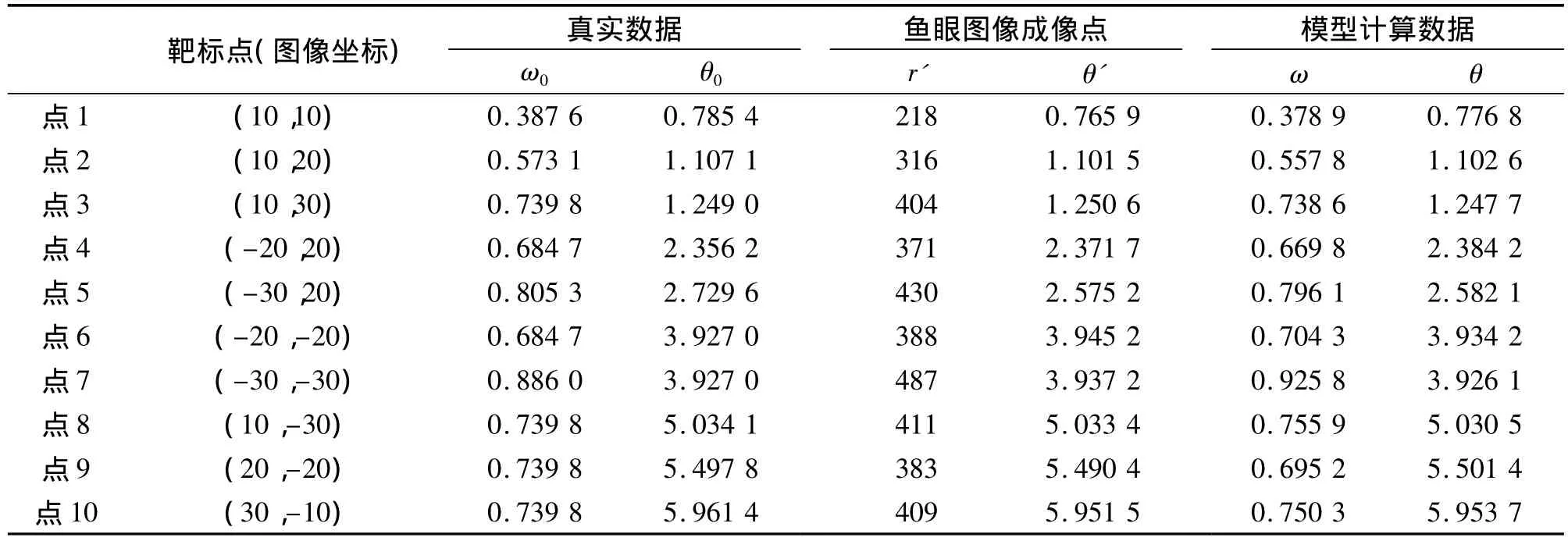
表5 投影模型与真实点的对比(H=40 mm)
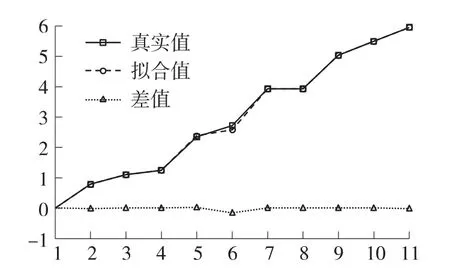
图14 θ参数误差分析(弧度/样本点)
4 结论
本文提出了一种通过对分离的物理参数进行标定的方法,探索研究鱼眼镜头的成像模型,得到鱼眼镜头成像模型公式,并拟合得到公式中的径向畸变系数矩阵及切向畸变系数矩阵。通过将经成像模型反推得到的物点与真实物点进行对比,可以看出误差很小,成像模型可以较好的模拟出鱼眼镜头成像过程。根据本文提出的成像模型,可以更好地进行鱼眼图像畸变校正、匹配[14-15]以及三维重建等后续工作。
[1] 王永仲.鱼眼镜头光学[M].北京:科学出版社,2006.
[2] 张琨,王翠荣.基于圆分割的鱼眼镜头图像畸变校正算法[J].东北大学学报,2011,32(9):1240-1243.
[3] 王迅.基于鱼眼相机的立体图像校正和图像拼接[D].浙江:浙江大学,2011.
[4] Moreau Julien,Ambellouis Sébastien,Ruiche Yassine.3D Reconstruction of Urban Environments Based on Fisheye Stereovision[J].8th International Conference on Signal Image Technology and Internet Based Systems,SITIS 2012:36-41.
[5] 英向华,胡占义.一种基于球面透视投影约束的鱼眼镜头矫正方法[J].计算机学报,2003,26(12):1702-1707.
[6] 徐刚强,郑利平.基于一种椭圆鱼眼图像的畸变校正模型[J].计算机技术与应用进展(CACIS·2010),2010:271-274.
[7] Ryberg A,Lennartson B,Christiansson A K,et al.Analysis and E-valuation of a General Camera Model[J].Computer Vision and Image Understanding,2011,115(11):1503-1515.
[8] Kanatani Kenichi.Calibration of Ulatra-Wide Fisheye Lens Cameras by Eigenvalue Minimization[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(4):813-822.
[9] Schneider D,Schwalbe E,Maas H.Validation of Geometric Models for Fisheye Lenses[J].ISPRS Journal of Photogrammetry and Remote Sensing,2009,64:259-266.
[10]贾云得,吕宏静,徐岸,等.一种鱼眼镜头成像立体视觉系统的标定方法[J].计算机学报,2000,23(11):1215-1219.
[11]吴方,王震.鱼眼镜头图像变形矫正算法研究[J].计算机科学,2009,36(4B):109-111.
[12] Huang Fuyu,Wang Yongzhong,Shen Xueju,et al.Method for Calibrating the Fisheye Distortion Center[J].Applied Optics,2012,51(34):8169-8176.
[13] 唐俊.鱼眼图像轮廓提取算法研究[J].微机发展,2004,14(10):10-12.
[14]邓传斌,郭雷,李维.基于SIFT的遥感图像配准方法[J].传感技术学报,2009,22(12):1742-1747.
[15]管业鹏,顾伟康.基于双目视觉的基准差梯度立体匹配法[J].传感技术学报,2004,3(1):74-77.

