超声多次回波反射法测量硅油粘度实验研究

翟灵慧，苏明旭，蔡小舒，吉肖

(上海理工大学颗粒与两相流测量研究所，上海200093)

粘度作为流体热物性数据的重要参数之一，在许多工业部门和科学研究领域中都具有重要意义，特别是在石油化工、医药、粘合剂、食品等行业，粘度的准确测量可有效地控制生产过程及产品品质［1－3］。在高性能流量计中，通过检测液体的粘度和密度求得液体的雷诺数后进行相关补偿，以获得更准确的流量计量。

传统的粘度测量有毛细管法、旋转法及振动法等，但是这些方法往往都要与被测介质直接接触，测量周期长，需要采样等，不太适合在线测量［4］。超声测量粘度由于具有非接触，测量周期短，无需采样等特点，适合在线测量。Mason［5］首先使用超声横波多次反射法来测量液体在不同频率下的粘弹性。粘弹性与液体的粘度和使用的超声横波频率有关。弹性能让横波在液体中传播，但也只能传播极小的距离，一般就几个微米［6］。因为有着非常高的粘性损失，所以直接测量液体中横波的传播特征量是不可能的［7］。本文从横波复反射系数出发，推导出在考虑液体弹性和不考虑液体弹性两种模型下的粘度计算公式，采用超声多次回波反射法对硅油粘度进行了测量，分析其随温度变化的关系。

1 测量原理

平面剪切波入射至匹配层与液体界面时，由于匹配层和液体剪切阻抗的差异，会导致横波的反射。反射系数表示反射波能量与入射波总能量的比值，其复数形式可写为:

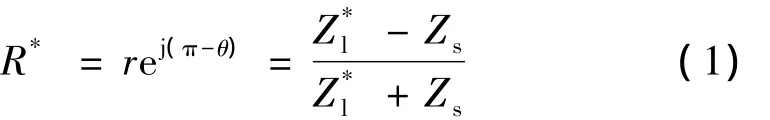
式中，r和θ分别为复反射系数R*的幅值和相位，j=为虚数单位，与Zs分别是待测液体和匹配层(固体)的剪切阻抗，由于声波在固体中的衰减与液体中相比非常小，可以认为固体的声阻抗为实数，即Zs=ρsCs，ρs与Cs分别是固体的密度和固体中的横波传播速度。液体的声阻抗可以写作如下形式:

式中:Rl是声阻，Xl是声抗。已知粘弹性介质中一维波动方程为［8］:

波动方程 (3)的解为:μ(x，t)=μ0exp(jωt－Гx)，其中ω为剪切波的角频率，Г是复波数，液体中剪切阻抗和复剪切模量的关系如下［9］:

式中:ρl是液体粘度，G*称复剪切模量，定义为

式中:实部G'为弹性模量;虚部G″=ωη为粘性模量。

考虑超声横波从固体介质入射到液体，如图1所示，可以给出如下关系［10］:

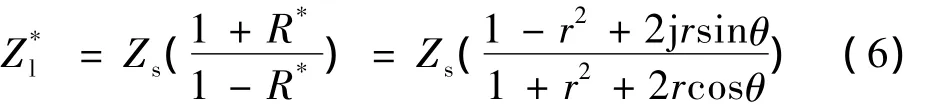
联立公式 (2)(4)(5)(6)，可得，

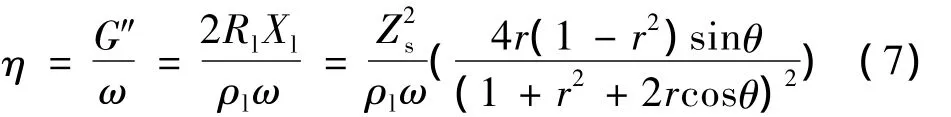
对于纯粘性液体 (即G'=0)，Rl=Xl，液体粘度公式为

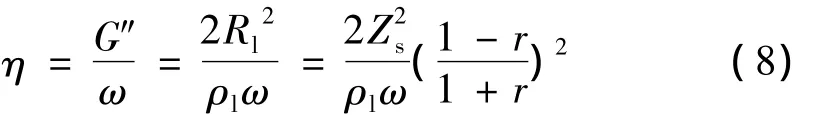
下文中将公式 (7)称为计算液体粘度的完整模型，而 (8)看作简化模型。通过测量液体密度、反射系数的幅值r与相位θ，即可由上述模型求得液体粘度值。

2 实验装置和方法

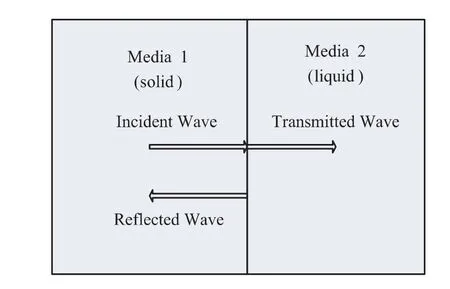
图1 横波在固液界面处垂直入射示意图

图2为实验装置图，测量装置主要包括PR-5800型超声脉冲发射接收仪，高速信号采集卡以及计算机数据处理系统。测量信号经过硬件滤波并放大后，由高速数据采集卡进行信号模数转换和采集，并送入计算机进行处理。实验使用传感器为美国Panametrics公司生产的V154-RB水浸超声横波换能器，其中心频率为2.25 MHz。另外，实验中还使用上海图新电子科技有限公司的EDS-300数显密度计测量液体密度，上海尼润智能科技有限公司生产的SNB-1型旋转式粘度计用于粘度值的对比测量，使用宁波新芝生物科技股份有限公司提供的DC-0520低温恒温槽调节温度变化，同时自行设计了外循环恒温测量装置，分别如图3中(a)，(b)，(c)，(d)所示。实验使用的固体匹配层为石英玻璃 (其剪切阻抗Zs=8.25×106kg·m－2·s－1)，并采用特殊的横波耦合剂。

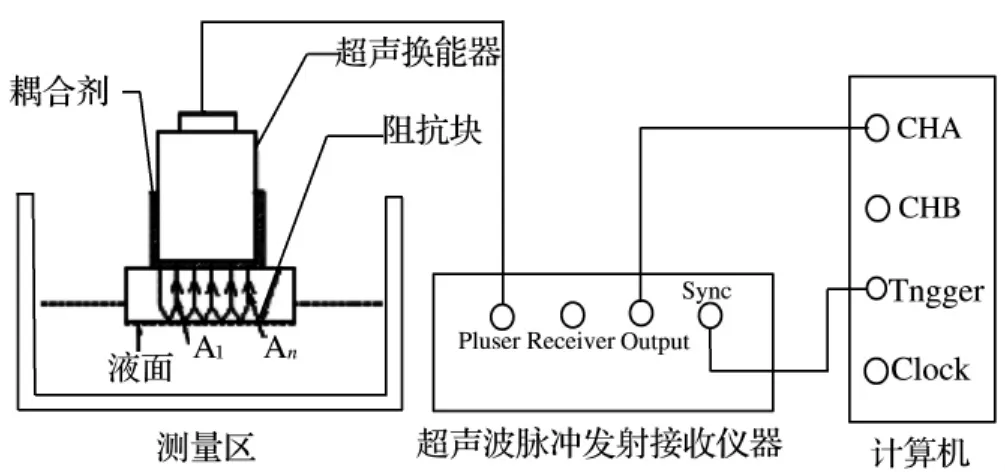
图2 实验系统示意图

3 实验数据与分析

以三种不同规格的国产硅油为样品，这里分别称为1号硅油，2号硅油和3号硅油。试验对3号硅油在20，25，30，40，50℃五个温度点时的横波信号以及3种硅油在25℃时的横波信号进行测量与分析。三种硅油样品25℃的粘度计粘度值和以及密度计所测密度值如表1所示。

图3 外循环恒温测量装置示意图

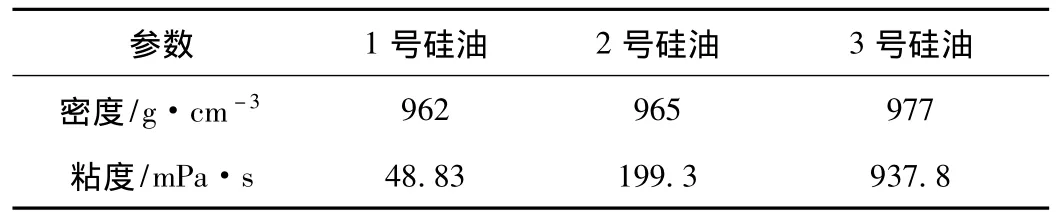
表1 25℃时三种硅油的粘度和密度值

图4给出了超声横波在石英玻璃/3号硅油界面的多次反射回波，可以清楚地看到6次回波，对每次回波作快速傅里叶变换 (FFT)，并获得频域上的幅值。

图4 多次反射回波信号

图5是对幅值取对数后与回波次数做线性拟合，可得到直线斜率k=0.524，反映了横波在界面上的反射和匹配层吸收导致的声能损失。图5中线性拟合的相关系数R2达到0.994，可见采用多次回波拟合的方法可以很好地抵消发射仪不稳定性和信号本身的随机误差影响。考虑第M个和第N个回波，有如下关系式［11］:

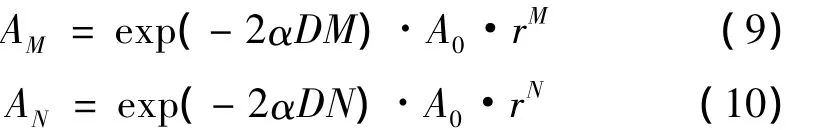
式中:A0为原始声压幅值;AN表示第N次回波幅值;α表示石英玻璃中的声吸收系数;D表示匹配层厚度;r表示石英玻璃与待测液体间的复反射系数幅值。

将上两式取对数并相减可得

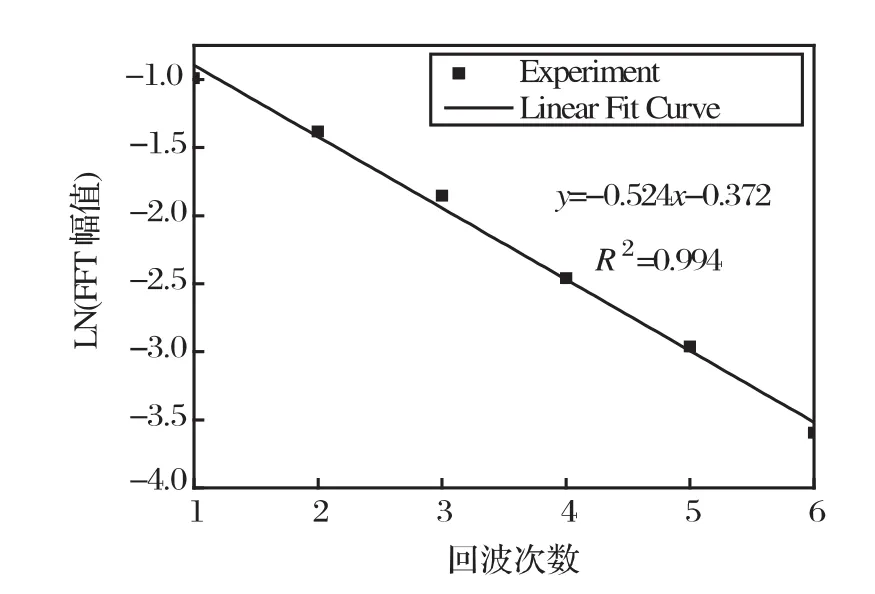
图5 回波次数与回波幅值对数值关系图

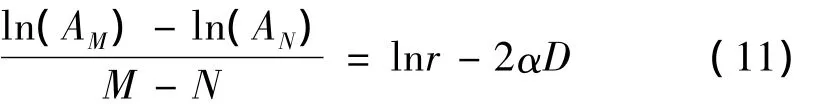
式 (11)中等号左边一项即为图5处理所得拟合斜率k。以空气作为参照物，可以得到

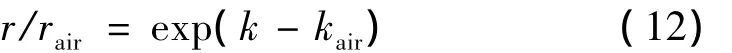
式中:下标air代表参照物空气。一般情况下，认为石英玻璃/空气界面是全反射，即rair=1，再根据样品斜率k、空气斜率kair，就可以确定待测样品的反射系数幅值r。

相位角θ可以通过公式 (3)来计算［12］，即

式中:ΔtN是液体中第N次回波与参照物空气中第N次回波的时间差。

图6、图7分别为3号硅油所测反射系数幅值与相位角随温度的变化曲线。从图中可见，超声横波换能器在石英玻璃/硅油界面发生反射后的反射系数幅值随温度升高，而相位角随温度降低。

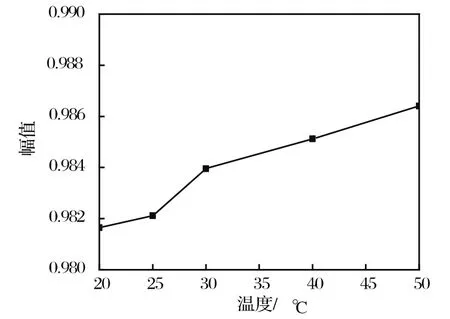
图6 幅值随温度变化曲线

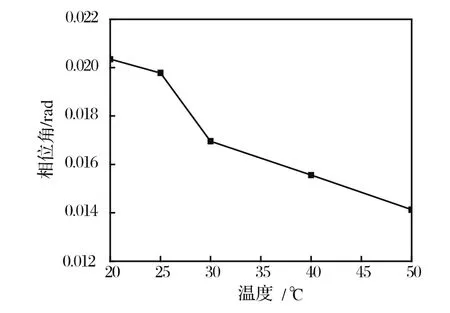
图7 相位角随温度变化曲线

图8为两种模型下测得的粘度值与旋转粘度计所测结果的对比。可以看出，超声法和SNB-1型旋转粘度计测得的粘度值都随温度的升高而降低，这与液体粘度随温度变化的特性相符合。由于高频率超声下硅油的弛豫现象，简化模型测得超声粘度值与考虑了相位角变化的完整模型结果有一定差别，随着温度增加样品粘度减小，同时弛豫效应减弱，二者差别也减小。超声法结果与旋转粘度计比较，趋势一致，但数值上存在一定偏差，对于完整模型该相对偏差小于20%。

图9为三种不同规格硅油样品在25℃时测量结果的对比，可以看出，三种不同规格的样品被很好地区分，完整模型测量值和简化模型测量值相比，与旋转粘度计更为接近，而且可以看出随着粘度本身的增大，不同模型和方法间的相对偏差减小。由于超声法和旋转粘度计在测量原理上的差异性，上述偏差可以理解，由于它们给出的温度变化趋势一致，表明经过标定，超声横波反射法可以准确地测出液体粘度值。又由于超声波测量的非接触特性，可以实现实时在线测量。

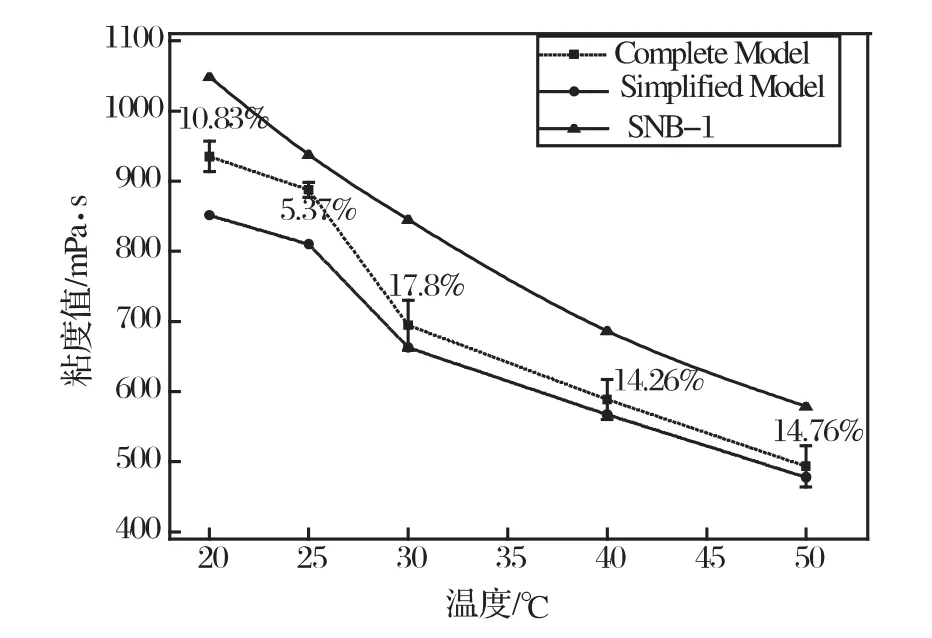
图8 简化模型、完整模型和SNB－1型粘度计结果对比

4 结论

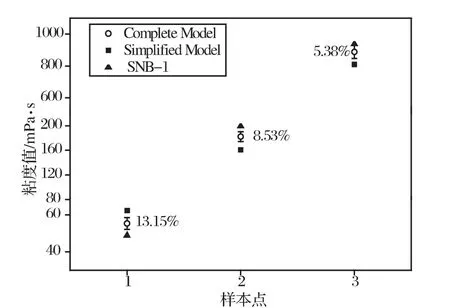
图9 三种硅油的粘度测量结果对比

用超声横波多次回波反射法测量了三种硅油的粘度值，通过未考虑液体弹性的简化模型和完整模型进行数据分析，获得粘度值随温度的变化曲线。结果表明，两种模型下所测得硅油粘度值均随温度的升高而减小，这符合液体粘度的温度变化特性。将两种模型测得硅油粘度数值与SNB－1型旋转粘度计相比，完整模型所测得的结果偏差更小，可在经过标定后实现在线测量。考虑到采用超声多次回波反射法还具有结构简单、非侵入式测量以及不受超声发射功率变化影响等特点，可实现化工过程中单一液体和混合液体粘度的实时监测。

［1］Giordano D，Ding well D B.Viscosity of Hydrous Entabasalt，Implication for Plinian-style Basaltic Erupitions［J］．Bulletin of Volcanology，2003，65(1):8－14.

［2］ Mario Minale，Pier Luca Maffettone.Morphology Estimation from Normal Stress Measurement for Dilute Immiscible Polymer Blends［J］．RheolActa，2003，42:158－165.

［3］ Feng-JuiKuo，Chung-Teh Sheng，Ching-Hua Ting.Evaluation of ultrasonic propagation to measure sugar content and viscosity of reconstituted orange juice［J］．Journal of Food Engineering，2008，86(1):84－90.

［4］杨璇.超声波多次回波反射法测量液体的密度和粘度［D］．上海:上海理工大学，2011.

［5］ Mason W.P，Baker W.O，Mcskimin J.M，et al.Measurement of shear elasticity and viscosity of liquids at ultrasonic frequencies［J］．Phy.Rev.，1949，75(6):936.

［6］ Greenwood M S，Bamberger J A.Measurement of viscosity and shear wave of velocity liquid or slurry for on-line process control［J］．Ultrasonic，2002，39(9):623－630.

［7］ Harrison G，Barlow A J.Dynamic viscosity measurement［J］．Methods in Experimental Physics，1981，19:137－178.

［8］ Franco E E，Adamowski J C，Buiochi F.Ultrasonic viscosity measurement using the shear－wave reflection coefficient with a novel signal processing technique［J］．IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2010，57(5):1133－1139.

［9］ Franco，EE，Adamowski，JC，Higuti，R T，et al.Viscosity measurement of Newtonian liquids using the complex reflection coefficient［J］．IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2008，55(10):2247 －2253.

［10］ Dixon S，Lanyon B.Phase change measurement of ultrasonic shear waves on reflection from a curing epoxy system［J］．Applied Physics，2005，38:4115－4125.

［11］薛明华.超声法颗粒两相介质多参数测量的理论及实验研究 ［D］．上海:上海理工大学，2010.

［12］ Lellinger D，Sulimma J，Tadjbakhsch S.Ultranosic shear wave reflection method for measurements of the vicoelastic properties of polymer films［J］．American Institute of Physics，1996，68(3):1536－1542.