深空探测返回器再入制导仿真分析*
深空探测返回器与近地轨道再入航天器相比具有再入速度大、最大过载大、临界点最大热流量大、再入走廊窄等特点,面对更加恶劣的再入环境和各种不确定性,如何保证深空探测返回器安全无损准确地返回到预定着陆区,这对再入制导和控制系统提出了更高的要求.
再入制导方法分为两类[1],一类是利用标准轨道的制导方法,称为标准轨道法;一类是利用预测能力对落点航程进行预测的制导方法,称为预测落点法.由于两种制导方法各有其优缺点,本文将分别采用LQR标准轨道制导法和预测制导法对深空探测返回器进行研究,分析每种方法对初始再入条件的适应性以及在各种情况下的落点精度,为中国正在进行的深空探测返回再入制导提供参考.
1 再入动力学
再入过程的三自由度质点动力学方程描述如下[2]:
(1)
(2)
(3)
cosθsinφsinξ)
(4)
(5)
(6)
式中,ω是地球自转角速度,r是飞行器的地心距,λ为经度,φ是纬度,v是飞行器的速度,θ是飞行路径角,ξ是速度方位角,ξ=0表示正东方向,σ为倾斜角,σ=0表示升力在当地铅垂面内.D和L分别表示气动阻力加速度和升力加速度,定义为:
(7)
(8)
式中,ρ(r)是大气密度,Sref是飞行器参考面积,m是飞行器质量,α是飞行器攻角,M是马赫数,CD是阻力系数,CL是升力系数.
2 LQR制导
LQR制导律的设计归结为对反馈增益系数的确定.对纵向运动方程沿着标准轨道线性化,然后利用线性最优调节器原理设计制导律.在每个制导周期内求解代数Riccati方程,利用其正定解构造反馈控制律,与标准轨道的控制量叠加形成全量控制,用于实际再入轨道的制导[3].
2.1 纵向制导
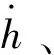
(9)
(10)
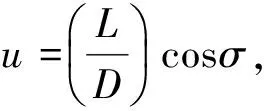
对非线性控制系统
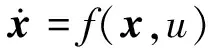
(11)
线性化,得到偏差模型
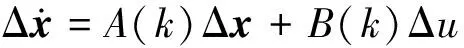
(12)
沿着标准轨道线性化获得A(k)和B(k),即
(13)
x*(k),u*(k)表示标准轨道对应的状态和控制输入.
对偏差模型式(13),假设从k时刻开始,系统参数A(k),B(k)保持不变,取性能指标为

(14)
式中Qk,Rk表示k时刻的加权矩阵,Qk>0,Rk>0.由此可得到k时刻的最优反馈控制律
(15)
式中Pk是如下代数Riccati方程的解:
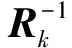
(16)
当(A(k),B(k))可镇定时,式(16)有唯一正定解Pk>0,并且此解是镇定解.
由此得到总的控制量为
u(k)=u*(k)+Δu(k)
(17)
u(k)作用于系统直到获得新的采样数据,再采用同样的方法计算新的控制输入.
2.2 侧向制导
侧向制导通过将侧向航程控制在某一范围内来实现,将侧向航程的误差边界设计成漏斗形,其形式如下[1]:
(18)
其中:
(19)
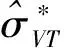
3 预测制导
按基准升力控制规律对返回器进行控制,理想情况下将使其飞到预定落点.由于实际飞行中的误差和扰动,实际落点和预定落点之间将产生纵程误差ΔR和横程误差ΔZ,为消除落点误差,需对基准升力控制规律进行修正.
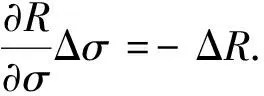
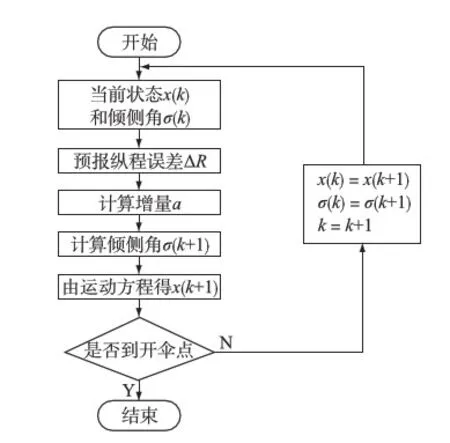
图1 预测制导流程图
4 仿真分析
取标准初始再入条件为:re=100km,ve=11049.5m/s,θe=-5.4°,在再入坐标系中对应的位置和速度分别为y=[0,6471004,0]Tm,v=[11000,-1040,-100]Tm/s.对应标准轨道的高度、速度、航程随时间变化曲线如图2所示.
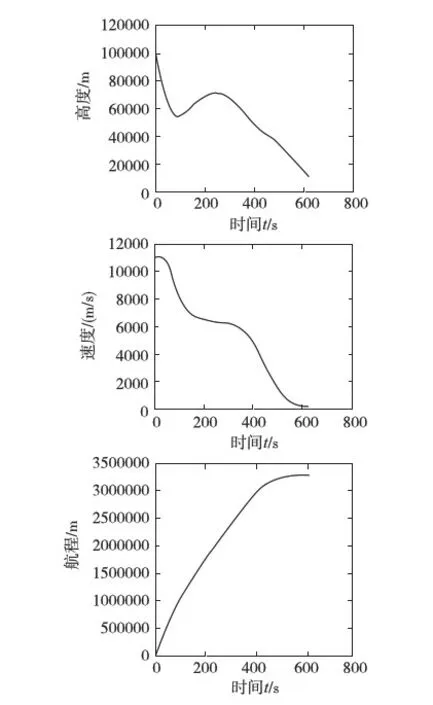
图2 标准轨道的高度、速度、航程随时间变化曲线
当初始再入位置和速度存在偏差时,对LQR和预测制导进行仿真,仿真结果如表1所示.

表1 LQR制导和预测制导误差比较

续表
5 结 论
本文针对以第二宇宙速度再入的返回器,分别采用LQR标准轨道制导法和预测制导法进行制导仿真分析.仿真结果表明,在较大的初始偏差情况下,预测制导律比LQR制导律具有更小的航程误差.
参 考 文 献
[1]赵汉元. 飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社, 1997
[2]王希季. 航天器进入与返回技术上册[M]. 北京:宇航出版社,1991
[3]杨俊春,倪茂林. 基于Riccati方程解的再入飞行器制导律设计[J]. 航天控制,2006,24(4):31-34
Yang J C, Ni M L. Design of guidance law for reentry vehicles based on the solution of Riccati equation[J]. Aerospace Control,2006,24(4):31-34
[4]胡军. 载人飞船全系数自适应再入升力控制[J].宇航学报, 1998, 19(1):8-12
Hu J.All coefficients adaptive reentry lifting control of manned spacecraft[J]. Journal of Astronautics, 1998, 19(1):8-12

