捷联式陀螺仪再平衡回路数字控制研究*

在工程应用中，目前捷联式陀螺仪大部分采用模拟式再平衡回路，然而导航计算机需要陀螺仪数字量数据，而陀螺仪模拟再平衡回路无法直接输出数字量，需要附加转换电路，可见模拟再平衡回路在直接数字输出方面已显现出劣势.现今电子技术和现代控制技术蓬勃发展，而模拟再平衡回路无法实现数字控制，对现代控制算法无法实现，制约了现代控制技术的在陀螺仪中的应用.基于以上两点，可以发现模拟式再平衡回路已制约了陀螺仪性能的提高.实际中，对高精度的陀螺仪的迫切需求，也要求对陀螺再平衡回路进行数字化研究.

在捷联系统中，陀螺必须工作于闭环状态，使陀螺仪输出轴上的力矩和为零.当陀螺的转子自转轴感受到外部角运动时，转子自转轴由于定轴性要在惯性空间保持固定方向，但是陀螺壳体随着外界角度变化要跟随转动，这时自转轴和陀螺壳体之间的夹角将发生变化.如果没有其他措施，夹角可能一直增大到使陀螺失去测量功能.为了使陀螺仪保持测量功能，必须在陀螺输出轴上施加力矩.当输出轴上控制力矩与外界输入角速度产生的力矩相互抵消时，陀螺自转轴就将保持在静止位置.这种由原来的静止平衡状态过渡到新的静止平衡状态的过程叫做再平衡，其力矩反馈回路叫做再平衡回路.再平衡回路有两大功能，一是控制功能，在转子轴感受外界角速度时再平衡回路将其拉回到新的平衡位置；二是测量功能，陀螺仪感受到外界角速度时会在回路中产生与该角速度成比例的电信号，测量这个电信号就可以知道外界输入角速度的量值.再平衡回路作为陀螺控制回路，要具有良好的动态和稳态性能，作为测量回路，又要有极高的线性度和稳定度，可见再平衡技术是发展捷联惯性系统的关键技术之一[1-2]，因此研究陀螺仪数字再平衡回路具有十分重要的意义.

1 再平衡回路

单自由度陀螺仪再平衡回路原理如图1所示.根据施加在陀螺仪力矩器上电信号的形式，可以将再平衡回路分为两大类，模拟再平衡回路和脉冲数字再平衡回路.

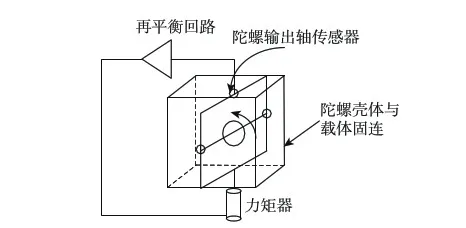
图1 陀螺再平衡回路示意图

模拟式再平衡回路如图 2所示，流经力矩电流发生器的是连续变化模拟量，加矩方式称为模拟加矩.为精确地测量力矩器电流，同时又便于与数字计算机配合，一般采用精密电阻对电流信号进行采样，再用V/F或A/D转换电路将其变为数字信号[1].

脉冲式再平衡回路如图3所示，流经力矩电流发生器的信号是幅值恒定，时间连续，信号可以在电流方向和持续时间上调制的脉冲量，加矩方式称为脉冲加矩.测量信号经过简单的处理可以直接送入计算机，不需要转换电路.

随着电子技术的发展，特别是FPGA(fleld programmable gate array)和DSP(digital signal processor)技术的兴起，现在又产生一种全新的设计思想，即全数字式再平衡回路.如图 4所示，它将回路中的大部分电路集中于数字处理芯片中，直接实现脉冲加矩和数字输出.

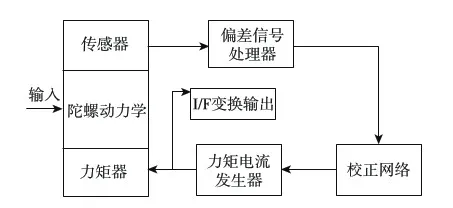
图2 模拟式再平衡回路

图3 脉冲式再平衡回路

图4 全数字式再平衡回路

模拟式再平衡回路以其设计简单、技术成熟等优势被大范围使用.但是随着对陀螺应用的进一步需求，在实际中模拟式回路出现了应用瓶颈.全数字化再平衡回路虽然是革命性的，但是在实际应用中有待进一步验证.

本文提出一种折中的再平衡回路实现方式，主要思想是只将模拟式再平衡回路中的控制器数字化，集中于FPGA中，力矩器仍然采用模拟加矩方式，原理如图5所示.采用此种方案数字输出的问题可以得到解决，控制器也可以采用现代控制技术设计， 既继承已有的成熟技术，又有改进创新.

图5 新型再平衡回路

2 再平衡回路建模与控制

2.1 工作原理

当捷联于运载体的陀螺仪随载体转动时，陀螺仪输出轴上将产生一个与输入角速度分量成正比的陀螺力矩，该力矩使陀螺浮子产生角偏移，传感器把浮子的角偏移变成的载波信号，经放大、解调、滤波后，得到与浮子偏角成正比的电压信号，该信号经A/D转换后送入FPGA.力反馈控制算法根据角偏移产生控制量，经D/A转换和功率放大后给陀螺力矩器施加电流，其产生的电磁力矩正好与陀螺力矩相平衡，从而使浮子总是处于零位附近，如图6所示，FPGA输出到D/A的控制量就反映了输入角速度.

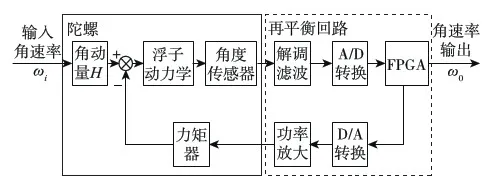
图6 工作原理图

2.2 建立模型

由2.1节可知，整个回路由误差处理电路、控制网络和力矩器组成.本文以单自由度液浮陀螺为对象设计再平衡回路，由文献[3]可知单自由度陀螺仪的角运动量β与外加力矩T之间的微分方程式为

(1)

其中，J为浮子转动惯量，C为阻尼系数，B为弹性约束力矩系数，β为浮子转角，T为加在浮子上的力矩.对于本文研究的液浮陀螺弹性约束力矩为系数零，因此式(1)在初始状态为零时的条件下拉氏变换后得到动力学传递函数为：

(2)

误差处理电路简化为比例环节K，控制器输出电压转电流系数为KVI.由于噪声的干扰，回路中还应加入低通滤波器，其传递函数为一阶惯性环节.力矩器可用一个简单的低通网络来表示[4]：

(3)

再平衡回路方框图如图 7所示，T为外加力矩，Tq为回路产生的平衡力矩，Gc(s)为控制器，Gf(s)为低通滤波模型.

图7 再平衡回路方框图

将图 7变换为控制原理方框图(图8)，uω为角速度输入产生的电压，uq为加矩到陀螺输出的电压，u0为控制器的输出电压，G(s)为等效被控对象[5].

G(s)=KKVIF(s)Gq(s)Gf(s)

(4)

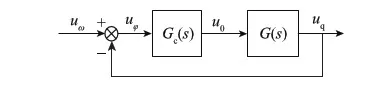
图8 控制原理方框图

2.3 控制器设计

文献[3]推导单自由度陀螺模型过程中，假设β为小量，对动力学方程进行线性化处理，忽略一些小参量，所以得到的模型不是十分准确.尽管陀螺采用确定的模型，其参数的确定也不是十分精确.基于这样的模型设计的控制器，得到的陀螺再平衡回路控制精度一定不会很高.本文采用的数字化再平衡回路中需要必须借助A/D转换电路，对模拟量进行数字化，但是由于A/D存在量化误差，其精度会在换转过程中损失一部分，利用原有模型设计控制器必然限制了陀螺仪精度的提高.

基于上述原因，本文采用吴宏鑫院士提出的基于特征模型的黄金分割自适应控制算法.特征建模形式简单，有利于控制器的设计.根据特征建模思想，将回路的研究对象简化为一个二阶系统[6]

(5)

其相应的差分方程为

y(k)=α1y(k-1)+α2y(k-2)+β0u(k-1)

(6)

其中，y(k)代表系统输出，u(k)代表输入控制量.

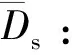
(7)

黄金分割控制器为：

(8)

y(k)=ΦΤ(k-1)θ(k)

(9)

其中

(10)

递推最小二乘算法：

(11)

已知某陀螺的模型和力矩器传递函数

(12)

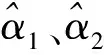
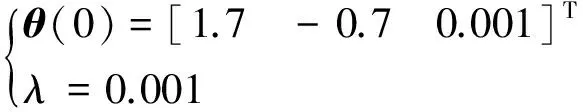
(13)

控制器设计的对象模型是特征模型，被控对象仍然是原系统模型，所以进行仿真时，被控对象采用原系统动力学模型.

2.4 仿真验证

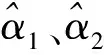
(1)采用12位A/D转换进行仿真

首先，对采用12位A/D转换的再平衡回路在黄金分割控制所用下的控制结果进行仿真.

(14)

陀螺随机漂移约为：0.2359(°)/h.

其次，对采用12位A/D转化的再平在抗积分饱和的PID控制算法作用的控制结果进行仿真.可得陀螺仪随机漂移为0.8524(°)/h.

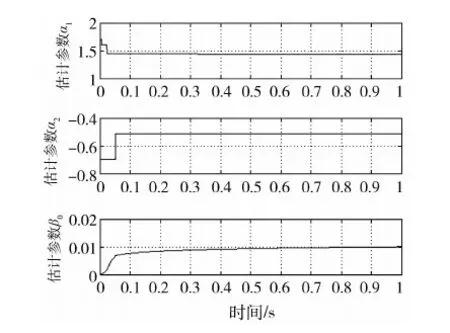
图9 12位A/D参数估计值

可以看到采用基于特征模型的黄金分割自适应控制算法相比与抗饱和的PID控制算法，陀螺仪的随机漂移明显减小.

(2)采用16位A/D转换进行仿真

首先，对采用16位A/D转换的再平衡回路在黄金分割控制所用下的控制结果进行仿真.

(15)

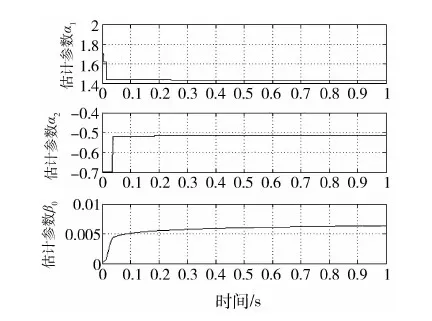
图10 参数估计值

系统带宽(tr为系统上升时间)：

(16)

随机漂移约为：0.0265(°)/h.

其次，对采用16位A/D转化的再平在抗积分饱和的PID控制算法作用的控制结果进行仿真.

通过参数迭代得到一组优化的PID参数.

(17)

随机漂移为：0.1534(°)/h.

可以看到采用基于特征模型的黄金分割自适应控制算法相比与抗饱和的PID控制算法，陀螺仪的随机漂移也明显减小.

(3)结果分析

根据上述结果可知，采用此方法相比于采用传统PID控制回路陀螺仪随机漂移显著减小.因为采用自适应黄金分割控制算法，将A/D量化误差引入参数估计迭代算法中，估计的参数融入了量化误差的信息，这是经典控制算法无法达到的.

通过与PID控制结果比较可以证明，采用基于特征模型的黄金分割自适应控制算法，确实降低了陀螺仪的随机偏移，提高了陀螺仪的性能.

3 结 论

本文提出的陀螺仪数字化再平衡回路，有效地解决了模拟再平衡回路在数字输出和应用现代控制技术方面的缺陷；针对数字化再平衡回路中普遍存在的模数转换过程中量化误差的问题，本文采用基于特征模型的黄金分割自适应控制算法，仿真表明采用此种控制方案能有效抑制抑制量化误差对系统性能的影响，使陀螺仪性能显著提高.

参 考 文 献

[1]张连超,范大鹏,范世珣．动力调谐陀螺再平衡回路技术的发展与研究现状[J]．导弹与航天技术，2008(1):36-40

Zhang L C, Fan D P, Fan S X. Developmentand current states of rebalance loop technology for dynamically tuned gyro[J]. Missile and Space Vehicle， 2008(1):36-40

[2]吴本寿,万德钧,周白令．国外动调陀螺再平衡回路技术的发展[J]．中国惯性技术学报,1998,4(2):52-57

Wu B S, Wan D J, Zhou B L. Development of rebalance loop for DTG in the world[J]. Journal of Chinese Inertial Technology, 1998,4(2):52-57

[3]郭秀中,于波,陈云相．陀螺仪理论及应用[M]．北京：航空工业出版社，1987

[4]Kennedy E J, Blalock T V, Bryan W L, et al. High-reslution width-modulation pulse rebalance electronics for strapdown gyroscope and accelerometer[R]. NASA-144086, 1974

[5]胡寿松．自动控制原理[M]．4版.北京：科学出版社，2001

[6]吴宏鑫,胡军,解永春．基于特征建模的智能自适应控制[M]．北京：中国科学技术出版社，2009

[7]薛定宇．控制系统计算机辅助设计[M]．2版.北京：清华大学出版社，2006

[8]郭素云．陀螺仪原理及应用[M]．哈尔滨：哈尔滨工业大学出版社，1985