带障碍的量子粒子群聚类算法

马 程， 郭有强

2001年,K.H.Tung[1]等首先提出带障碍的聚类问题COD(Clustering with Obstructed Distance)及COD-CLARANS[1]算法,为聚类的研究领域开辟了一个新的研究方向。自此之后,人们提出了多种比较典型的处理空间约束聚类算法,主要包括AUTOCLUST+[2],DBCLUC[3]和 DBRS+[4],每种算法各有特点。目前存在许多改进的障碍约束算法,有的是将新概念、新思想引入空间聚类挖掘中的创新算法,还有的融合了多种聚类方法的思想,如包括基于群体智能算法的聚类方法[5-6]、模糊聚类方法[7-8]、处理大规模数据的聚类方法等。本文采用群体智能算法中的量子粒子群算法解决障碍约束问题。

1 构造两点间的障碍距离

处理障碍约束主要有绕行路径(Detour Path)和绕行距离(Detour Distance)两种方法,本文采用绕行距离法作为处理障碍约束的方法。在使用绕行距离法处理障碍约束时,求解存在障碍物情况下两点间的最短距离是一个关键问题。

本文将需要求解的最短距离称为两点间的障碍距离(Obstructed Distance),记作为DO,定义如下:

定义1 直接可达距离二维平面上存在两点A、B以及障碍物集合O={O1,O2,O3,…,On},Oi表示第i个障碍物的封闭曲线(1≤i≤n),在点A与点B之间作一条连接线段LAB,若LAB与所有的障碍物封闭曲线Oi(1≤i≤n)均不相交,则定义LAB为A、B两点的直接可达距离,并且称A、B两点为相互可见点(VisiblePoint),记为VP(A,B)。

定义2 间接可达距离.二维平面上存在两点A、B以及障碍物集合O={O1,O2,O3,…,On},若存在一组点集合C={C1,C2,C3,…,Cm}使得{(A,C1),(C1,C2),(C2,C3),…,(Cm,B)}均为相互可见点,直接可达距离分别为{LAC1,LC1C2,LC2C3,…,LCmB},则以上直接可达距离之和定义为A、B两点的间接可达距离IAB{C}=∑(LAC1,LC1C2,…,LCmB),A、B两点的间接可达距离并不唯一。

定义3 障碍距离.若A、B两点存在有限个不同的间接可达距离,则间接可达距离的最小值定义为A、B两点的障碍距离DO(A,B)。

当A、B相互不可见时,求解DO(A,B)的主要思想是采用递归的方法将点A到B的间接可达距离化分成三段,分别是A到障碍物Oi的间接距离、障碍物Oi到障碍物Oj的间接可达距离、障碍物Oj到B的间接距离,求解DO(A,B)即等价于求解以上三段的间接距离的最小值。我们可以预先计算出所有障碍物的顶点的间接可达距离,并排列成矩阵形式(矩阵命名为Mesh),Mesh矩阵可以作为预处理装载入程序中,这样每次求解不同的障碍物Oi到障碍物Oj的间接可达距离可以通过查找Mesh矩阵的元素直接得到,不需要重复运算,提高了算法的效率。

1.1 障碍距离的算法描述

定义任意两点p1、p2到单个或者多个障碍物的障碍距离,采用函数extdistance(bars,p1,p2)进行求解。

算法1 障碍距离的算法描述.

首先计算障碍物所有顶点的间接可达距离矩阵Mesh:

if p1和p2都是障碍物的顶点,对应barid1和barid2

if p1和p2在同一个障碍物上(barid1=barid2)

return p1和p2的障碍物绕边距离edgedistance(p1,p2)

else

Barid=(p1和p2的连线所穿越的障碍物集合)

if Barid为空,表示p1和p2为相互可见点

return distance(p1,p2)

end if

查找p1所在的barid1上面的扩展可见点集合Q

for each Qiin Q

计算dm(i)=edgedistance(p1,Qi)+extdistance(Qi,p2)

end for

返回 dm中的最小值min(dm)

end if

end if

每次Return将记录Mesh(p1,p2)的值。

然后根据上述已经计算的Mesh,计算任意两点之间的绕过障碍物的距离,算法如下:

if p1和p2都是障碍物顶点,

return Mesh(p1,p2)的值

end if

Barid=(p1和p2的连线所穿越的障碍物集合)

if Barid为空,表示p1和p2为直接可见点,

return distance(p1,p2)

else

选择p1和p2中不是障碍物顶点的一个,设为P2

计算p2针对这些障碍物Barid的最远可见点的集合Q

for each Qiin Q

计算dm(i)=distance(p2,Qi)+extdistance(Qi,p1)

end for

返回dm中的最小值min(dm)

end if

2 绕过障碍物的QPSO聚类算法

2.1 粒子逃逸原则

当检测粒子的某个聚类中心点时,如果发现陷入障碍物里,需将属于该聚类但在障碍物外的某个样本点与该粒子的聚类中心点连成线段,障碍物某条边与该线段的交点作为分界点。障碍物内的线段可以直接用欧氏距离公式计算并加权值ω,障碍物外的线段仍采用extdistance()函数求出障碍距离,将两段线段距离相加能够增大全局适应度函数值,使得选取的最优粒子绕过障碍,可以防止粒子再次落入障碍中。

2.2 绕过障碍物的QPSO聚类算法描述

在绕过障碍物的QPSO(Quantum-behaved Particle Swarm Optimization)聚类算法中,一个粒子代表Nc个聚类中心向量,每个粒子表示为:xi(mi1,…,mij,…,miNc),mij代表聚类Cij中第i个粒子的第j个聚类中心向量。粒子的适应度函数f(x)=∑∑d(x,c)2被定义为聚类算法中的量化误差。

算法2 绕过障碍物的QPSO算法.

(1)将输入的样本归一化处理,压缩到[0,1]内;

(2)依据样本数据,确定粒子群规模M;

(3)初始化粒子群。每个粒子,随机选取不在凸多边形内的Nc个聚类中心向量;

(4)对粒子群的个体最优和全局最优值初始化;

(5)从points中选取每个样本点向量,计算该样本点和粒子xi中所包含的每一个聚类中心向量的最短距离extdistance(bars,points(zp),xi);

(6)依据最近邻法则,将样本点归到类Cij;

(7)根据f(x)函数计算其适应度值;

(8)分别更新当前的pbest和gbest值;

(9)分别根据以下公式(1)、(2)、(3),得到新一代个体xi(t+1),如果xi(t+1)在凸多边形内,则采用粒子逃逸原则,更新xi(t+1);

pid=φ*Pid+(1-φ)*Pgd

(2)

(3)

(10)如果‖f(xi)(k+1)-f(xi)(k)‖<ε,算法结束,否则执行步骤(5)。

3 实验分析

3.1 测试说明

依据下面的三条规则来测试算法的性能:

(1) 定义的量化误差(即适应性函数)。

(2) 聚类内部的距离(Intra-cluster Distances),即一个聚类中数据向量之间的距离。

(3) 聚类之间的距离(Inter-cluster Distances),即聚类的中心向量之间的距离。

我们的目标是缩小聚类的量化误差,将聚类内部的距离减到最小,将聚类之间的距离增到最大。实验对带障碍的K-中心点算法、PSO优化的带障碍的K-中心点算法及绕过障碍物的QPSO数据聚类分别采用两组不同的样本数据和障碍物进行仿真实验及结果分析。

3.2 单个障碍物

第一组实验:在Matlab环境下,随机生成1个四边形障碍物及48个样本点数据,设定聚类数目为2,分别采用带障碍物的K-中心点算法、基于PSO的带障碍物算法、基于QPSO的带障碍物算法对48个样本点数据进行聚类。其中PSO算法的参数设置为:c1和c2取值为2,惯性权重ω取值0.8,粒子个数为20;QPSO算法的参数设置为:收缩扩张系数α从1.2线性减少到0.7,粒子个数为20,所有算法最大迭代次数均为MAXITER=1000,生成了第一组仿真实验结果。如图1、图2、图3所示,分别是带障碍的K-中心点算法、基于PSO的带障碍聚类算法、绕过障碍物的QPSO数据聚类的一次聚类结果。

图1 绕过单个障碍的K-中心点聚类

图2 绕过单个障碍的基于PSO的聚类算法

图3 绕过单个障碍的QPSO数据聚类

仿真实验表明,QPSO聚类算法使用粒子逃逸原则后,两个聚类中心点都避开了障碍物,同时依据上面介绍的三条规则,即量化误差、聚类内部之间的距离和聚类之间的距离来测试三种算法的性能,实验数据如表1。

表1 单个障碍物情况下的K-中心点、PSO、QPSO聚类算法性能比较

从表1中可以看出,在有一个障碍物的情况下QPSO算法的聚类结果中量化误差最小,K-中心点算法的量化误差最大,这说明基于QPSO的聚类算法可以寻找到比PSO算法和K-中心算法更好的全局最优值;从表1中还可以看出QPSO聚类算法的类内距离为0.1489,相比较其他两种算法,类内距离最小,这说明该算法的聚类内部数据比较紧密,数据间距比较小,聚类效果优于其它两种算法。另外,通过研究比较发现,绕过障碍物的聚类中心向量之间的距离并没有随着算法性能的提高而变大,而通常情况下类间距离越大表明算法的聚类效果越好,这说明类间距离不能有效的衡量绕过障碍物聚类的算法性能。

3.3 多个障碍物

第二组实验:在Matlab环境下随机生成三角形和四边形3个障碍物及45个样本点的数据,设定聚类个数为4,分别采用带障碍物的K-中心算法、基于PSO的带障碍物算法、基于QPSO的带障碍物算法对45个样本点数据进行聚类。其中算法的参数设置与第一组实验相同。

图4 绕过多个障碍的K-中心点聚类

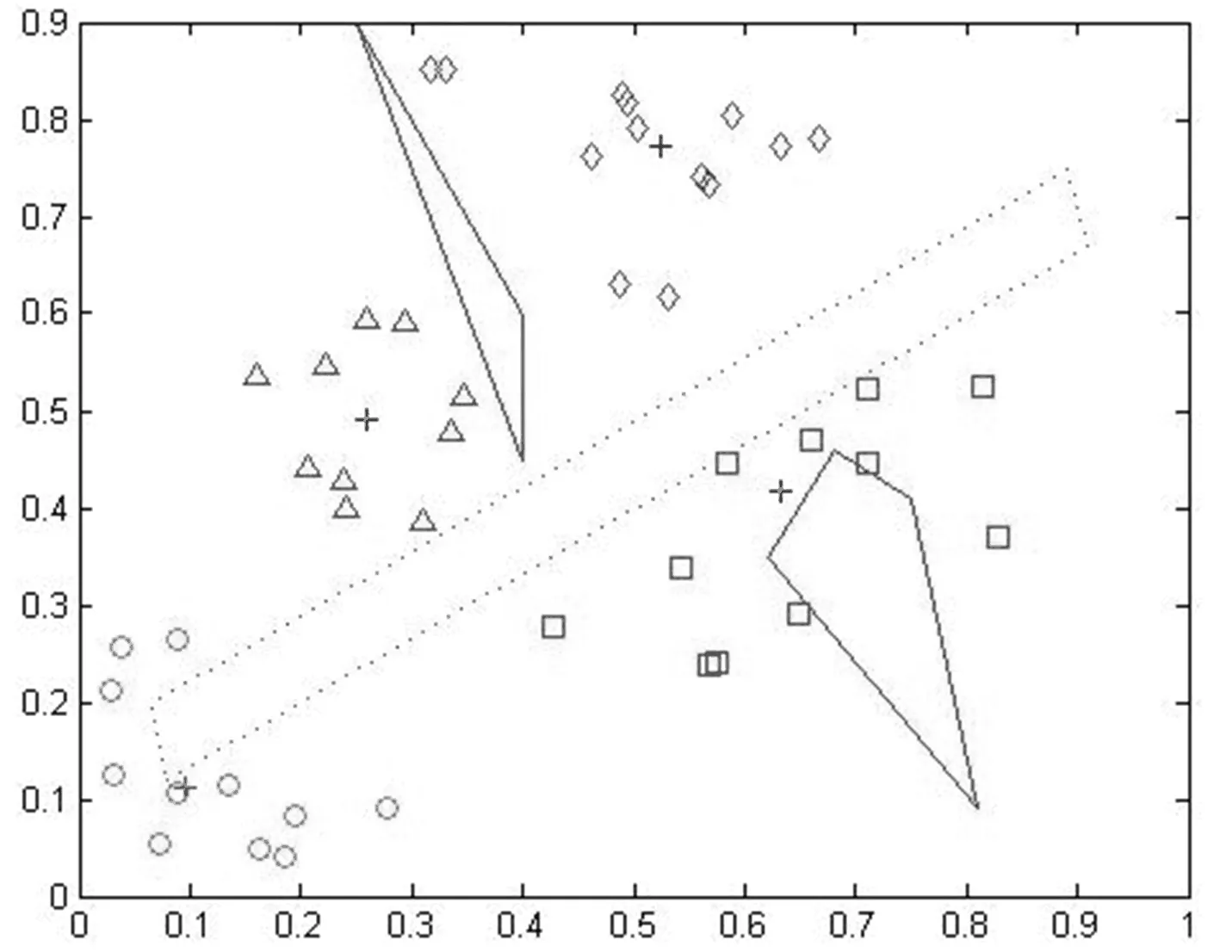
图5 绕过多个障碍的基于PSO的聚类算法

图6 绕过多个障碍物的QPSO数据聚类

图4、图5、图6分别是带障碍的K-中心点算法、基于PSO带障碍算法及绕过障碍物的QPSO数据聚类的最好聚类结果。同时依据上面介绍的三条规则来测试这三种算法的性能,实验数据如表2。

表2 三个障碍物情况下的K-中心点、PSO、QPSO聚类算法性能比较

仿真实验表明,三种算法在多个简单多边形障碍的情况下也是有效的,其结果具有实际意义。由表2中三种算法的量化误差和类间距离的数据比较表明,在多个障碍物的情况下QPSO聚类算法比基于PSO的算法和K-中心点算法表现出了更好的寻优能力。

3.4 实验分析

总体来说,绕过障碍物的QPSO数据聚类算法比较稳定,对初始值的敏感度不高,聚类中数据向量之间的距离之和比较小,保证了聚类内部比较紧凑。当粒子落入障碍物内部,采用粒子逃逸原则可以有效避免错误分类的情况发生,另外实验结果表明该算法比前两种算法更能有效控制粒子再次落入障碍物内的机率。

4 结束语

从两组实验对聚类中心点的初始化定义角度来看,把数据分成两类和四类,受经验值的影响比较大。因此今后还需要考虑加入无监督的聚类算法,比如SOM神经网络,通过聚类算法的自适应学习来调节分类中心点的个数达到提高和改善分类效果的目的。

[参 考 文 献]

[1] A.Tung，J.Hou，J.Han. Spatial Clustering in the Presence of Obstacles[M].Proc.17th Int'1 Conf．on Data Engineering，Washington：IEEE Computer Society，2001:359-367．

[2] V.Estivill-Castro，I.J.Lee.AUTOCLUST+：Automatic Clustering of Point-data Sets in the Presence of Obstacles[J].Temporal，Spatial，and Spatio-Temporal Data Mining，2000，20(7):133-146.

[3] Zai'ane O R，C.H.Lee.Clustering Spatial Data When Facing Physical Constraints[J].Proc.2nd IEEE Int'1 Conf.on Data Mining.Washington：IEEE Computer Society，2002:737-740．

[4] X.Wang，C.Rostoker，H.J.Hamilton. Density-based Spatial Clustering in the Presence of Obstacles and Facilitators[J].The 8th European Conference on Principles and Practice of Knowledge Discovery in Databases，2004，32(2):446-458.

[5] 张雪萍，王家耀．带障碍约束的遗传K中心空间聚类分析[J].计算机工程.2007，33(4):168-170.

[6] 李晓晴，焦素敏，张雪萍，等.基于粒子群优化的带障碍约束空间聚类分析[J].计算机工程与应用，2007)，28(24):5924-5927.

[7] 王纵虎，刘志镜，陈东辉.基于粒子群优化的模糊C-均值聚类算法研究[J].计算机科学，2012，39(9):166-169.

[8] 李朝锋，居红云，王琪.基于QPSO的模糊C均值聚类算法[J].微电子学与计算机，2008，25(7):194-197.