模糊值函数的极限及性质

郭兴梅， 张 慧

1 模糊值函数的极限的基本性质

在实分析学中,通过距离来研究实值函数的收敛性。在模糊分析学中为了研究模糊值函数的收敛性,也要引入相应的距离。为此,我们引入了文[5]中的模糊距离,并重新定义了模糊值函数的极限。进一步在普通的序关系意义下研究了模糊值函数的极限的基本性质,并给出了模糊值函数极限的存在条件。

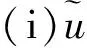
x,y∈R,t∈[0,1];

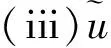
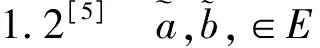
该模糊距离具有以下性质.

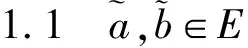
2 模糊值函数的收敛性及其性质

下面给出模糊值函数另一种极限的定义.

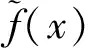
下面我们来讨论模糊值函数极限的性质.

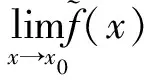
(1)

当0<|x-x0|<δ2时有

(2)

取δ=mim(δ1,δ2),则当0<|x-x0|<δ时(1)(2)同时成立。

进而对∀λ∈[0,1]有

由以上二式可得,对∀η∈[0,1]有

也即

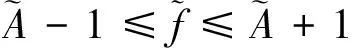
证明按假设,对任给的ε>0,分别存在正数δ1,δ2使得当0<|x-x0|<δ1时有

当0<|x-x0|<δ2时有

由上述不等式可得,对∀η∈[0,1]有

也即

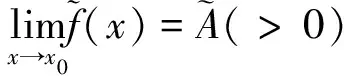
进而有

证明设

则对任给的ε>0,分别存在正数δ1,δ2使得当0<|x-x0|<δ1时对∀η∈[0,1]有

从而有

同理可得,当0<|x-x0|<δ2时有

进而有

(3)

(4)

由(3)(4)可得

由ε的任意性可得

由性质1.1容易验证以下结论.

3 模糊值函数的极限存在条件

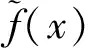
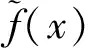
[参 考 文 献]

[1] 张文修.模糊数学基础[M].西安交通大学出版社,1984.

[2] 吴从炘,马 明.模糊分析学基础[M].北京国防工业出版社,1991:87-94.

[3] R.Goetschel and W.Voxman.Elementary fuzzy calculus[J]．Fuzzy.Set.Systems,1986,18:31-42.

[4] 郭嗣琮.基于结构元的模糊值函数的一般表示方法[J]．模糊系统与数学,2005,19(1):82-86.

[5] 张广全.Fuzzy数的Fuzzy距离与Fuzzy极限[J]．模糊系统与数学,1992,6:21-28.

[6] 张广全.模糊值测度论[M].北京:清华大学出版社,1998.

[7] 毕淑娟.模糊值函数的收敛性及连续性[J].哈尔滨商业大学学报:自然科学版,2002,18(3):330-333.

[8] 毕淑娟, 吴从炘.模糊数的运算性质及模糊数的距离与极限[J].模糊系统与数学,2000,14(3):40-44.

[9] 陈明浩.模糊分析学概论[M].北京:科学出版社,2008.