Ku波段宽带平行耦合微带线带通滤波器的设计

张维昊，张春荣，李 良，刘海强

(西安电子工程研究所 人力资源部，陕西 西安710100)

滤波器是一个二端口网络，通过在滤波器通带频率内提供信号传输，并在阻带内提供衰减的特性，用以控制微波/毫米波系统内某处的频率响应。典型的频率响应包括低通、高通、带同和带阻特性。滤波器实际已应用于各种类型的射频、微波、毫米波以及通信、雷达或测量系统当中。微带电路由于体积小、重量轻、频带宽、易与射频电路匹配等优点，近年来在滤波电路中得到广泛应用［1－2］。

本文根据分布参数滤波器设计原理，通过Matlab计算的滤波器结构参数，结合ADS2009的原理图与Momentum建模优化仿真，实现了Ku波段微带带通滤波器的快速设计方法［3］。文献［4］采用了与本文类似的方法，但得出的仿真图像在通带内平坦度与插入损耗均较差，且相对带宽均＜0.1，考虑实际生产时由加工等方面引起的误差，其滤波性能不一定能够保证。而文献［5～6］的方法虽然类似，但其频段均相对较低，且原理图仿真结果的带内平坦度较差。本文的优化参数设置能够保障滤波器具有足够的带宽，且带内平坦度与插入损耗均可满足需求，且现已应用于某工程项目之中。

1 理论模型

平行耦合微带线滤波器结构示意图如图1所示。其结构表现为由平行耦合微带线依次组成，每一段微带线均相当于一个半波长耦合组件，这是带通滤波器的基本组成单元。平行的间隙为耦合组件，耦合间隙在谐振线边缘可实现宽带耦合。滤波器结构为中心对称，每一个耦合节约为1/4波长［7］。其设计步骤如下。

图1 平行耦合微带线滤波器结构图

(1)确定低通原型。根据要求的带内波纹和衰减，选择适当的归一化低通原型，即巴特沃斯原型或切比雪夫模型，再确定滤波器阶次N以及归一化元件参数g1，g2，g3，…，gN，gN+1。

阶数N的确定由频率转化公式

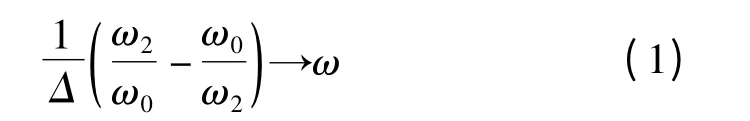
与归一化带宽公式

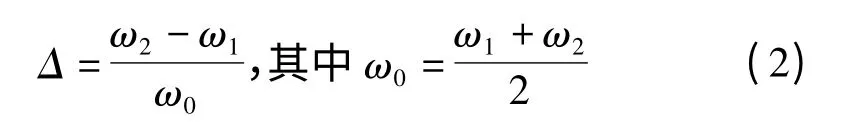
决定。其中，Δ为相对带宽;ω为指标中的衰减值对应的频率。

再经公式计算归一化频率Ω

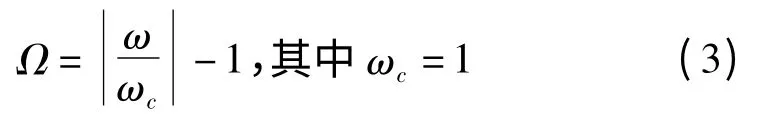
计算查询衰减与归一化频率的关系曲线，得出最适合的阶数N。N确定后，查表得出低通滤波器原型的元件值g1，g2，g3，…，gN，gN+1。

(2)计算导纳倒置器参量J。确定g1，g2，g3，…，gN，gN+1后，结合相对带宽Δ确定导纳倒置器参量J

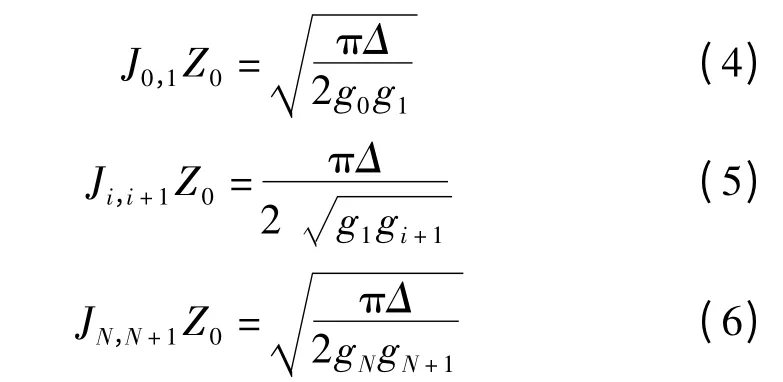
其中，Δ为相对带宽;Z0为输入输出端的特性阻抗，且1≤i≤N－1。

(3)计算奇偶模特性阻抗Ze，Zo。在得出导纳倒置器参量J后，通过公式

计算微带滤波器的奇模与偶模阻抗参量。

(4)根据特性阻抗值求解滤波器微带线尺寸与间隔。利用Matlab编写上述公式的计算程序，快速解算出所需的Ze与Zo值，并结合ADS中的LineCale工具可快速得到微带线的长度L，宽度W与间距S。

(5)优化与仿真。在ADS中建立原理图模型，并结合设计指标进行优化仿真，为达到实际投版生产效果，需结合Momentum仿真。

2 设计实例

滤波器指标:中心频率为16.1 GHz，带宽750 MHz，在12.4 GHz处衰减≥50 dB，在19.5 GHz处衰减≥40 dB。带内波纹0.5 dB，输入输出阻抗为50Ω，介质基片为Rogers 5880，厚度为0.508 mm。

由于该滤波器频段较高，且其应用环境为复杂电磁环境，考虑到实际加工的误差与冗余设计，根据工程应用需求，在此处将带宽按照1.6 GHz进行设计，目的是能留有足够的带宽以满足设计指标，且在实际应用时不会产生问题。

由设计指标可知，滤波器在19.5 GHz处衰减为－40 dB，波纹为0.5 dB。通带为15.3～16.9 GHz，带宽为1.6 GHz。根据式(1)与式(2)，取ω2=19.5，ω0=16.1，经计算Δ=10.062 5。由上述结果计算出归一化频率ω值，将ω代入式(3)中得出Ω=2.88。

由滤波器的带内波纹要求选择0.5 dB波纹的切比雪夫滤波器，根据衰减值与归一化频率的曲线关系，得出在Ω=2.88时，要达到衰减40 dB的指标，N值最小取N=4。为使边带更加陡峭，达到更好的滤波性能，此处取N=5。根据表1可得切比雪夫滤波器的元器件参数为［1－2］:g0=g6=1，g1=g5=1.705 8，g2=g4=1.229 6，g3=2.540 8。

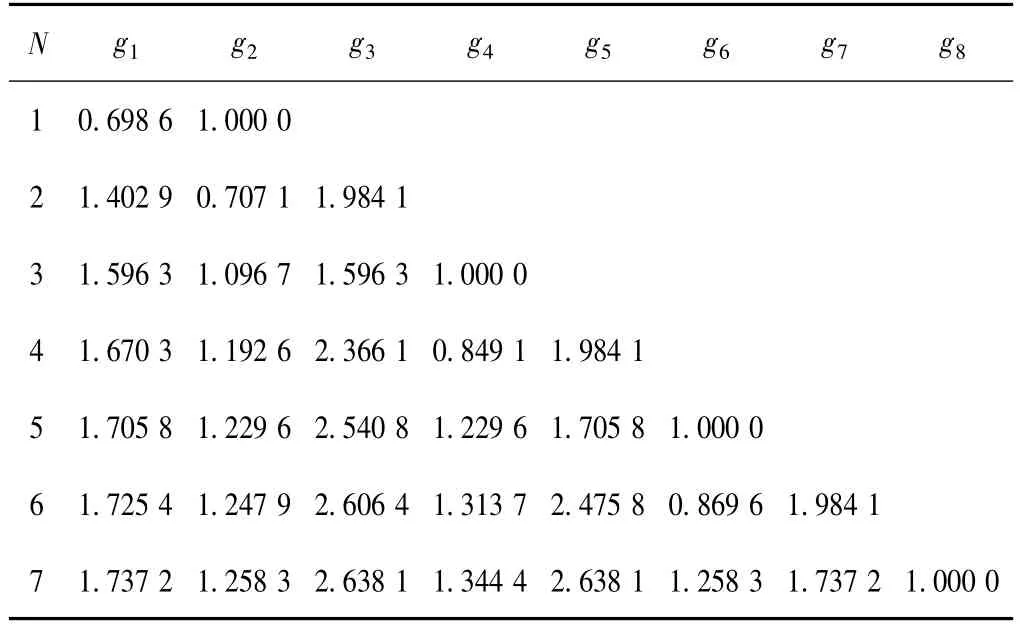
表1 切比雪夫滤波器原型的元件值(g0=1，ωc=1，波纹为0.5 dB)

将所有参数值代入式(4)～式(6)，经Matlab程序计算，得出导纳倒置器参量值J依次为

J0，1Z0=J5，6Z0=0.302 51，

J1，2Z0=J4，5Z0=0.107 79，

J2，3Z0=J3，4Z0=0.088 32。

将计算出的J值代入式(7)、式(8)中，通过Matlab程序计算奇偶模值如下

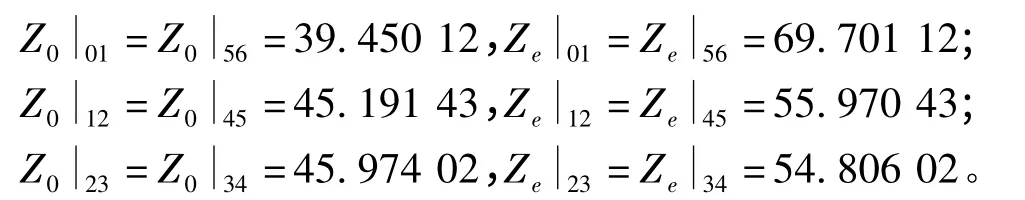
根据计算出的奇偶模值，通过使用ADS2009软件中自带的LineCal工具计算滤波器各节的长度L，宽度W以及其之间的缝隙宽度S，如表2所示。

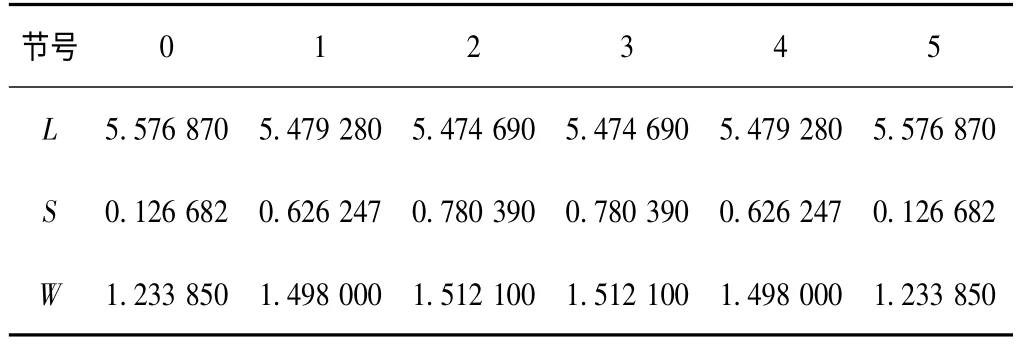
表2 微带线的初始尺寸值

在ADS2009中建立该滤波器模型，如图2所示，其中各节的尺寸参数与间隙均设置为可优化量。

将计算出的微带线尺寸值代入。由于耦合值估算会导致误差，并会导致仿真图形与预期图形存在较大的差异，此时需要使用优化工具Optim来使得原理仿真图像接近指标要求。

图3为使用Optim工具优化时的参量设置。

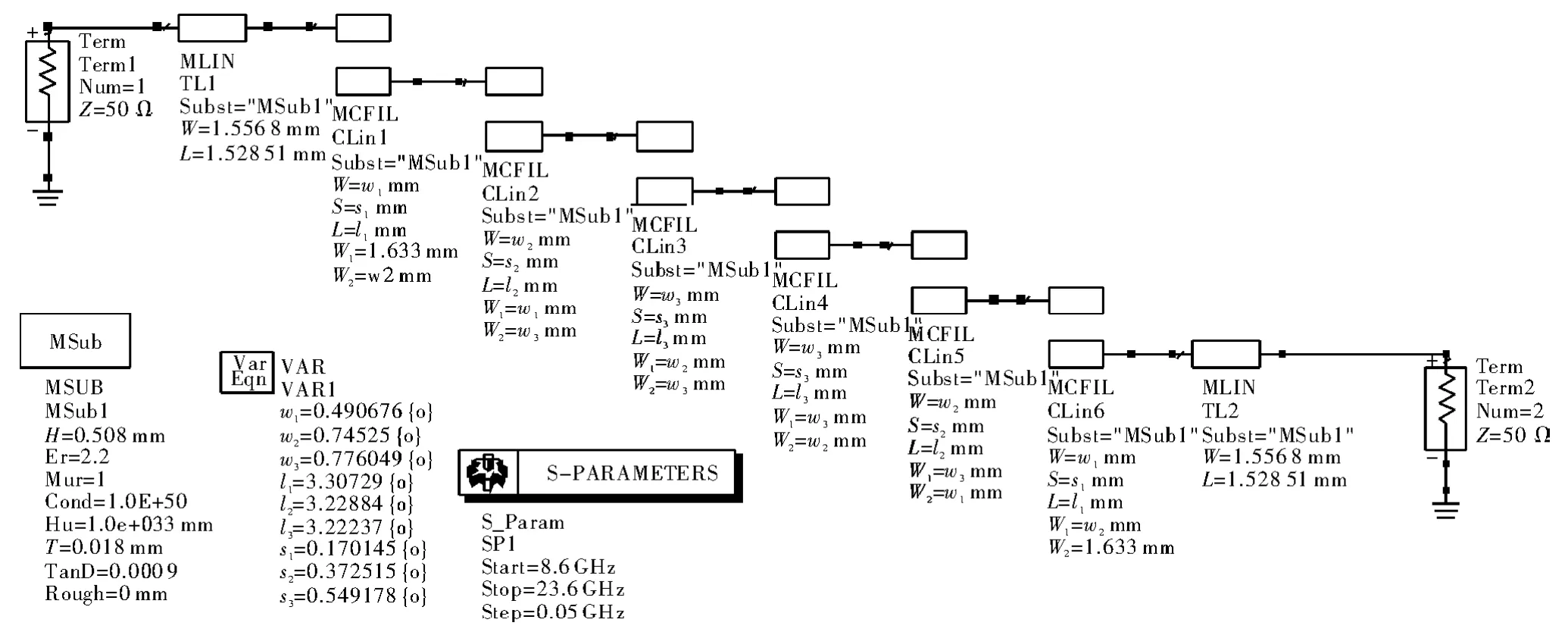
图2 平行耦合带线带通滤波器仿真设计原理图

图3 平行耦合带线带通滤波器仿真优化参数设置方式

设置目标Goal，除了通带上下边带与带外抑制指标外，还加入了对图形其他频段的优化目标，如图中对带外抑制的重点优化，使得带外抑制效果更加理想。设置完成后对原理图进行优化，使得仿真结果接近预期指标。如图4与图5所示，原理图仿真在通带内插损＜0.1 dB，带外抑制基本达到要求。

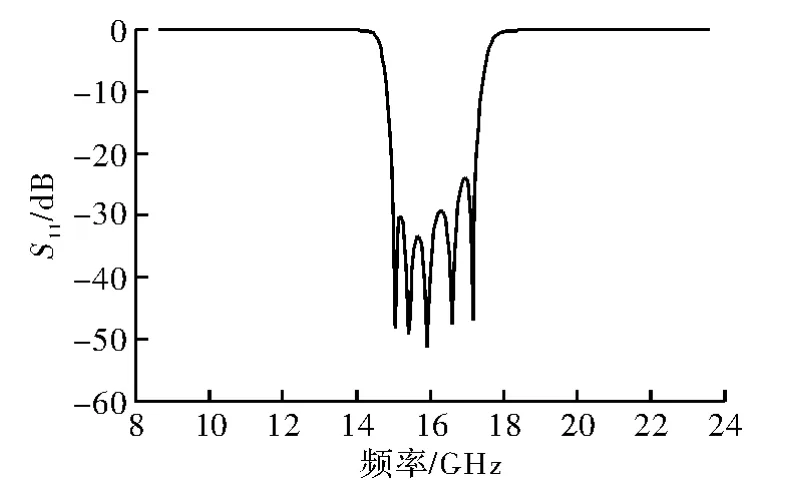
图4 原理图仿真S11参数图形

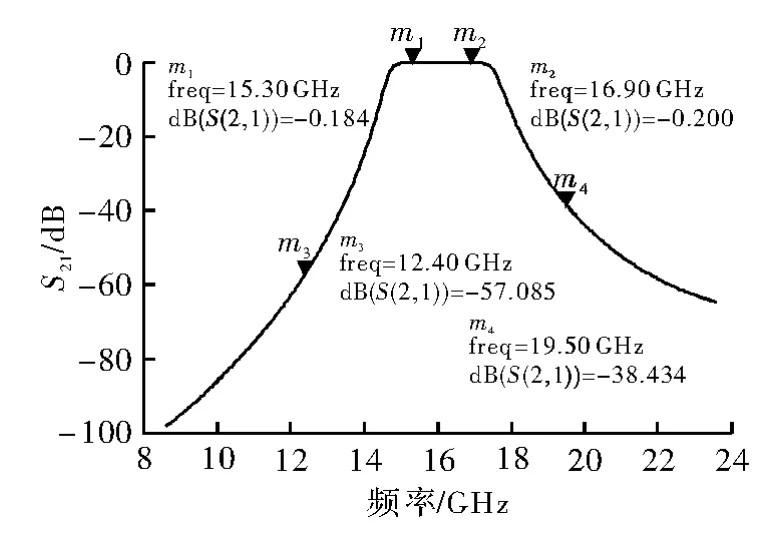
图5 原理图仿真S21参数图形

经优化后的滤波器尺寸如表3所示。

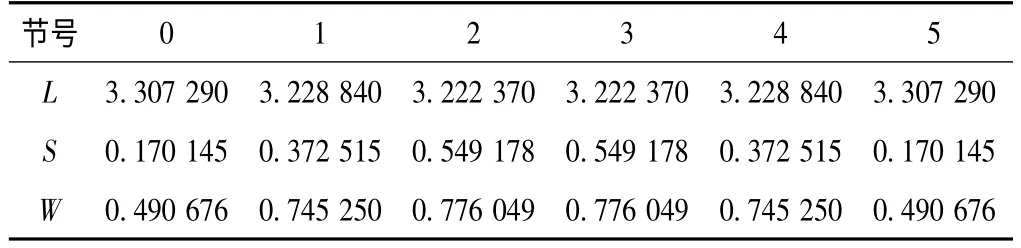
表3 微带线的优化后尺寸值

由于ADS2009原理图仿真时并未考虑耦合线节之间的相互作用，均因而与实际情况相比仍存在误差。Ku波段滤波器的尺寸已相当小，较小的尺寸加工误差均可能会使得S参数曲线发生大的变化。因此需要用Momentum进行版图仿真，使得结果尽量接近实际情况。

首先生成滤波器的版图，如图6所示。

图6 平行耦合带线滤波器版图

然后对版图进行仿真。由于ADS版图仿真采用矩量法进行计算，其结果的精确度较高，可作为投产前的参考。由图7与图8的仿真结果显示，在实际使用的通带中，滤波器的插入损耗在可接受范围内，带外抑制也同样满足要求。

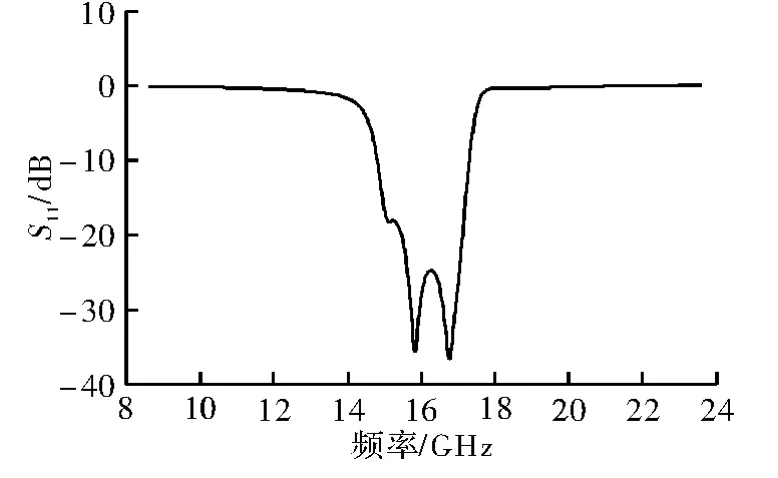
图7 滤波器版图仿真的S11曲线

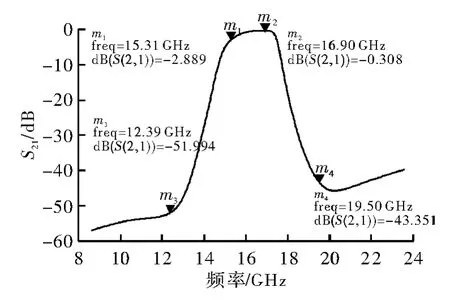
图8 滤波器版图仿真的S21曲线

由曲线图可看出，S21曲线在通带下边带的插入损耗过大，已达到了3 dB，这是由该型滤波器的特性决定的。而当频率＞20 GHz时，S21曲线开始有增大趋势，并应当会在二倍频处产生谐振。如何使通带变得更加陡峭且消除高次倍频的谐振，将是下一步的研究目标。

3 结束语

本文通过Matlab程序计算，结合ADS原理图仿真与Momentum版图仿真来进行Ku波段平行耦合微带线滤波器的设计。由于Ku波段频率较高，微小的尺寸差异会导致S参数变化过大，因此计算及优化工作就显得尤为重要。随着频段的不断升高，滤波器的结构以及尺寸对其性能的影响也越发明显。如何提高带外抑制、降低高次谐振和插入损耗等也是需要重点考虑，以上问题将在后续的研究中继续进行。

［1］DAVID M.Pozar微波工程［M］.3版.北京:电子工业出版社，2011.

［2］LUDWIG R.射频电路设计——理论与应用［M］.北京:电子工业出版社，2012.

［3］ 甘本袚.现代微波滤波器的结构与设计［M］.北京:科学出版社，1973.

［4］ 张琦，李裕，万国宾，等.Ku波段平行耦合线带通滤波器的仿真设计［J］.遥测遥控，2012，33(6):31－34.

［5］ 王海英，张福洪.微带抽头线发夹型带通滤波器的设计及优化［J］.电子器件，2012，35(3):334－338.

［6］ 张福洪，张振强，马佳佳.基于ADS的平行耦合微带线带通滤波器的设计及优化［J］.电子器件，2010，33(4):433－437.

［7］ 甘后乐，楼东武.平行耦合微带线带通滤波器的多步法优化设计［J］.微波学报2005，21(6):33－35.