3种雷达脉冲压缩信号的性能比较
石志敏
(西安电子科技大学 电子工程学院,陕西 西安710071)
脉冲压缩作为雷达信号处理的关键技术之一,其有效解决了距离分辨力与平均功率之间的矛盾。脉冲压缩就是在雷达发射机中发射时宽较宽、峰值功率较低的脉冲,通过对载频进行编码以增加发射波形的带宽;然后在接收机中对回波实施脉冲压缩,从而达到窄脉冲、高峰值功率的简单脉冲体制雷达所具有的分辨能力和探测性能[1]。
在脉冲压缩技术中,雷达所使用的发射信号波形的设计,是决定脉冲压缩性能的关键。常用的发射信号波形分为:线性调频(LFM)信号,非线性调频(NLFM)信号和相位编码(PSK)信号等[2-4]。
1 脉冲压缩的基本原理
作为雷达发射信号,其均为实信号,但为了雷达信号处理的方便则常常用复信号来表示,即

脉冲压缩为将输入的复包络信号通过一个相应的匹配滤波器后得到输出的过程。则滤波器的脉冲响应函数为

其中,H(f)是任意滤波器对复包络的传递函数。那么输入信号u(t)通过滤波器的输出波形为



时滤波器将在t0时刻输出一个尖峰,则所得的滤波器为匹配滤波器。同时可以看出,当t0=0时,匹配滤波器的脉冲响应h(t)为输入的复包络信号u(t)的时间倒置的复共轭[1-2]。
2 3种信号形式
2.1 线性调频信号
线性调频(LFM)信号的数学表达式为


图1 典型的Chirp信号
将式(5)中的up-chirp信号重写为

是信号s(t)的复包络。由傅里叶变换性质,S(t)与s(t)具有相同的幅频特性,只是中心频率不同,因此仿真时,只需考虑S(t)[3]。
2.2 非线性调频信号
非线性调频信号是通过改变传统线性调频信号在不同时刻的调频率来实现对信号功率谱的加权,从而改善脉压性能。
正弦调频(SFM)信号的数学表达式为

其中,Am为幅度;f0为载波频率;fm为调制频率;mf为调制系数,定义为Δf为最大频偏。mf的大小影响着信号的频谱性质及形状。
正弦调频信号的瞬时自相关函数为

2.3 相位编码信号
相位编码信号的相位调制函数是有限个离散值,通常由伪随机序列构成。相位编码信号由n个相互连接的高频子脉冲组成,这些子脉冲宽度相等、频率相同。本文用到的相位编码信号为二相编码信号,即各自的初相位只取0、π两个数值。二相编码信号数学表达式为
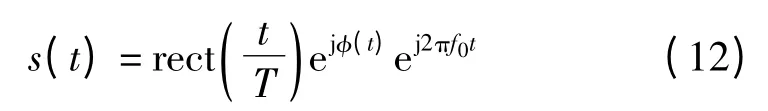
其中,f0为载波频率;φ(t)为相位函数,在0、π两个值之间变化,即信号的复包络在-1和1之间变化。s(t)的复包络可表示为

其中,v(t)为子脉冲函数;τ为子脉冲宽度;cn为编码序列;N为编码序列长度,信号时宽T=Nτ。二相编码信号的频谱表示为

由上可看出,二相编码信号的频谱主要由子脉冲的频谱决定,而且与编码形式有关。现在可以找到的最长巴克码的长度为13[8]。
3 Matlab仿真分析及比较
本文选取了3种雷达脉冲压缩信号进行仿真。除发射信号外其余的各个过程都相同。
下面给出线性调频(LFM)信号的脉冲压缩结果。仿真参数:采样频率fs=2 GHz,脉冲宽度T=0.5μs,脉冲重复周期PRI=50μs,中心频率f0=1 GHz,雷达发射功率Pt=1 MW,带宽B=20 MHz,其时宽带宽积为10>1,符合脉冲压缩条件,如图2所示。

图2 线性调频信号脉冲压缩
下面给出正弦调频(SFM)信号的脉冲压缩结果。采用的仿真参数:采样频率fs=2 GHz,脉冲宽度T=0.5μs,脉冲重复周期PRI=50μs,中心频率f0=1 GHz,雷达发射功率Pt=1 MW,调制系数mf=1,调制频率fm=1 MHz,如图3所示。

图3 正弦调频信号脉冲压缩
图4给出相位编码(PSK)信号的脉冲压缩结果。采用的仿真参数是:采样频率fs=2 GHz,脉冲宽度T=0.5μs,脉冲重复周期PRI=50μs,中心频率f0=1 GHz,雷达发射功率Pt=1 MW,巴克码长度为13(1 1 1 1 1-1-1 1 1-1 1-1 1)。
在给定的仿真参数下对3种信号脉冲压缩效果进行比较分析:
(1)由图2~图4的(a)可以看出,相位编码信号产生的脉冲压缩幅度最高,脉压效果最好,但图4相位编码信号第一个信号的旁瓣较高会掩盖能量较弱的小信号,对信号检测有较大影响。
(2)图2中线性调频信号也会有旁瓣的影响。在时宽带宽积不高的情况下脉压的效果不理想。
(3)由图3所示正弦调频信号主旁瓣比可达70 dB,旁瓣对弱信号影响较小。同时脉冲压缩的幅度较高可以满足对脉压的要求。综合考虑在此仿真参数下非线性调频信号的效能最优。

图4 相位编码信号脉冲压缩
4 结束语
综上所述,本文对3种雷达脉压信号进行了分析与比较,在设定相同的仿真参数的条件下,比较发现正弦调频信号的效果最好。同时也发现,不同反射信号的波形对脉冲压缩的效果有较大的影响,因此,今后可以继续对不同波形的信号进行比较,或对多个已知信号的组合来观察分析其脉冲压缩效果。
[1] 张明友,汪学刚.雷达系统[M].北京:电子工业出版社,2006.
[2] 万小燕.雷达中常用的波形设计及数字脉压的工程实现[J].现代电子技术,2007,30(13):29-31.
[3] 朱守中,储彬彬,漆德宁.雷达脉冲压缩信号仿真分析[J].电子质量,2009(5):33-35.
[4] 徐玉芬.现代雷达信号处理的数字脉冲压缩方法[J].现代雷达,2007,29(7):61-64
[5]BLUNT S D,GERLACH K.Adaptive pulse compression repair processing[C].2005 IEEE International Radar Conference,2005:519-523.
[6] 阮黎婷.非线性调频信号的波形设计与脉冲压缩[D].西安:西安电子科技大学,2010.
[7] 吕远.复杂调制雷达信号的调频识别与参数估计算法研究[D].成都:电子科技大学,2009.
[8] 徐景明,朱灿焰.两种雷达脉冲压缩信号的性能分析[J].兵工自动化,2010,29(8):60-63.

