基于压缩感知的空域信号DOA估计
郭月强,陈建春,王永军
(西安电子科技大学 电子工程学院,陕西 西安710071)
波达方向估计(DOA)是阵列信号处理中的重要研究内容之一,在雷达、声纳、通信等领域均得到了广泛应用。自20世纪60年代起,研究者们提出了多种有效的DOA估计算法,主要有Capon最小方差法以及Schimidt等提出的以多重信号分类(MUSIC)算法为代表的子空间类算法。近年来,由Donoho等人提出的压缩感知(Compress Sensing,CS)理论[1-2]受到了关注,已被广泛应用于图像处理、通信等领域[3-4]。压缩感知理论指出若信号是可压缩的或稀疏的,则可利用远低于奈奎斯特频率的采样速率对信号进行采样,通过求解一个l1最小范数优化问题,以较高的概率精确重构原信号[5]。实际中空域感兴趣的目标信号只占据少量的角度分辨单元,相对于整个空间而言目标在空域内是稀疏的,因此压缩感知[6]理论在DOA估计中也得到了广泛研究。针对以上问题,文中提出一种新的基于奇异值分解的多矢量欠定系统聚焦求解算法(SVDMFOCUSS),实现了DOA高分辨估计。
1 压缩感知理论
1.1 信号稀疏性表示
CS理论成立的前提是信号为稀疏或可压缩的[7-8]。为简化模型,以便更清楚地描述信号的稀疏表示问题,仅考虑长度为N的实信号x,且有x=[x1,x2,…,xN]T。根据矩阵理论可知,x可用一组正交基Ψ=[Ψ1,Ψ2,…,ΨM]的线性组合表示,设对应的系数为si,i=1,2,…,N,则有

式中,si=<x,Ψi>,s与x为N维列向量,Ψ为N×N维矩阵。若信号x在基Ψ下仅有K(K≪N)个非零或远大于零的系数时,则称信号x为基Ψ上的稀疏信号。
1.2 投影测量矩阵设计
在CS理论中,通过变换得到信号的稀疏系数s=Ψ-1x后,需设计一个投影测量矩阵Φ。Φ必须保证:对信号x在该投影测量矩阵上进行投影得到M个投影测量值,且该M个测量值含有信号x大部分的信息,从而可使用少量的投影测量数据精确地重构信号x。
在压缩感知测量模型中,并不是对稀疏信号x本身进行直接采样,而是将x映射到投影测量基Φ=[φ1,φ2,…,φM]T上,得到投影测量值ym=<x,φm>,m=1,2,…,M。用矩阵形式表示为

其中,φm为N维列向量;y为M维列向量;Θ为M×N(M≪N)维矩阵;Φ称为感知矩阵或测量矩阵。目前,可用于压缩感知的测量矩阵主要有高斯随机矩阵和二值随机矩阵。
对于多快拍接收数据情况,设阵列接收快拍数为N,第i次快拍接收的信号矢量为yi,稀疏系数矢量为si,噪声矢量为ni,且服从正态分布,即ni~N(0,σ2I),由式(2)可得

其中,Y=[y1,y2,…,yN],S=[s1,s2,…,sN],N=[n1,n2,…,nN]。
1.3 稀疏信号重构算法
稀疏信号重构是从少量的观测数据中重构原始信号,即从长度为M的观测数据中重构长度为N(M≪N)的原始信号。在信号重构过程中,由于观测数据长度M远小于信号的长度N,因此必须要面对求解欠定方程(2)的情况。理论上,最简单的方法是求解l0最小化范数问题
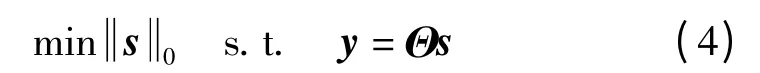
式(4)所示为s的l0范数问题,实际上是求解向量s中非零元素的个数。l0最小化范数问题从理论上看是最优的,但在实际中却难以实现,是一个NP难问题。
文献[9]指出,求解一个更简单的l1最优化问题可以产生与l0最优化问题等价的解
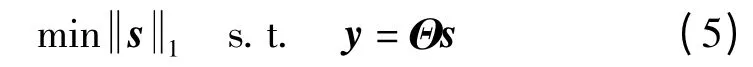
式(5)所示为s的l1范数问题,式(5)与式(4)只有很小的不同,但却使得问题变成了求解一个凸优化问题,可简化为线性规划问题。求解该优化问题的典型算法有:基追踪(BP)算法、正交匹配追踪(OMP)算法及多矢量欠定系统聚焦求解(MFOCUSS)算法等。
2 SVD-MFOCUSS算法
2.1 稀疏信号模型的降维表示
将式(3)的阵列接收数据矩阵Y用SVD分解表示为

对式(6)保留一个降维后的M×K维矩阵YSV,YSV保留了信号大部分的能量,且有

式中,DK=[IK,0]T,IK为K×K维单位矩阵;0为K×(T-K)维零矩阵。令SSV=SVDK和NSV=NVDK,则
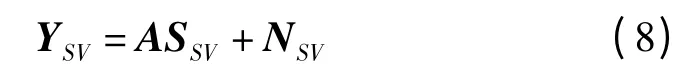
比较式(3)和式(8)可知,阵列接收数据矩阵由M×NL维降低至M×K维,实际情况中,有K≪NL,因此通过求解式(8)进行DOA估计比直接求解式(3)运算量显著降低。此外,SVD分解本质上是一个信号分量累积的过程,这使得在低信噪比情况下也可采用稀疏重构算法进行有效的DOA估计。
2.2 稀疏信号模型优化求解
实际中目标信号在空域是稀疏的,在n个快拍期间,目标信号未跨角度单元移动,即在式(3)中有,,si与sj(i≠j)的非零元素位置相同,故S中仅有K行非0,其余的M-K行为0,所以S为行稀疏矩阵。由于SSV=SVDK的右乘矩阵为阵列初等变换,故SSV与S具有相同的系数特征。类似于信号矢量稀疏性的描述,稀疏矩阵行的稀疏特性可用其非零行的个数描述,即
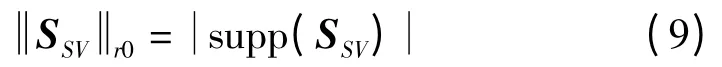
因此,用MFOCUSS算法对稀疏问题(8)中的SSV进行估计,得到SVD-MFOCUSS算法的谱估计公式为
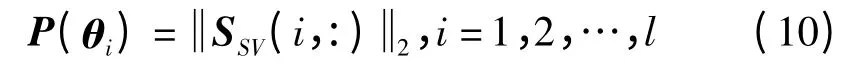
3 仿真实验分析
实验1考察两个相邻的非相干信号DOA估计情况,信号的入射角度分别为20°、22°,阵元数为8,阵列接收快拍数为200,信噪比为10 dB。图1为Beamforming算法、Capon算法、MUSIC的算法和SVD-MFOCUSS算法的空间频谱对比。由图1可看出SVD-MFOCUSS算法能有效分辨邻近目标信号,而Beamforming算法、Capon算法及MUSIC算法无法分辨这两种邻近目标,即说明SVD-MFOCUSS算法具有更高的角度分辨力。
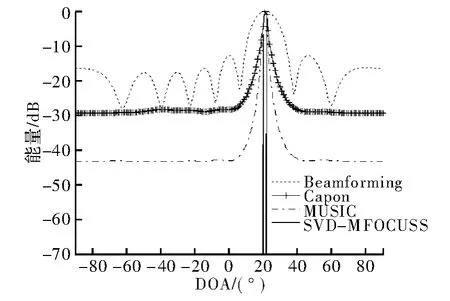
图1 相邻非相干信号的空间谱估计
实验2比较各算法在不同信噪比情况下的DOA估计性能,信号入射角度分别为20°、30°,阵元数为8,阵列接收快拍数为200,信噪比分别为-10 dB和20 dB。图2为各算法在-10 dB时的空间谱估计对比。图3为各算法在20 dB时的空间谱估计对比。对比图3和图4可看出,在20 dB情况下,Capon算法、MUSIC算法和SVD-MFOCUSS算法可分辨两类信号,而Beamforming算法融合了两个谱峰;而在-10 dB情况下,唯有SVD-MFOCUSS算法和MUSIC算法可分辨两个信号,而Beamforming算法和Capon算法都融合了两个谱峰。由此说明SVD-MFOCUSS算法在低信噪比情况下同样具有良好的DOA估计性能。
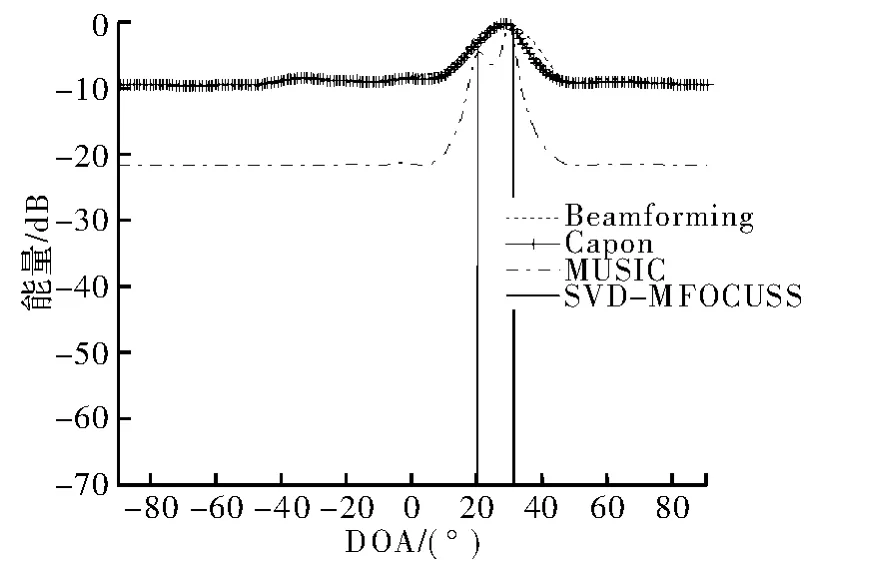
图2 -10 dB时的非相干信号空间谱估计
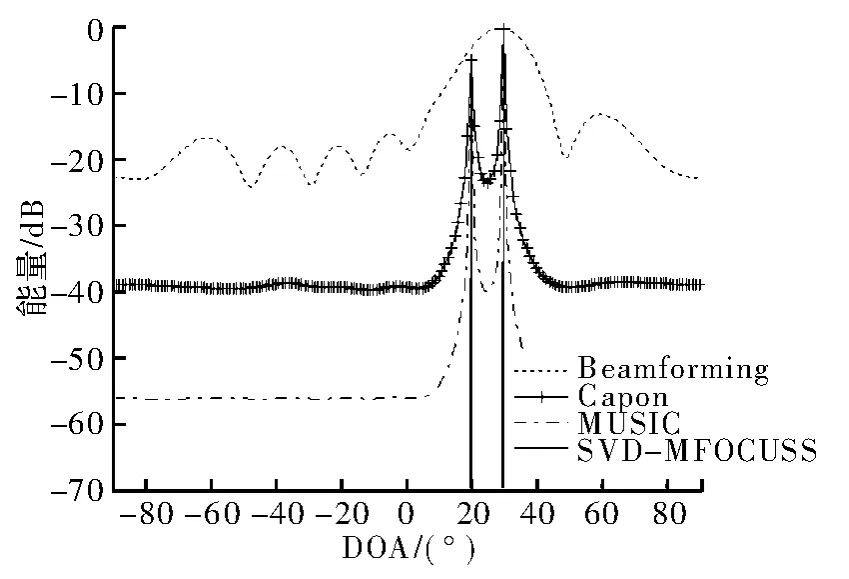
图3 20 dB时的非相干信号空间谱估计
实验3考察相干信号的DOA估计情况,信号入射角度分别是20°、20°,阵元数为8,阵列接收快拍数为200,信噪比为20 dB。比较图4和图5可看出,在非相干信号情况下,Capon算法、MUSIC算法和SVDMFOCUSS算法可分辨出两个信号;在相干信号情况下,SVD-MFOCUSS算法任然可精确分辨出两类信号,而其他算法的DOA估计性能明显下降。
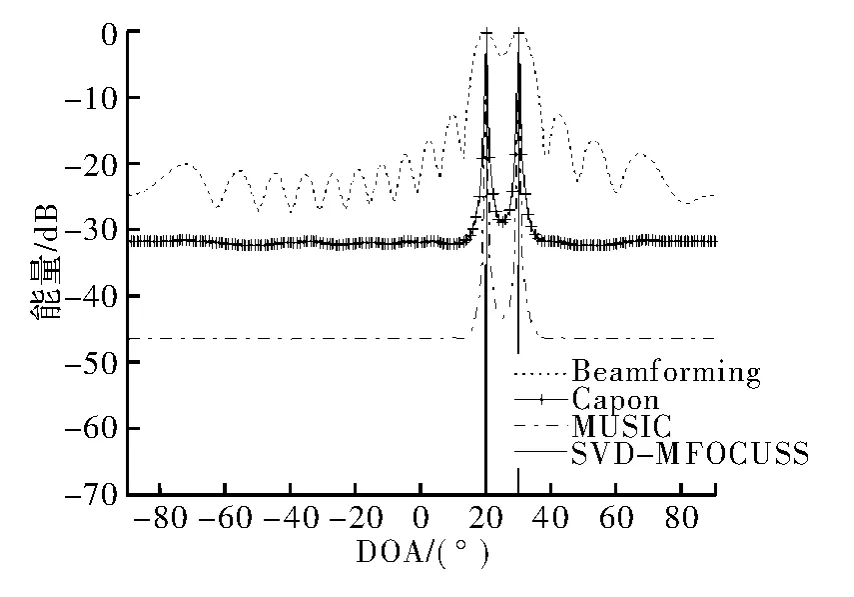
图4 非相干信号空间谱估计

图5 相干信号空间谱估计
4 结束语
提出一种新的基于CS的DOA估计算法,SVDMFOCUSS算法本质上是采用奇异值分解进行信号降维及能量积累,改善了传统稀疏信号恢复算法的应用范围,可在低信噪比情况下使用,且明显降低了计算量;同传统的DOA估计算法相比,SVD-MFOCUSS算法能对任意相干信号进行高分辨DOA估计,且具有良好的估计性能。
[1]DONOHOD.Compressed sensing[J].IEEE Transation on Information Theory,2006,52(4):1289-1306.
[2]CANDÈS E.Compressive sampling[C].Madrid,Spain:Proceedings of the International Congress of Mathematicians,2006.
[3]ROMBERG J.Imaging via compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):14-20.
[4]PAREDES J L,AREW G R,WANG Z M.Ultra-wideband compressed sensing:channel estimation[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(3):383-395.
[5]CANDÈS E J,WAKIN M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):14-30.
[6]CANDÈS E J,ELDER Y C,NEEDELL D.Compressed sensing with coherent and redundant dictionaries[J].Preprint,Applied and Computational Harmonic Analysis,2011,31(1):59-73.
[7]COTTER S F,RAO B D,ENGAN K,et al.Sparse solutions to linear inverse problems with multiple measurement vectors[J].IEEE Transactions on Signal Processing,2005,53(7):2477-2488.
[8]PEYRÈG.Best basis compessed sensing[J].Lecture Notes in Computer Science,2007,48(5):80-91.
[9]DONOHO D L,ELAD M,TEMLYAKOV V N.Stable recovery of sparse overcomplete representations in the presence of noise[J].IEEE Transactions on Information Theory,2006,52(1):6-18.

