双通道接收机空间谱估计中的理论实现

张 玮，赵益民，张 敏

(西安电子科技大学 电子工程学院，陕西 西安710071)

空间谱估计［1］有多种实现方法，这些算法在众多领域已得到广泛研究于发展，它们不仅能区分非相干信号，同时也能区分相干信号。对于这一类特征结构类算法，其均是基于协方差矩阵分解。因此，无论其中的哪一种算法，得到其相应的协方差矩阵，便可应用该算法进行波达方向的估计。

1 原理

通常情况下，获得阵列协方差矩阵的方式为:使一个阵元对应于接收机的一个通道，即一个阵元连接一个接收机，在获得不同时刻每个阵元上接收的信号后，便可得到阵列的采样协方差矩阵。但是，该方法有其较大的缺点。即随着阵元数目的增加，接收机数目也随之增加，这便使得该接收系统造价变得昂贵。且由于上述的特征结构类算法对模型误差较为敏感。所以，要保证所有的接收通道均不引入附加相移，即实现通道一致性较为困难。应用自适应阵列信号接收处理相类似的方法，依据自适应阵的输出，再利用权微扰算法便可实现在接收机数量较少的情况下得到阵列的协方差矩阵［2］。

自适应阵列信号处理中有如下公式

式中，X(t)是阵元的响应;y(t)是阵列的总输出;WH是权矢量的复共轭转置。

阵列输出的数据协方差矩阵为

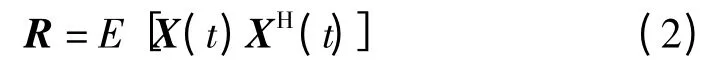
其中，E代表期望。而集合平均与单次实现的平均对平稳随机信号和确定信号提供相同的结构。因此，有

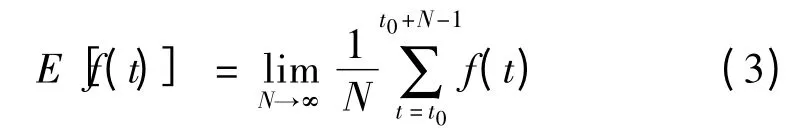
接收机的输出功率是

当来自n个阵元的输出信响应被同时测得时，数据协方差矩阵R是用采样协方差矩阵替代的，即

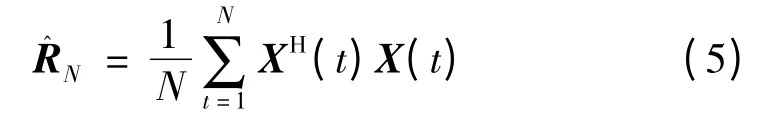
下面介绍多信号双通道接收机的实现，结构如图1所示。通过适当的加权以及权微扰，可得两个输出y+(t)和y－(t)。在适当加权的情况下，可通过y+(t)和y－(t)来获得阵列的协方差矩阵。

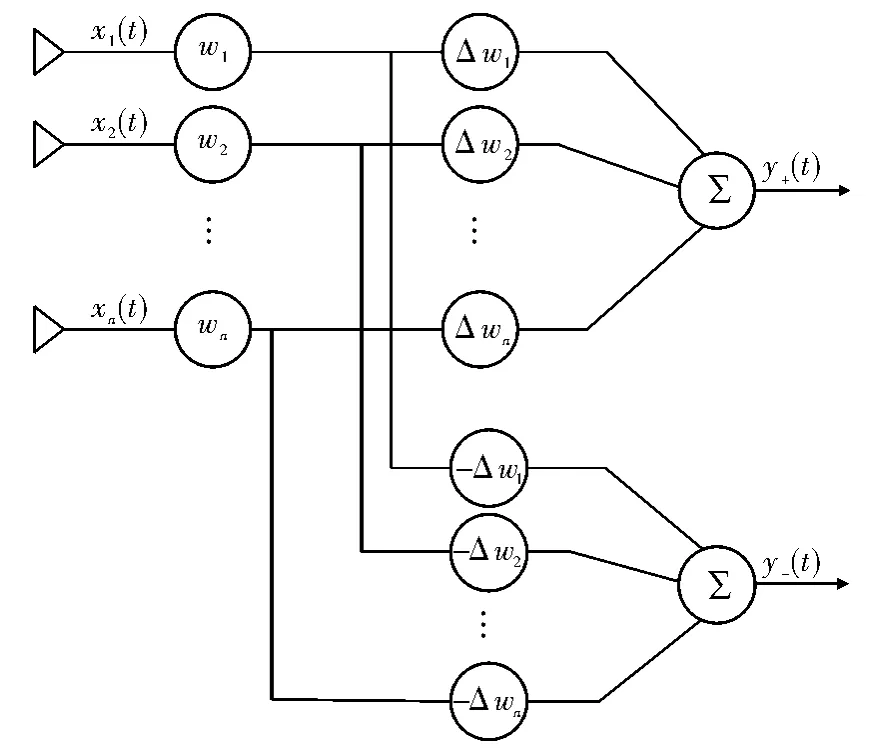
图1 双通道接收机示意图

取W+=Wnom+ΔW和W－=Wnom－ΔW，其中Wnom为标准权，ΔW为标准权的权扰动量。由该权扰动ΔW可得

其中，y+(t)和y－(t)是分别使用权W+和W－时的输出;而ynom(t)是ΔW=0时的输出，因为此时W+=W－=Wnom。通过对权扰动ΔW的适当选择，R的各元素可通过输出进行估计，从而得到其协方差矩阵，进而求解入射信号的到达角。

2 阵列协方差矩阵的权扰动算法

求解阵列的协方差矩阵，首先给出了协方差矩阵的性质:矩阵R为轭米特阵，即R=Rr+iRi，式中Rr为对称阵，Ri为反对称阵()。在具体的某些情况下，可利用R更进一步的结构，使求解过程简化。例如，在均匀直线阵及非相干信号源的情况下，R为Toeplitz结构。这里只需介绍一般情况下的轭米特阵。

假设权扰动ΔW=ΔWr+iΔWi，经化简整理可得下式

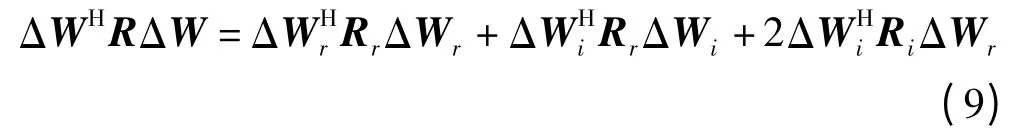
具体证明过程中，应注意利用协方差矩阵R的性质。

由式(9)，选择合适的ΔW即可得到协方差矩阵R。然而利用该式可通过有无限多种ΔW的选择方式获得R，下面介绍一种易于实现的方案:

(1)置ΔWr=ei(ei=(0，…，1，…，0)T，其中第i个元素为1，其他元素为0)，ΔWi=0，容易看出，Rr的第i个对角线元素等于ΔWHRΔW的值。

(2)置ΔWr=ei+ej和ΔWi=0，则j＞i时，Rr的元素Rr(i，j)可用式(10)来求得

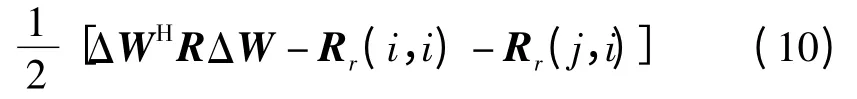
(3)根据Rr的对称性可以得到其剩余的元素，即可得到完整的Rr。

(4)由于Ri具有反对称性，所以Ri对角线上的元素皆等于0。

(5)置ΔWr=ej和ΔWi=ei，则j＞i时，Ri的元素Ri(i，j)可由式(11)求得

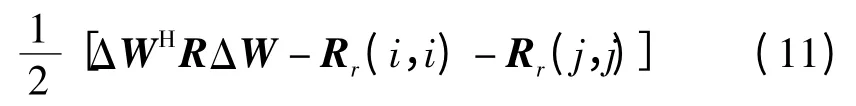
(6)根据Ri的反对称性可以得到其剩余的元素，即可得到完整的Ri。

(7)由于R=Rr+iRi，根据Rr和Ri即可得到协方差矩阵R。

与单通道接收机相比，该过程所需的扰动次数减少了1/2，更易于完成。且ynom(t)的值可由两个接收信号取平均求得，利于一致性的实现。通过利用所得的阵列协方差矩阵，便可运用特征结构类算法求解信号的波达方向［3］。

3 算法的实现流程

(1)产生信号X(t)。(2)获得阵列的标准权矢量矩阵Wnom，令ΔW=0，可得阵列在标准权时的输出ynom。(3)取ΔW(即ΔWr和ΔWi)为适当值，得权微扰时的输出y+和y－。(4)利用所得ynom、y+和y－根据式(7)可得ΔWHRΔW。(5)根据上节给出的方案，求Rr和Ri的各元素得协方差矩阵。(6)求N=，比较N和的各元素。(7)对协方差矩阵做特征分解，利用MUSIC算法获得信号的DOA估计［4－5］。

4 计算机仿真模拟及分析

根据上一节中给出的步骤对信号进行DOA估计仿真，其中给出阵元数为8，信号源数为3，则在不同信噪比、不同角度间隔下可由模拟结果大体推测该种方法的性能。

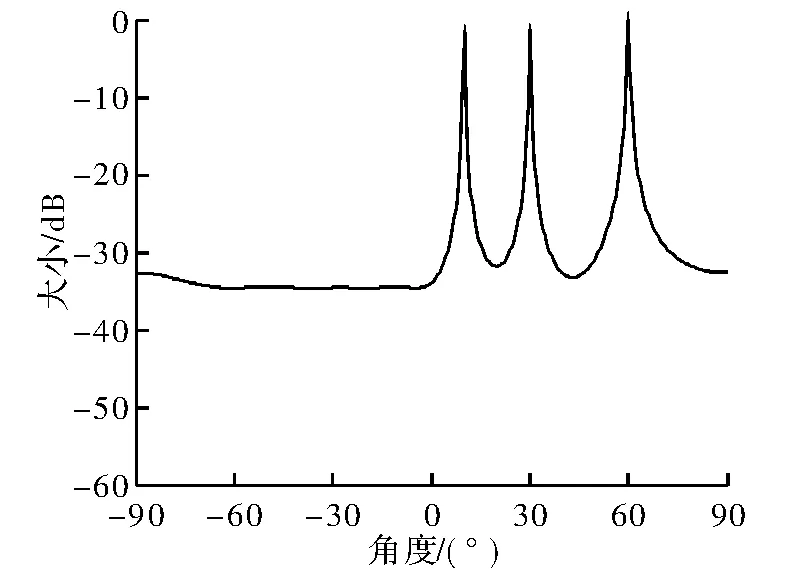
图2 信噪比为10，角度为10°、30°、60°

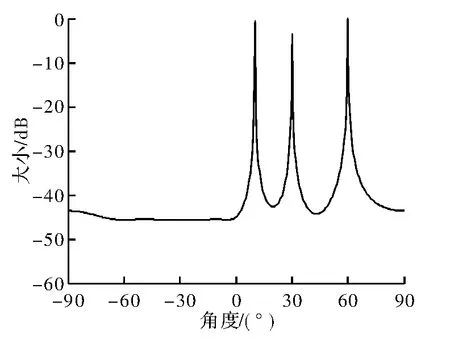
图3 信噪比为20，角度为10°、30°、60°

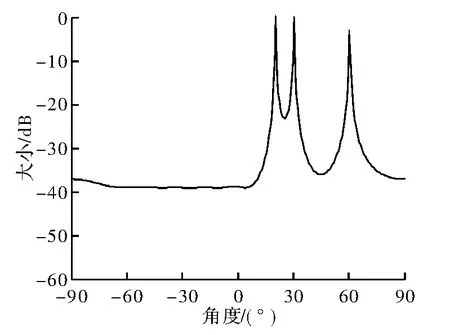
图4 信噪比为10，角度为20°、30°、60°

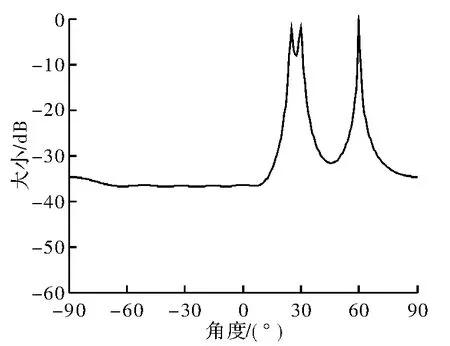
图5 信噪比为10，角度为25°、30°、60°

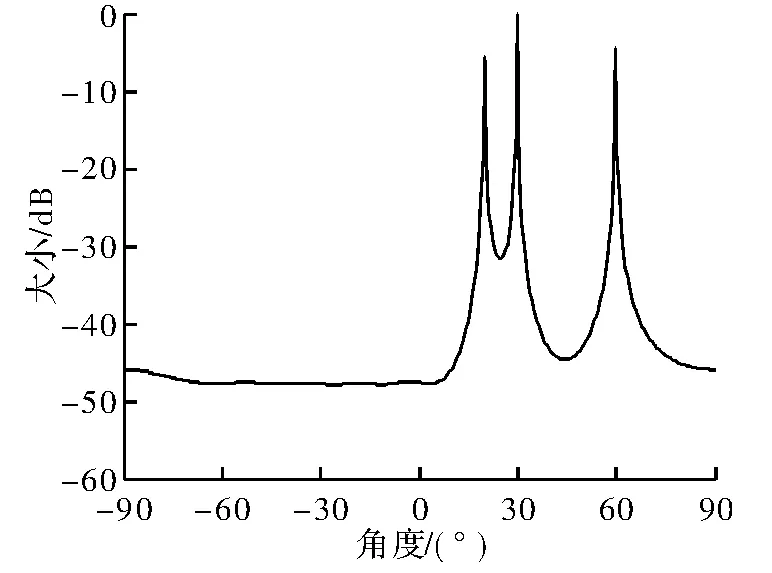
图6 信噪比为20，角度为20°、30°、60°

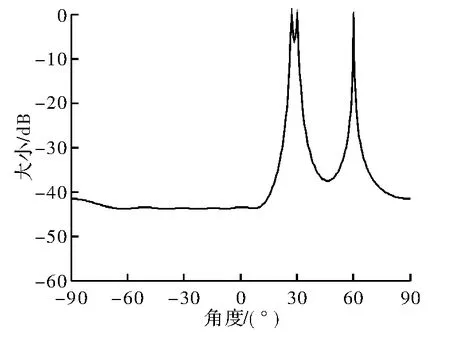
图7 信噪比为10，角度为25°、30°、60°

据仿真结果可知，该种方法可实现良好的DOA估计性能和抗噪声干扰性能，但对角度的分辨率相对较低，即只有信号相差角度大于一定值时该方法才能实现较好地分辨。

5 结束语

通过一种权微扰方法完成了双通道接收机在空间谱估计中实现的理论，经实验论证该方法是正确且有效的。此外空间谱估计技术正在迅速发展，而对于一些理论问题文中仍存在较多的欠缺与不足。由于时间、能力和条件所限，在此只完成了初步的理论设计和仿真实现，并未完成具体的硬件实现过程。

［1］ 赵益民，鞠德航.单通道接收机实施空间谱估计测向［J］.通信学报，1997，18(2):7－11.

［2］ 王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京:清华大学出版社，2004.

［3］ 廖桂生，保铮，张林让.基于特征结构的自适应波束形成器［J］.电子学报，1998，26(3):23－26.

［4］ 张小飞，徐大专.自适应的对角线加载的波束形成算法［J］.中国空间科学技术，2006(2):66－71.

［5］ 刘宁，刘玉生.相干信号的空间谱估计算法研究［J］.计算机仿真，2012，29(11):218－222.