基于脉冲细分法的感应同步器测角方法
周 玮 张 军 王斯琪 朱 凯 徐子立
(中国电力科学研究院武汉分院,武汉 430074)
0 引言
数字测角系统是现代加工定位系统最重要的组成部分之一。感应同步器由于具有耐恶劣环境、能力强、精度高、可靠性好以及价格较低等特点,基于感应同步器的数字测角系统在位置测量领域具有广泛的应用。现代工业领域对测角系统精度提出了越来越高的要求[1]。基于感应同步器的测角系统中应用最多的方法是采用轴角数字转换芯片将感应同步器两相分段绕组输出的正、余弦信号,转换成数字位置信号进行处理。但其轴角数字转换芯片中的积分环节和VCO的线性范围限制了其测量精度,当输入控制电压和跟踪转速提高到某一定值时,会造成很大的转换误差。为简化测量系统,提高测量精度,本文介绍对感应同步器输出信号采用时钟细分的测量方法。
1 时钟细分方法测角原理
以感应同步器励磁信号作为基准信号ui,其波形运动速度为V。设转子运动速度为v,当传感器的转子停止时,感应输出信号u0和基准信号ui都以速度V运动,信号周期为T。设两者在初始t0时刻的相位差为0,u0在t1时刻移动一个节距W,基准信号在t2时刻移动了一个节距W。可以得到如下关系式[2]:
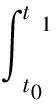
(1)
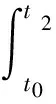
(2)
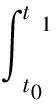
(3)
由式(3)可以看出,通过测量时间差可以求得空间上的位移量。即通过变换,时域信号上的时间差ΔT具有了确定的空间意义。时间差ΔT如果用高频高精度时钟脉冲Pt对其进行细分和计量,则位移变化就可以通过∑Pt的变化来反应,其关系式
(4)
通过时钟脉冲Pt可以求出空间位移量x,再通过高频时钟脉冲对时间差进行细分,其分辨率以及测量精度取决于脉冲细分数多少。
为了便于时钟脉冲细分,需要把感应输出信号u0和基准信号ui分别送入高精度比较器转换成方波信号。根据两路信号上升沿的时间差产生门控信号A,通过对门控信号进行时钟细分计数可测得其对应的开启时间ΔT。设门控信号内时间脉冲计数值为n,信号整周期内计数值为n0,则相位差θx和位移量x分别为
θx=2p ΔT/T=2pn/n0
(5)
(6)
式中,p为感应同步器对极数。设传感器输出信号频率为ω,时钟脉冲频率为ω0,则一个细分脉冲时间Pt对应的位移量Px为
(7)
因此,选取的时钟脉冲频率越高就可以得到越小的分辨率,时钟脉冲细分的测量方法可以比其它方法得到更高的分辨率。采用高速、高精度的FPGA和CPLD芯片能够提供高达数百兆的信号处理速度,能够满足时钟脉冲细分测量的要求。
2 系统设计
基于脉冲细分的感应同步器测角系统主要由转台、励磁电源、信号提取电路、FPGA控制模块、LED显示、串口通信以及PC机构成。激磁电源驱动感应同步器产生电磁感应,转子连续绕组产生与激磁信号相同频率的正弦微弱信号,经过提取电路放大和滤波后把信号变换为方波信号输入FPGA,然后利用时钟脉冲细分方法进行位置测量[3]。测试数据通过串口实时传送到上位机并在LED上显示。测量系统结构如图1所示。
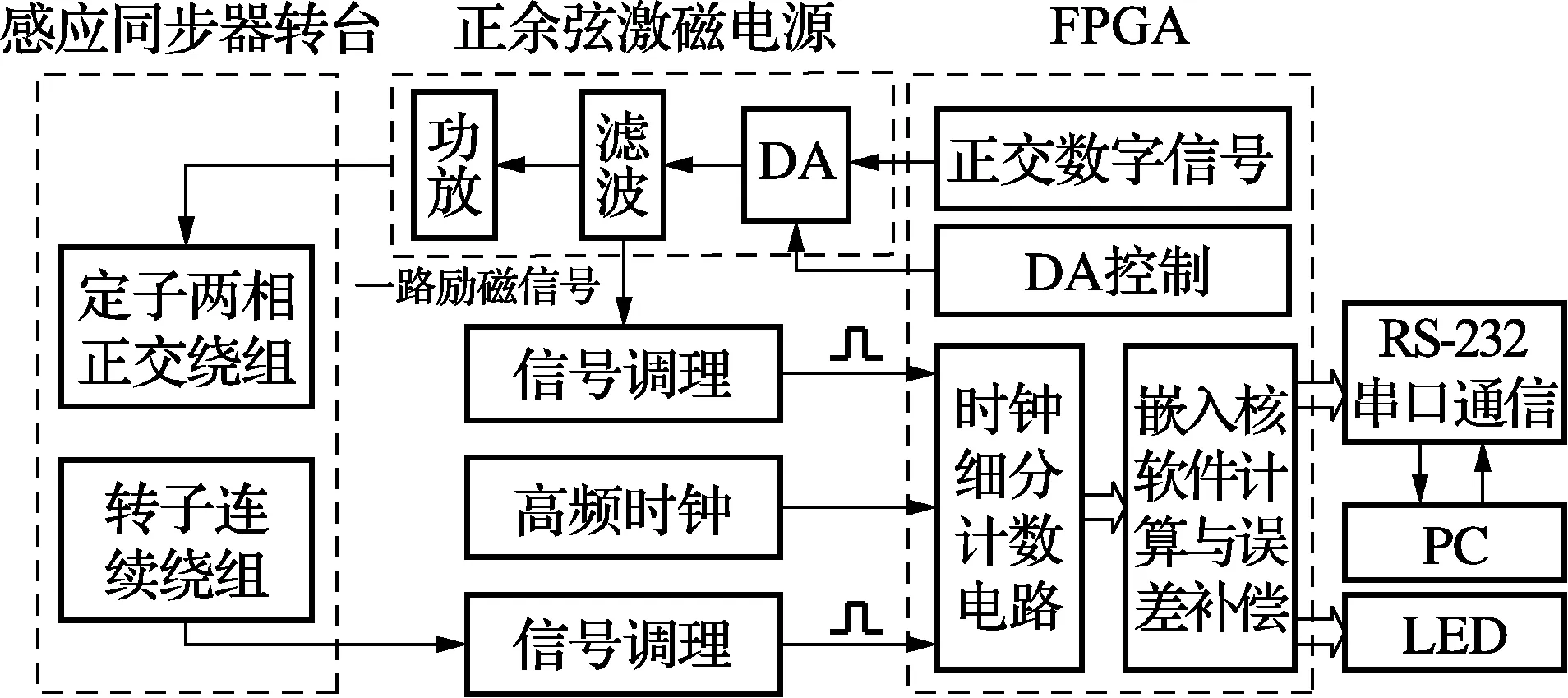
图1 测量系统结构框图
硬件电路主要由FPGA、激磁电源和信号调理电路组成。相比轴角数字转换的方法,系统采用省去了A/D和锁相环环节,结构简单。FPGA选用Altera公司的EP3C10E144C8N芯片,它是一款低成本芯片,具有10320个逻辑单元,2个PLL,423个18×18嵌入式乘法器、10个全局时钟网络,满足系统要求。以FPGA作为控制核心,且这套系统容易实现功能扩展和升级[4]。
2.1 信号调理电路设计
基于时钟脉冲细分方法的角度测量只使用了信号过零点的信息,所以对零电平波动很敏感,很容易受到噪声的干扰[5]。为了得到干净的方波序列信号,采用两片AD8221芯片进行两级差分放大的方式,和高精度过零比较器LM211组成信号调理电路,如图2所示。
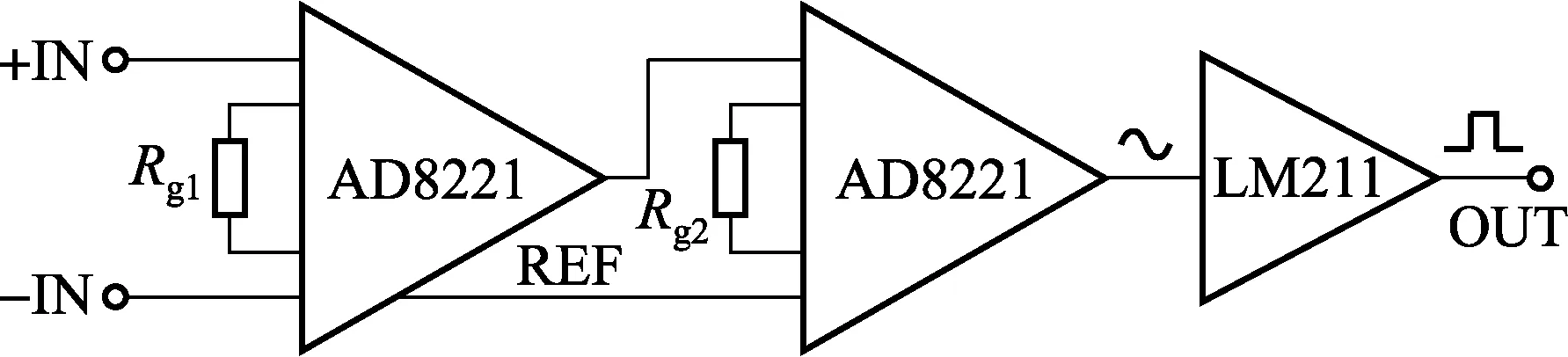
图2 信号调理电路原理
AD8221是一款高性能仪表放大器,具有低电压失调、低失调漂移以及高CMRR特性。差分输入放大方式能够很好抑制共模干扰信号[6],信号调理电路具有一定的抗干扰能力,满足角度测量要求。
2.2 激励电源设计
激磁电源由FPGA正余弦数字波形产生模块、数模转换模块、滤波输出模块和功率放大模块组成。正余弦数字信号是采用DDS技术产生的,能够精确控制信号的波形频率和相位,可以使激磁电源提高稳定性和精度。在当前数字领域中,数字信号发生器的设计多采用这种技术。
2.3 时钟脉冲细分计数电路设计
由式(3)可知,要测量角位移x,需要测量门控信号开启时间ΔT和方波信号整周期时间T。时钟脉冲细分计数电路通过计数器计算ΔT和T时间内的时钟脉冲个数n和n0,然后把计数值送入嵌入式内核。尽管经过信号调理电路的抗噪处理,但是其输出方波信号仍然会产生细微波动,所以对时钟脉冲细分计数电路的设计采用了触发器的边沿触发和锁存功能等措施,具有很高的抗噪能力。
2.4 门控时间计算和辨向
嵌入式内核实时采集时钟计数器数值并计算门控信号开启时间ΔT和方波信号周期T。传感器转子每转过一个节距,信号就会移动一个周期,而计数器在时间ΔT内的计数值n只是一个信号周期内的计数值。当转子正向转动每超过一个节距时,n会发生从最大值向最小值跳变;当其反向转动每超过一个节距时,n会由最小值向最大值跳变。所以在门控时间计算时需要进行辨向设计[7]。ΔT计算和辨向流程图如图3。
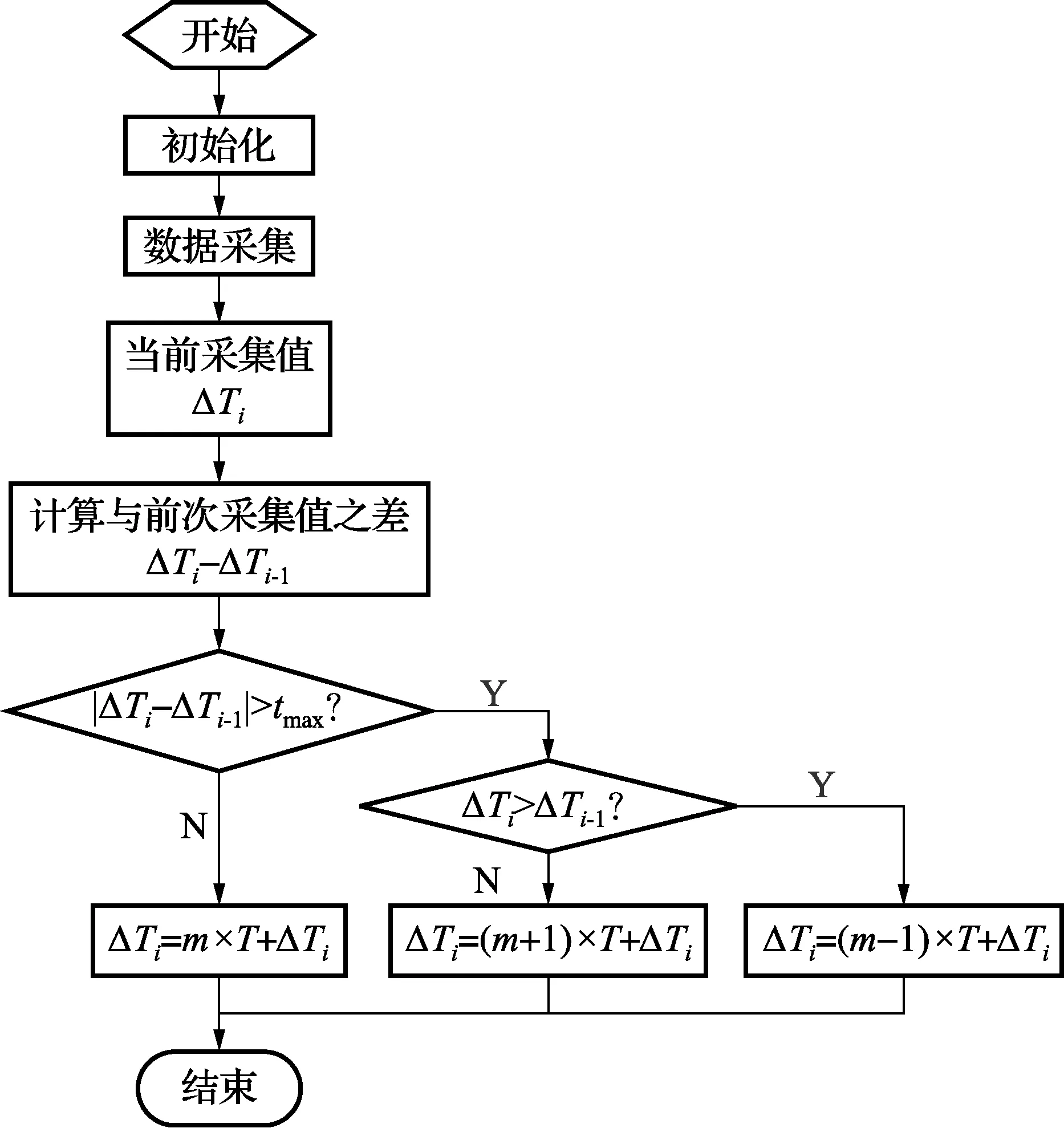
图3 ΔT计算和辨向流程图
其中m为周期数,n0为信号周期内计数值。转子每转动超过一个极距,计数器送入内核的数值会有一个周期的跳变,所以可以通过检测这个跳变进行辨向。
3 实验分析
根据上述思路搭建基于时钟脉冲细分的感应同步器角位移测量系统,配以高精度光栅测角系统进行稳定性实验和精度实验。实验采用的感应同步器为360对极,激磁频率为10kHz,时钟脉冲频率为100GHz,所采用的光栅测角系统精度为±0.5″。
稳定性测试是在一段时间内对传感器在某一固定位置处的测量值进行采集,观察采集的样本值在这段时间内的波动情况。理论上该值是一个定值,但实际上在各种噪声干扰下该值会随时间微小振动。图4为系统稳定性测试曲线,从图中可以看出基于时钟脉冲细分的测角系统稳定性达到±0.6″,满足实际测角要求。在整周范围内测量结果与作为标准器的高精度光栅整周实测数据进行比对,实验结果表明该测角系统示值误差为±3″。
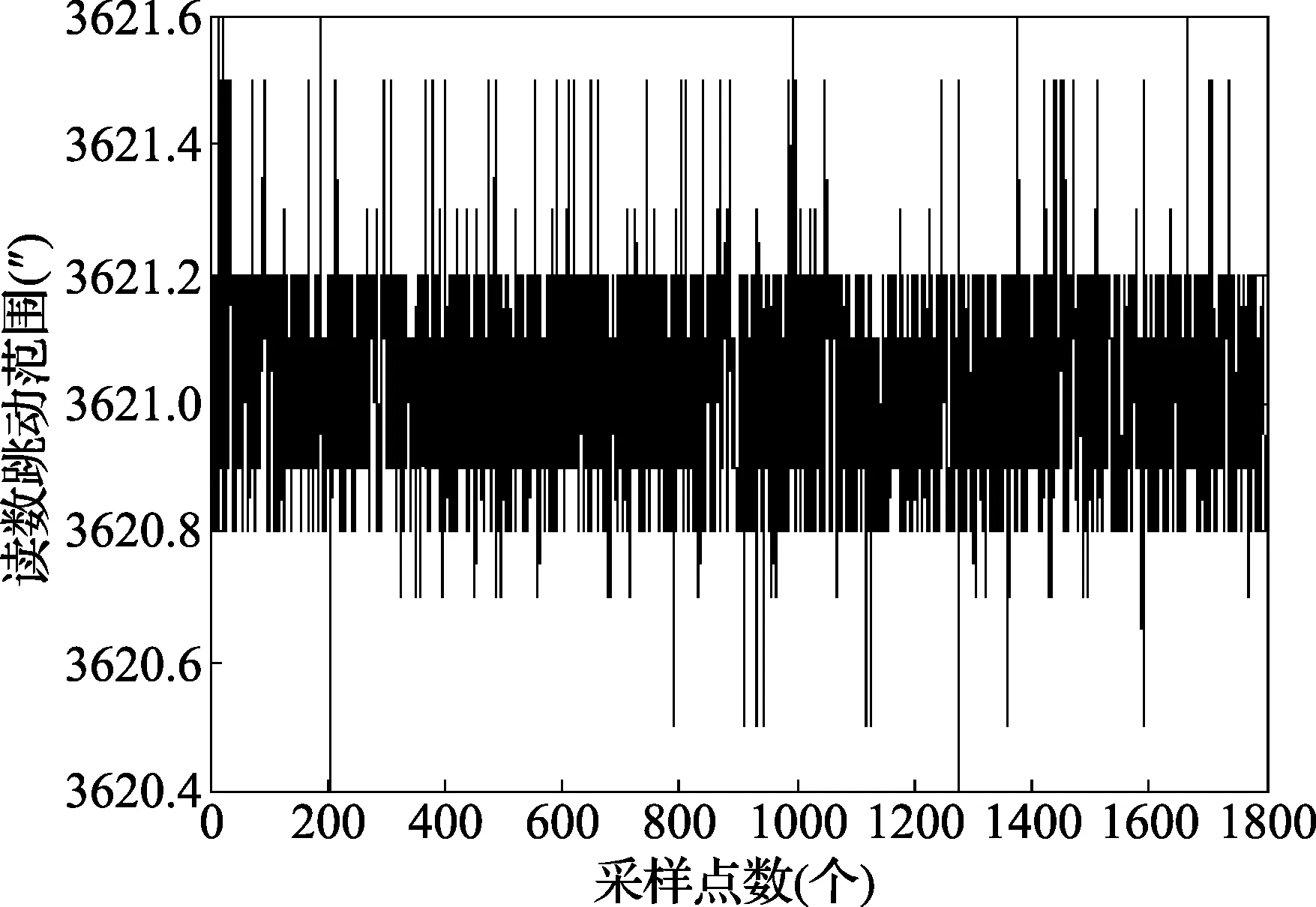
图4 读数稳定性测试
4 结束语
基于脉冲细分的测角方法,采用具有并行信号处理能力的FPGA作为核心处理单元构建了感应同步器的测角系统。该系统基于时钟脉冲细分的测角方法细分数高,省去了A/D和锁相环环节,简化了结构,并有利于系统小型化。通经实验测试,测量系统性能稳定,测量精度为±3″。脉冲细分法对感应同步器测角系统测量精度进一步提高提供借鉴,具有实用价值。
[1] 赵学增.现代传感技术基础及应用.北京:清华大学出版社,2010
[2] 陈锡侯.新型时栅位移传感器研究[学位论文].重庆:重庆大学,2007
[3] Wang Xianquan,Wu Min,Zhu Ge,Feng Jiqin.Detection and Compensation of Amplitude Error and Quadrature Error for Inductosyn.2010 International Conference on Measuring Technology and Mechatronics Automation (ICMTMA 2010),Changsha,2010
[4] 林华安,钱卫飞.基于ARM和FPGA数控信号发生器的设计.计量技术,2011(5)
[5] 王安敏,崔伟,牛传猛.基于AT89C52和AD2S83的圆感应同步器测角系统.仪表技术与传感器,2009,9:55-57
[6] Liu Chengjun,Zou Jibin.Partial element equivalent circuit model of inductosyn.Proceedings of the CSEE.2010,6:018-022
[7] Lou Lina,Zhu Ge,Wang Xianquan,Wu Liang.Error Research and Software Compensation of Inductosyn Angle Measuring System.Computer Measurement & Control.2010,8:1730-1732

