接触式传感器系统中的摩擦颤振研究
张 毅
(北京动力机械研究所,北京 100074)
0 引言
在测量领域,运用了大量高精度的接触式传感器,比如表面粗糙度测量、圆度轮廓测量和三维数据扫描测量等。这些传感器为测量系统采集了大量可靠的数据,因此,传感器稳定、可靠的运行是保证测量任务完成的关键。
笔者在测量某零件过程中,通过比对发现该零件的圆度的实测值经常超出实际值很多,甚至数倍,而且发生的条件也不固定。经过大量的实验,发现接触式传感器的摩擦颤振是误差的来源。进一步研究发现,测针的摩擦速度、角度和测针的选用等都会对实测结果产生影响,而这些因素都是摩擦颤振发生的重要因素[1-2]。
国内外学者对摩擦颤振的研究目前主要集中在机械加工、钻井和机床设备等方面,测量领域摩擦颤振的研究,因为其具有摩擦速度低、结构阻尼小等特点,容易被忽视。笔者通过实验,对接触式传感器摩擦颤振进行研究,为接触式传感器的使用及改进提供依据。
1 实验系统及圆度误差的谐波分析理论
1.1 实验系统
为了分析验证接触式传感器的摩擦颤振现象,笔者选择了TR265型圆柱度及圆度测量仪进行试验。该设备主轴回转精度为±(0.02μm+0.0003Hμm)(H为高度,单位mm);接触式传感器为电感传感器,分辨力为0.012μm;有两种速度可以选择,分别是2r/min(每分钟旋转2圈)、6r/min(每分钟旋转6圈);测针为100、150、200、380mm碳纤维测针(有标准型和测杆加细型两种,测头为人造球形宝石);标准器为玻璃标准半球,精度为0.02μm。
在这个摩擦系统中,摩擦速度、摩擦双方的刚度和阻尼等都是影响摩擦颤振产生的重要因素。实验方案的设计中,选择了两种测量对象:玻璃标准半球体;机加金属外圆柱零件。
本实验以上述两种测量对象的圆度测量为研究对象,通过实验验证接触式传感器的颤振与圆度测量大幅失真是否存在因果关系,并找到消除颤振影响的方法。
1.2 圆度误差的谐波分析理论
圆度测量大幅失真,可表现在圆度误差的颤振谐波分量的振幅加大,所以可以通过圆度误差的谐波分析来研究颤振引起的圆度测量大幅失真现象。圆度误差的谐波分析,是通过线性化处理的方法计算获得被测圆圆心,并经坐标变换得到实际圆轮廓上测点的极坐标,然后应用傅里叶级数展开法分析实际圆轮廓谐波特征。傅里叶定理表明,任何重复的波形可以用各正弦分量之和来表示,因此圆形轮廓由叠加在一起的一系列正弦波组成。
在数据处理过程中,常将工件的圆度误差分布函数r(θ)进行傅里叶变换,提取各次谐波分量。
r(θ)在频域中的复函数模如公式(1)[3]:
(1)
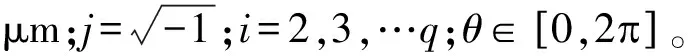
圆度误差的一个显著几何特点是具有“周期性”[4],傅里叶级数中,每转一周的波形构成基本正弦波,其他正弦波都是基本波形的整除空间分量,这些分量可称为n次谐波,即旋转一周有n个周期波,例如:二次谐波是基本谐波除以2,即每转产生两个起伏,有两个周期波。通过圆度误差的谐波数据处理,提取了圆度误差的各次谐波分量,用于工艺诊断和颤振分析。
2 实验分析
2.1 接触式传感器正常谐波分布分析
接触式传感器正常工作时,测针与被测对象之间的摩擦不会产生颤振,传感器采集的是被测对象本身的表面轮廓。对标准玻璃半球进行圆度测量,其输出的谐波分布如图1所示。可见,其谐波只是在低次谐波区域分布。
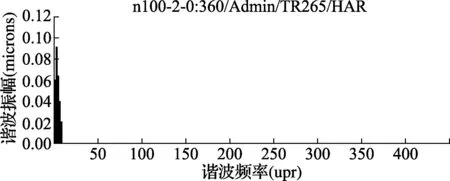
图1 标准玻璃半球正常谐波分布
2.2 颤振发生后的谐波响应分析
对某机加金属外圆柱零件进行圆度测量,圆轮廓示意图如图2所示。
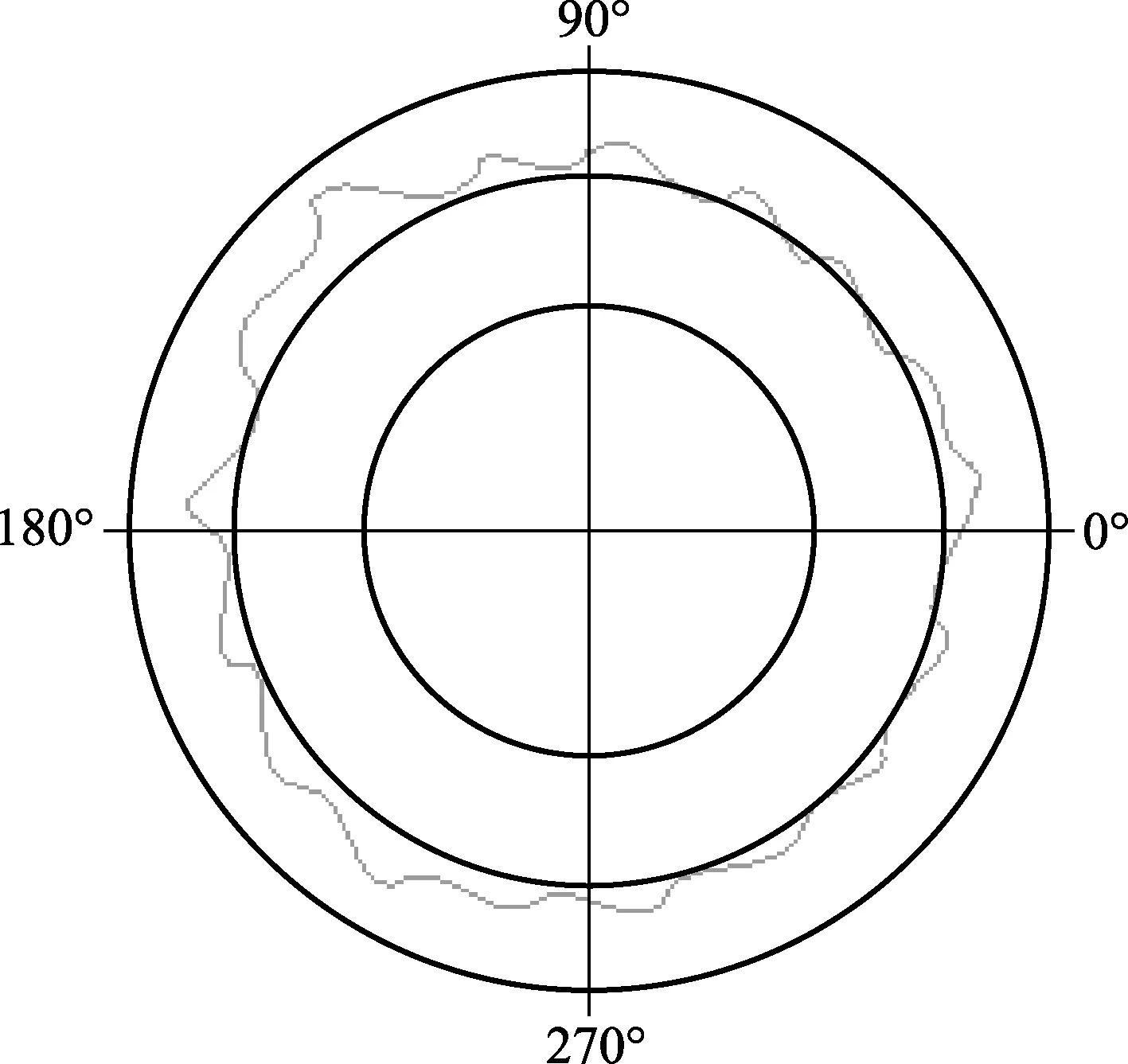
图2 测量某机加金属外圆柱零件的圆轮廓示意图
通过数据分析,接触式传感器发生了明显摩擦颤振,测量该机加金属外圆柱零件输出的谐波响应如图3所示。
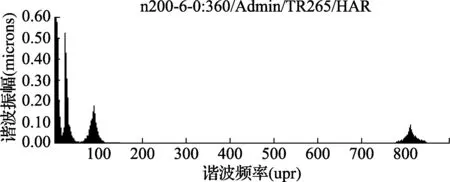
图3 测量某机加金属外圆柱零件发生摩擦颤振谐波分布
由图3可以发现,该机加金属外圆柱的谐波响应,除了在低次谐波区域正常的谐波响应之外,还出现了17次、90 次、812 次谐波响应。要获得正确的测量结果,还需要区分上述3个高次谐波响应中哪些是零件本身的轮廓谐波响应,哪些是传感器摩擦颤振发生的谐波响应。笔者区分响应类型的方法如下:
设计实验方案,采用4种不同的测针、2种不同的转速对该机加金属外圆柱进行圆度测量及谐波响应分析。如果是零件本身的轮廓谐波响应,那么不论选用什么测针和转速,该响应都会发生;如果是摩擦颤振发生的谐波响应,只有在特定条件下才会发生。实验结果如表1。
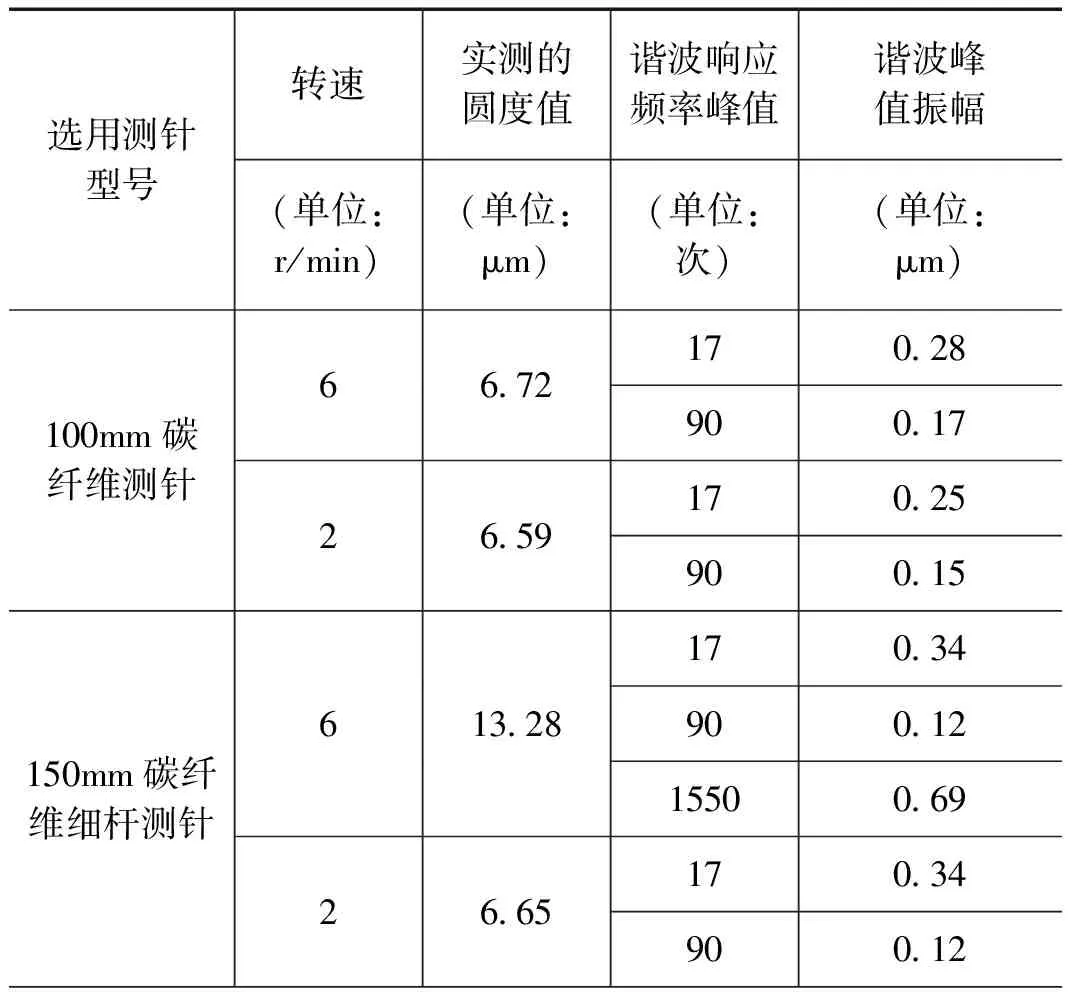
表1 某机加金属外圆柱零件谐波分布实验结果
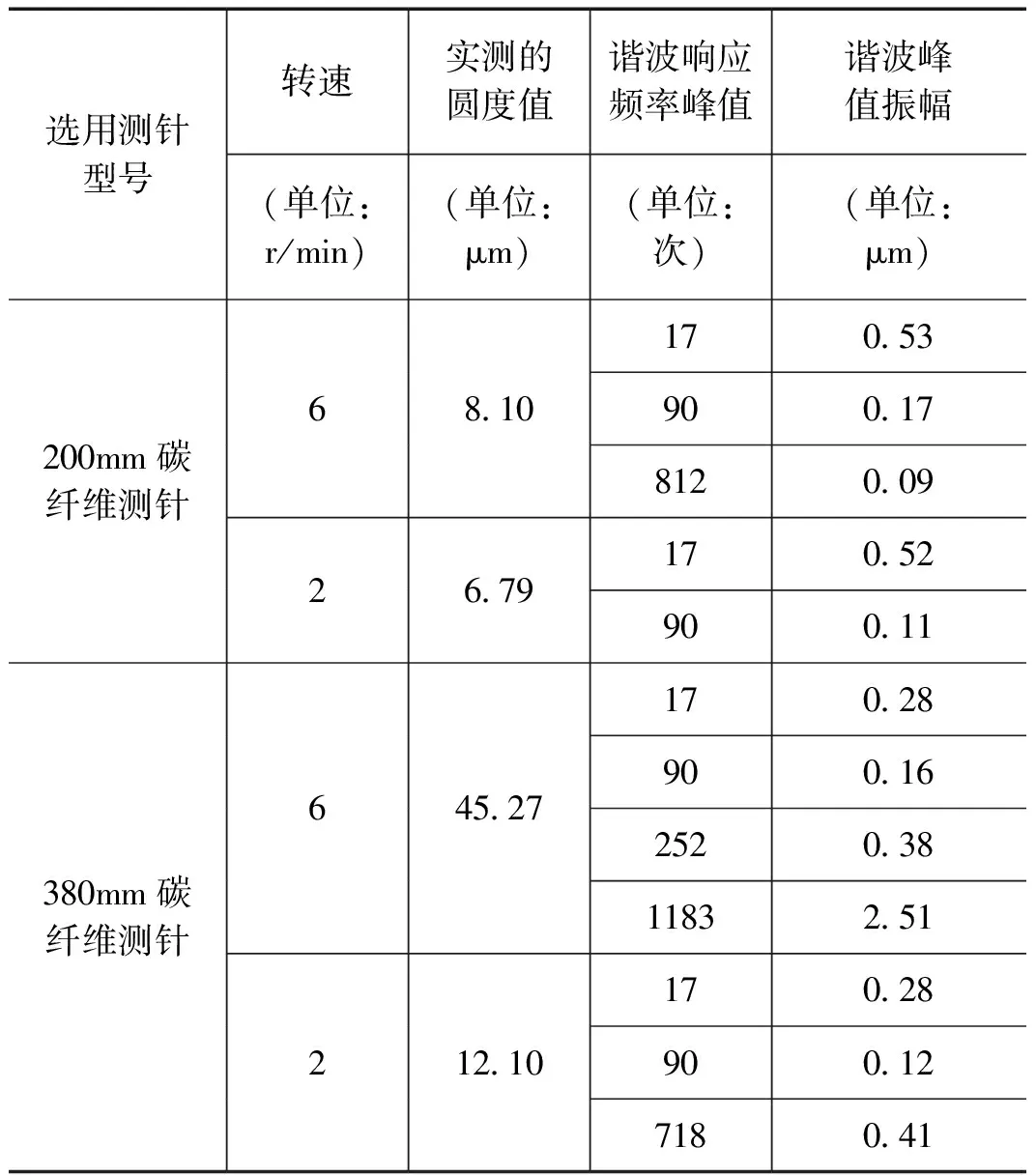
续表
从上述实验结果可以看出,采用4种不同的测针、2种不同的转速对该机加金属外圆柱进行圆度测量及谐波响应分析后,每一次实验都出现了17 次、90 次谐波响应,所以,这两个高次谐波响应可能与零件本身有紧密关联;而其他的高次谐波是传感器摩擦颤振发生的谐波响应。
通过对图2圆轮廓图的较大波形的起伏数的数量的清点[5],可直接得出17次谐波是零件本身的轮廓谐波响应(谐波次数是指一个圆周轮廓每圈产生的周期波的个数);而90次谐波的振幅小,通过图形不能直接得出,它的来源有两种可能:一是来自设备本身的谐波干扰,另一个是来源于该机加金属外圆柱在圆周均布的90条刻线。
为了验证90次谐波不是来自设备本身的谐波干扰,而是零件本身的轮廓谐波响应,笔者又进一步对该零件相同部位的没有刻线的位置进行谐波测量及分析。如果在测量该零件相同部位的没有刻线的位置过程中,没有出现90次谐波响应,则说明这个高次谐波响应不是来自设备本身的谐波干扰,而是来自零件均布的90条刻线。实验结果如表2。
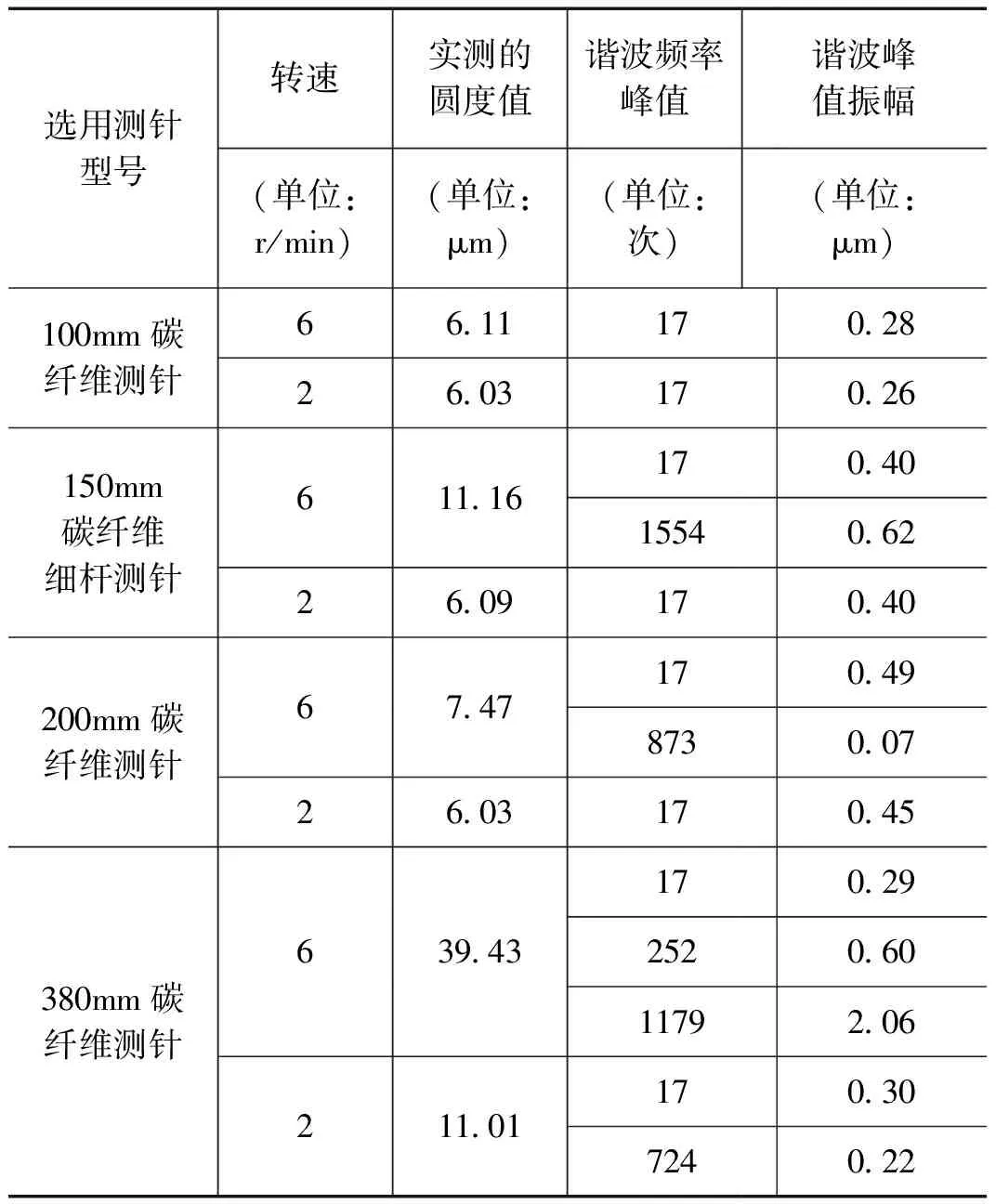
表2 相同部位没有刻线位置的谐波分布实验结果
从上述实验结果可以得出,90 次谐波没有在上述实验中产生,所以,该次谐波不是来自设备本身。
进一步对表1和表2的数据进行综合分析,可以得出以下结论:
1)图3中机加金属外圆柱的谐波响应,除了在低次谐波区域正常的谐波响应外, 17 次、90次是零件本身的轮廓谐波响应,812次是传感器摩擦颤振发生的谐波响应。
2)系统在转速从6r/min降到2r/min情况下,接触式传感器系统的颤振都在不同程度上得到了抑制。
3)如果接触式传感器系统通过摩擦获得足够能量发生了颤振,那么在测量参数相同、测针选用相同和转速相同的情况下,颤振的频率总是在固定频率位置附近出现。
2.3 消除颤振影响的方法
首先是要选择合适的测针。测针本身的刚度和结构阻尼越大,其发生颤振需要的能量越大,颤振越不容易发生。所以要尽量选择刚度和结构阻尼大的测针。测针的长短也是一个因素,接触式传感器的测量方式,绝大部分不符合阿贝原则,测针越长阿贝误差越大。所以要尽量选择短的测针。接触式传感器的测针的制造,也需引入新材料、新工艺来提高测针的刚度和结构阻尼。
其次是要选择合适的摩擦速度。测量领域相对于制造领域,摩擦速度都偏低,所以测量领域的摩擦颤振容易被忽视,但是摩擦颤振一旦发生,对测量结果的影响是很大的。根据对表1和表2的数据进行综合分析,如果在转速6r/min发生了摩擦颤振,可以将转速从6r/min降到2r/min,接触式传感器系统的颤振会在不同程度上得到抑制。
最后是根据谐波响应分布情况,选择正确的滤波范围。如果选择了合适的测针、速度后,还是发生了颤振,就需要根据谐波响应的性质来选择正确的滤波范围。高次谐波响应有轮廓本身的谐波响应和颤振发生的谐波响应两种类型,需要通过多次实验区分响应类型。然后要选择正确的滤波范围。滤波范围有多种,比如1~50upr、 1~150upr和1~500upr(upr为一个圆周轮廓每圈产生的周期波的个数)等,对滤波设置进行改变,能滤掉不同的波形。在图3的试验中,如果设定1~50upr滤波设置,就会把90次轮廓谐波响应(该响应是轮廓本身的有效谐波响应)错误地滤掉,所以应该选择1~500upr滤波设置,只滤掉812次谐波响应,而保留90次谐波响应。选择正确的滤波范围的前提是区分谐波响应类型,然后根据谐波分布选择正确滤波范围。
3 结论
经过实验分析可知,接触式传感器的摩擦颤振,是本文所述的机加金属外圆柱零件的圆度测量结果大幅失真的原因;在滤除传感器摩擦颤振发生的谐波响应时,也要根据谐波响应的类型,选择正确滤波范围。
本文从测量的角度入手,分析抑制颤振的方法,对颤振的发生机理将是有益的验证和补充。在接触式传感器的设计与制造方面,应该提供更广的摩擦速度选择区间、更多的滤波范围组合方式、性能更好的测针等。在航空航天、船舶和机械等领域,研究测量、抑制摩擦颤振的前景是很广阔的。
[1] 黄毅,王太勇,张莹,等.机械系统中摩擦颤振机理的非线性分析.中国机械工程, 2008(7)
[2] 孔祥臻,王勇,蒋守勇,等.基于Stribeck模型的摩擦颤振补偿.机械工程学报,2010(3)
[3] 夏新涛,张青雷,李如强,等.轴承套圈加工表面谐波分布特征研究。 磨床与磨削, 1997(4)
[4] 朱庆保.圆度误差的自适应测评及应用。 计量技术,2000(4)
[5] 张毅.发动机柱形回转体谐波测量及分析.计测技术,2012(2)

