决策树算法在老年性痴呆病因病机分析中的应用

山西中医学院医药管理学院 杨 婕

老年性痴呆，又叫阿尔茨海默病(Alzheimer’s Disease，AD)是一种多发于老年人的神经退行性疾病，临床特征主要有知功能障碍和记忆损害。据报道，老年期痴呆中AD是全世界最致残和最累赘的疾病之一[1]，除了脊髓损伤和晚期癌症以外，AD致残加权显著高于任何其他健康情况[2]，但目前为止AD的早期防治却难以落实。这主要是因为其发病的特殊性，且存在地域性差异，而以往研究又缺乏对AD证候类型、证候诊断的统一标准，所以想要研究AD的病因和发病机制就颇有难度。

如何对AD的中医病因进行科学分类和识别，进而总结提炼归类出可疑痴呆及确诊痴呆各自不同期的中医病机演化规律、致病危险因素以及证候类型的分布规律，已成为AD的有效防治迫切需要解决的问题。

本文的主要工作就是深入研究决策树C5.0算法，并利用太原市迎泽区、万柏林区、杏花岭区三个市区共计1500条数据进行多次实验，根据结果的准确性不断修正算法，最后得到老年性痴呆病因病机的分析模型，用来对太原市人口数据进行患病预测。

1.决策树C5.0算法

决策树（Decision Tree）算法是使用最为广泛的分类预测方法之一，可实现数据内在规律的探究和新数据对象的分类预测。它既可以处理例如“年龄”、“家庭收入”等数值型数据，又很擅长处理如“受教育程度”、“家族遗传史”等非数值型数据，避免了许多数据预处理工作，因此非常适合于研究中医病因分析。

决策树的概念最早出现在CLS(Concept learning system)中，它是由Hunt等人在1996年提出的[3]。现在很多算法都是CLS算法的改进，最经典的算法之一便是C5.0算法。该算法通过计算输入变量的信息增益率确定最佳分组变量和分割点。

将输出变量作为信息源发出的信息U，输入变量看成信宿接收到的一系列信息V。其信息增益为：

Gains( U ,V)=Ent(U)-Ent(U|V)

Ent( U )是平均不确定性：

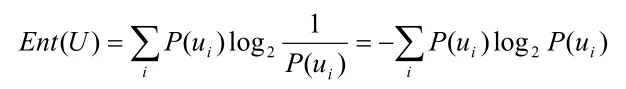
Ent( U |V)是条件熵：

C5.0根据能够带来最大信息增益的字段拆分样本。第一次拆分确定的样本子集随后再根据另一个字段进行拆分，直到样本子集不能再拆分为止。最后检验最低层次的拆分，采用后修剪法从叶节点向上逐层判断错误率，剔除或者修建对没有显著贡献的样本子集。

2.基于决策树C5.0算法的老年性痴呆病因病机预测模型

2.1 数据收集

本文采用流行学的方法在太原市迎泽区、万柏林区、杏花岭区三个市区的医院和社保中心进行调查，收集共计1500条有效信息作为数据集合。其中每条记录由23个字段组成。其中前22个字段是对调研者信息的描述，包括：id、性别、年龄、民族、职业、文化程度、婚姻状况、居住方式、饮食偏嗜、是否饮酒、是否吸烟、是否痴呆、有无脑血管意外、有无帕金森病、有无精神疾患、有无心血管疾病、有无神经系统疾病、有无呼吸系统疾病、有无消化系统疾病、有无内分泌系统疾病、有无血液系统疾病、有无其他系统疾病。最后一个字段是对调研者是否患病的判断，分为：“老年性痴呆(AD)”、“血管性痴呆(VD)”、“混合型痴呆(MD)”和“未患病”四个类别。我们对前22字段进行了分类，如表1所示。

这22个字段是除了id字段，其他都是现代医学的高危因素。在模型建立初期，我们先将其都纳入分析体系中，作为输入变量。

表1 样本字段分类

表2 各样本中患病情况比率

表3 第一层节点各字段信息增益

表4 初次建模分类结果的正确率

表5 初次建模分类结果与字段病型重合矩阵（行表示实际值）

我们对1500条样本记录进行分区处理，随机抽取约80%(1191条)作为训练样本，约20%(309条)作为测试样本。分区后，总样本、训练样本和测试样本中患病情况的分布如表2。

2.2 数据处理

对已采集到的样本数据进行预处理，除噪、除冗余以及连续型属性概化为区间，我们将其储存到计算机之中，得到最终用于建模的样本数据集合。

2.3 初步构建决策树

数据数理完毕后开始构建决策树。首先将输出变量(病型)看成是发出信息的U，共计1191条数据，AD有117条，VD有109条，MD有18条，未患病947条，所以其平均不确定性为

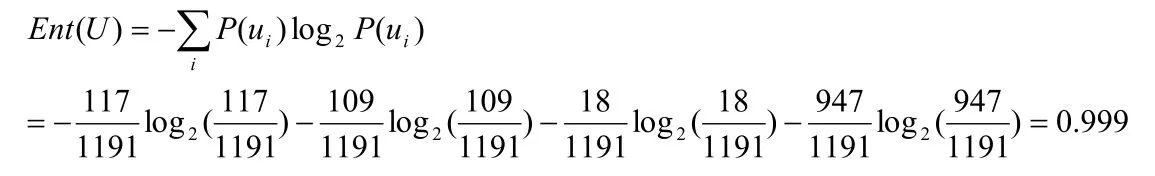
之后分别计算除id之外其他字段的条件熵。以T2（性别）为例，分类有2个，其中男性580条，AD有46条，VD有53条，MD有8条，未患病472条；女性611条，AD有71条，VD有55条，MD有10条，未患病475条，所以条件熵为：

于是T2的信息增益为：

Gains(U,T2)=Ent(U)-Ent(U|T2)=0.999-0.996=0.003

以此类推，分别计算其他20个字段的信息增益，具体信息增益见表3。

发现最大的为饮食偏嗜，说明该字段消除信源的平均不确定性最强，因此选用它作为最佳分组变量。由于该变量为分类型变量，所以按照其取值，分为6组，形成决策树除根节点外的第一层，是一个六叉树。之后重复上面的过程，形成一棵决策树。

决策树构建之后，为了避免该决策树与训练样本的过度拟合，开始对其修剪。修剪方法是从叶节点向上逐层计算节点的真实误差的估计上限ei。

如果叶节点的误差估计大于父节点的误差估计，则剪掉该叶节点。由于数据庞大，在这里我们借助Clementine12.0完成决策树的构建。对初次形成的决策树进行评估分析，具体数据见表4，表5。

从上表的数据可以看出，对已患病的数据错判率较高，为了便于实际中为预防AD的发生，我们通过调整参数对决策树进行修正。

2.4 决策树的修正

为了保证该模型能有效监控AD的发生，我们在误判成本中，考虑尽量避免将AD判为其他取值。

同时为了更好的反应数据规律，减少预测结论的偏差，我们采用Boosting技术对现有训练样本反复抽样以增加样本集。在这里我们迭代了5次，也就是建立了5个模型。之后对这5个模型进行投票，计算其权数的总和。总和最高的就是决策树的最终分类结果。

2.5 最终结果及分析

经过参数修正，我们从5个模型中选取权数和最大(91.27%)的一个模型最为最终结果。对其进行评估分析，得到表6，表7。

从表6和表7中的数据可以看出，最终的模型总正确率和错误率与初次建模的结果基本一致，但是对于患病的判断率明显提高，这符合我们建立模型的初衷。

3.结论

本文介绍了C5.0算法构建决策树的方法，并利用该算法对老年性痴呆建立判断模型，之后用太原市迎泽区、万柏林区、杏花岭区三个市区的医院和社保中心共计1500条数据进行验证。通过剪枝、损失成本矩阵和Boosting技术对得到的模型进行修正，最终得到可信度较高，并具有风险成本低的模型。这说明决策树C5.0算法建立的老年性痴呆判断模型对实际分析具有一定的指导意义，能够为预防老年性痴呆的发生提供决策支持。

表6 最终模型分类结果的正确率

表7最终模型分类结果与字段病型重合矩阵（行表示实际值）

[1]田金洲,时晶,苗迎春等.阿尔茨海默病的流行病学特点及其对公共卫生观念的影响[J].湖北中医学院学报,2009,11(1):3-7.

[2]WorldHealth Organization.WorldHealth Report2003-Shaping the future[J].Geneva:WHO,2003.

[3]季桂树,陈沛玲,宋航.决策树分类算法研究综述[J].科技广场,2007(1):9-12.

[4]郭蕾,王永炎,张俊龙,等.关于证候因素的讨论[J].中国中西医结合杂志,2004,24(7):643-644.

[5]Quinlan J R."C5"[J]-http://rulequest.com 2007.

[6]Rastogi R;Shim K Public:A decision tree classi fi er that integrates building and pruning[J].1998.

[7]张伟,张素贞.粗糙决策树生成方法及应用[C].1999.

[8]石金彦,李旻辰,海燕.基于决策树的数据挖掘方法在故障诊断中的应用[J].水利电力机械,2006,28(4).