短波信道多普勒功率谱密度研究
蒋宇中 刘月亮,2 应文威
(1.海军工程大学电子工程学院,湖北 武汉 430033;2.中国人民解放军海军91269部队,广东 湛江 524088)
引 言
电离层位于地球表面上层大气的导电区域,对于短波通信与高频信号传播起着重要作用[1-3].高频无线电波与电离层相互作用,使由电离层反射的电波发生频率变化,这种变化包括谱线位置的移动和谱线变宽[4],即多普勒频移和多普勒扩展.太阳耀斑爆发、雷电、日出、日落、流星等会使电离层形态随时间变化[4-5],引起经电离层传播的无线电信号的相位路径随时间而变化,从而产生多普勒频移.Davies等人指出了高频多普勒频移与无线电波反射点虚高之间的正比关系[6],Bertel等人给出了无线电波反射点的表观速度与高频多普勒频移之间的关系[7],还有许多学者提供了不同形式的电离层模型下高频多普勒频移的计算公式[8-10].
引起高频多普勒频移的原因很多,其中最重要的是电离层的随机运动,许多文献在此方向展开研究[11-14],多数文献将电离层散射中心的运动建模为单一高斯分布,优点是形式简洁,缺点是无法描述电离层的运动突发变动.本文在文献[5]的电离层模型框架和理论基础上,将电离层的运动假设为正规层与不均匀体两种不同的运动,且每种运动包含整体漂移和随机扰动,其中随机扰动部分进一步建模为二项混合高斯分布,将突发部分的概率和强度以参数的形式加以约定,重新推导了多普勒频移的表达式.在不考虑电子密度随时间变化,并忽略地磁场影响的情况下,推导出了多普勒频移的一种概率密度函数表达式,进而推导出了信号散射分量的功率谱密度函数,实验数据验证了理论推导的正确性.
1 电离层引起的多普勒频移
Bennett假设电离层随时间和空间缓慢变化,忽略电子碰撞的影响,得到多普勒频移的表达式[15]为
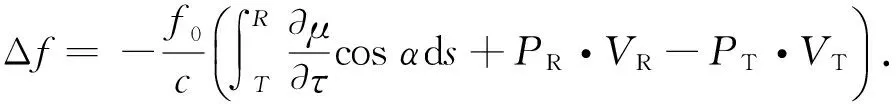
(1)
式中:τ是时间;f0是斜向入射电磁波的频率;c是自由空间中电磁波传播速度; μ为折射指数,是高度和时间的函数;α是波法向与射线方向的夹角,是高度的函数;T和R分别表示发射点和接收点;VT和VR分别是发射机和接收机的速度;PT和PR的数值分别与发、收点的折射指数μT和μR相等,方向均沿着射线方向;积分从发射点到接收点沿射线进行.对于电离层斜向探测而言,发射机和接收机都静止不动(VT=VR=0),多普勒频移的表达式简化为
(2)
为了推导出式(2)的具体形式,对时变电离层作如下假设:
1) 电离层底高度为h0,h0以下折射指数恒为1.
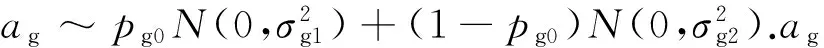
4) 地球磁场是时间的函数,但在所讨论的电离层范围内可以认为与高度无关.
5) 把电离层在水平方向上运动导致的各时刻反射点处电子浓度的不同等效为电离层在水平方向上相对于反射点的位移不同导致的电子浓度的不同(反射点不动),且电子的碰撞效应可以忽略.
6) 接收天线是圆对称的.
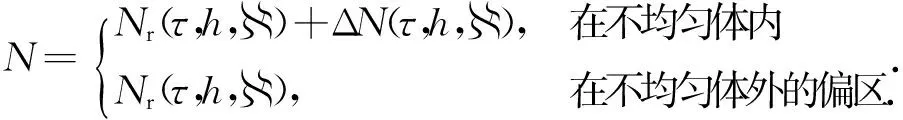
(3)
式中:h是以地面为参考的高度;是电离层以反射点为起点在水平方向上的位移.
采用准纵近似,则可以把电离层的折射指数μ表示为
μ2(τ,h,)
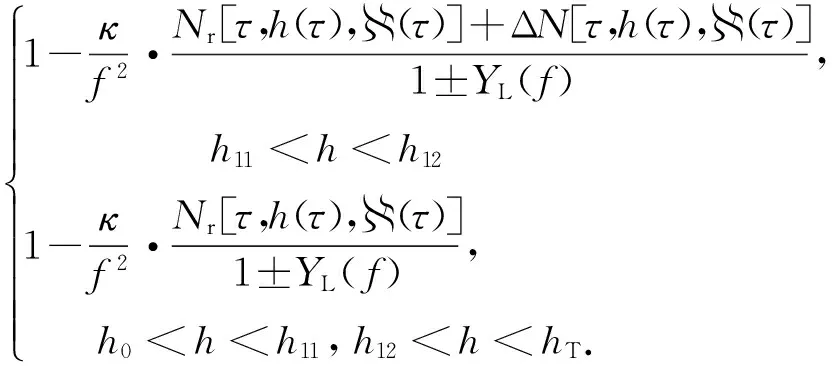
(4)
对式(4)求导,得
(5)
式中:f是频率;κ=80.6;YL=eBL/2πmf,e是电子的电荷,m是电子的质量;BL为地磁场的纵向分量;YL前的正负号分别对应于寻常波和非常波;hT为反射点的高度;h11代表高频信号进入不均匀体的高度;h12是高频信号离开不均匀体的高度.
式(2)中的积分项可以表示为
(6)
式中θ为高频信号在电离层中传播时的入射角,是高度的函数.由假设知
ϑrasinφra)sinβr;
(7)
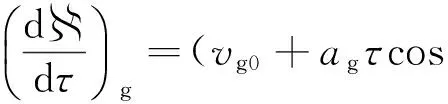
(8)
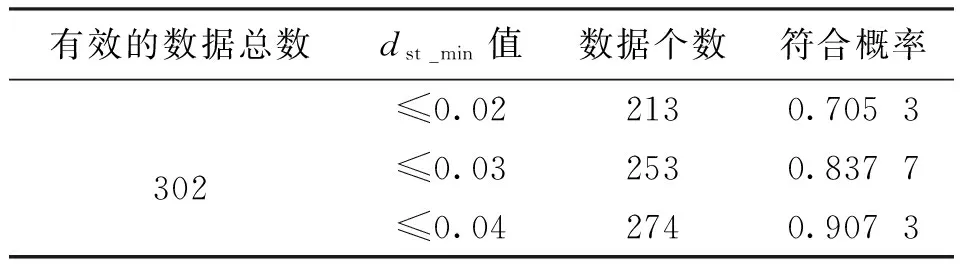
令hr为与正规层一起运动的坐标系中的高度,且hr(τ=0)=h(τ=0),hg为与不均匀体一起运动的坐标系中的高度,且hg(τ=0)=h(τ=0),θ0为高频信号在电离层底时的入射角.对正规层(h0 (9) (10) cosα≈1 ; (11) (12) (13) (14) μcosθ=μ(fv)cosθ0. (15) 式中fv为垂直入射波的频率.对不均匀体(h11 (16) (17) (18) (19) 先计算式(6)的第一项,将式(5)、(10)、(15)代入,可得 2(vr0+arτcos ϑrasinφra)cosβrcosθ0·[μh11(fv)- μh0(fv)]+2(vr0+arτcos ϑrasinφra)sinβrcosθ0· (20) 同理,可得式(6)的第三项为 2(vr0+arτcos ϑrasinφra)cosβrcosθ0· [μhT(fv)-μh12(fv)]+2(vr0+arτcos ϑrasinφra)· (21) 对于式(6)的第二项,将式(5)、(11)、(12)、(15)和(17)~(19)代入,可得 [μh12(fv)-μh11(fv)]+2(vr0+arτcos ϑrasinφra)· (22) 将式(20)~(22)代入式(6),考虑到μhT(fv)=0,并把式(6)代入式(2),可得多普勒频移为 (23) 式中:第一项是电子浓度的时变性引起的多普勒频移;第二项是地磁场随时间的变化引起的多普勒频移;第三、四项是电离层正规层的加速运动引起的多普勒频移;第五、六、七、八项是不均匀体的加速运动与电离层正规层的加速运动的大小与方向不同,以及不均匀体的电子浓度随高度和水平方向而变引起的多普勒频移. 在不考虑电子密度随时间的变化,并忽略地磁场随时间变化的影响的情况下,令 (24) (25) Δfr=η(vr0+arτcos ϑrasinφra), (26) Δfg=ξ(vg0+agτcos ϑgasinφga), (27) 则多普勒频移为 Δf=Δfr+Δfg. (28) 当只考虑正规层的运动时,有 Δf=Δfr=η(vr0+arτcos ϑrasinφra). (29) 根据假设,φra、ϑra和ar的变化相互独立.所以,其联合概率密度函数为 p(ar,φra,ϑra) (30) 令 ρ=φra, (31) V=ϑra, (32) 式(29)、(31)和(32)联立的方程组的解为 (33) 雅可比行列式为 =ητcosϑrasinφra, (34) 则Δfr、ρ、V的联合概率密度函数为 (35) 所以,Δfr的概率密度函数为 (36) 当只考虑不均匀体的运动时,有 Δf=Δfg=ξ(vg0+agτcos ϑgasinφga). (37) 根据假设,φga、ϑga和ag的变化相互独立.所以,其联合概率密度函数为 p(ag,φga,ϑga) =f(ag)p(φga)p(ϑga) (38) 令 ζ=φga, (39) (40) 同理可得,Δfg、ζ、的联合概率密度函数为 p(Δfg,ζ,)= (41) 所以,Δfg的概率密度函数为 (42) 由式(36)知,Δfr服从二项高斯混合分布,即 (43) 由式(42)知,Δfg也服从二项高斯混合分布,即 (44) 假设Δfr与Δfg相互独立,则多普勒频移Δf的概率密度函数为 (45) 由式(45)可知,Δf服从四项高斯混合分布,用f替换Δf,可得多普勒频率的概率密度函数为 (46) 根据第6条假设,可知多普勒频率的概率密度函数p(f)与接收天线所接收的散射分量x(τ)=x1(τ)+ix2(τ)的功率谱密度函数Px(f)成正比[16]. 又因为 (47) (48) (49) 式(49)说明多普勒功率谱密度的形状是混合高斯形的. 对实验所得302个有效的速率为1 000 BD的探测数据进行混合高斯曲线拟合,dst_min值的分布情况见表1.多普勒功率谱密度符合混合高斯形状情况见表2. 表1 dst_min值的分布情况 表2 数据分析结果 从表1和表2可以看出,大部分有效的数据的dst_min的值都小于0.04,小于0.04的概率为0.9073.即使采用0.02作为dst_min值的分位数,dst _min的值小于它的概率仍有0.7053.这充分说明短波信道多普勒功率谱密度如果采用混合高斯分布将有更好的拟合率,证明了理论推导的正确性.本文的研究结果对于指导短波信道仿真器的研发具有重要意义. 短波天波通信主要是靠电离层反射进行的,电离层作为随机变化的介质,其直接影响是使经过电离层传播的高频信号产生频率变化.因此,研究短波电离层信道的多普勒功率谱密度具有重要的意义.本文在假设条件下推导出了短波电离层信道多普勒功率谱密度函数的表达式,并采用寻找误差序列标准差最小值的方法对实际数据得到的多普勒功率谱密度的形状进行了混合高斯形状拟合,拟合结果证明了理论推导的正确性. [1] DHAR A,DAS B N.Propagation of lightning electr-omagnetic pulse(LEMP)through ionosphere[C]∥Proceedings of the 9th International Conference on Electromagnetic Interference and Compatibility,2006,370-373. [2] STEVEN A.Modeling electromagnetic propagation in the earth-ionosphere waveguide[J].IEEE Transactions and antennas and propagations,2000,48(9):1420-1429. [3] 叶志红,廖 成,傅海军.电磁脉冲在电离层中传播特性的分析[J].科学技术与工程,2011,11(19):4449-4452. YE Zhihong,LIAO Cheng,FU Haijun.Analysis of Electromagnetic Pulse Propagation in the Ionosphere[J].Science Technology and Engineering,2011,11(19):4449-4452.(in Chinese) [4] 龙咸灵,侯杰昌.关于电离层反射电波频率变化的问题[J].地球物理学报,1979,22(4):387-395. LONG Xianling,HOU Jiechang.On the frequency variation of radio waves reflected from the ionosphere[J].Chinese Journal of Geophysics,1979,22(4):387-395.(in Chinese) [5] 谢益溪.运动的随时间而变的电离层所引起的多普勒频移[J].地球物理学报,1982,25(4):295-303. XIE Y X.Doppler frequency shifts of radio waves caused by moving and time-varing ionosphere[J].Chinese Journal of Geophysics,1982,25(4):295-303.(in Chinese) [6] DAVIES K,BAKER D M.On frequency variations of ionospherically propagated HF radio signals[J].Radio Science,1966,1(5):545-556. [7] BERTEL L.Multiple-frequency Doppler sounding of the ionosphere[J].Radio Science,1984,19(3):879-890. [8] 黄昌理,乐子华.对“关于电离层反射电波频率变化的问题”一文的意见[J].地球物理学报,1982,25(4):387-390. HUANG Changli,LE Zihua.Comment on the paper“On the frequency variation of radio waves reflected from the ionosphere”[J].Chinese Journal of Geophysics,1982,25(4):387-390.(in Chinese) [9] DAVIES K.Ionospheric Radio Waves[M].New York:Blaisdell Publishing Company,1969. [10] 李 钧.电离层声重波引起的高频多普勒频移[J].地球物理学报,1983,26(1):1-8. LI J.Doppler frequency shifts of a HF radio wave caused by the ionospheric acoustic-gravity waves[J].Chinese Journal of Geophysics,1983,26(1):1-8.(in Chinese) [11] GHERM V E,ZERNOV N N,STRANGEWAYS H J.Investigation into the problem of characterization of the HF ionospheric fluctuating channel of propagation:construction of a physically based HF channel simulator[J].Annals of Geophysics,Supplement,2004,47(2/3):1121-1130. [12] 凡俊梅,焦培南,吴振森,等.电离层不同传播模式信号多普勒频移的实验研究[J].电波科学学报,2008,23(1):35-40. FAN Junmei,JIAO Peinan,WU Zhensen,et al.Experiment research on ionospheric Doppler shift for different propagation[J].Chinese Journal of Radio Science,2008,23(1):35-40.(in Chinese) [13] GUO Y,WANG K.An improved simulation of HF channel with Gaussian random time delays and doppler shifts[C]//Second International Workshop on Cognitive Radio and Advanced Spectrum Management.Aalborg:IEEE Press,2009. [14] SAHAY,S B,BHAGWAT,K C,MOHAN,P R J.Exploitation of MIMO techniques for reliable HF communication[C]//International Conference on Signal Processing and Communications. Pune. IEEE Press,2012. [15] BENNETT J A.Doppler shift formulas for waves in the ionosphere[J].Radio Science,1976,11(7):621-627.
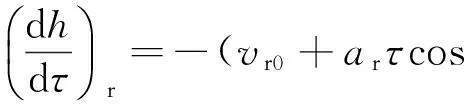
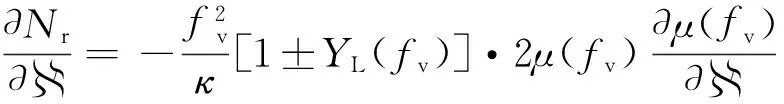

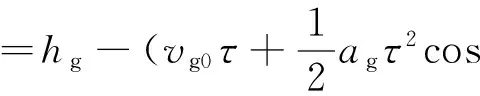
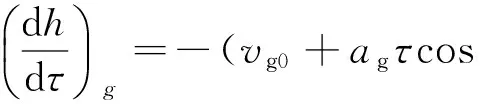
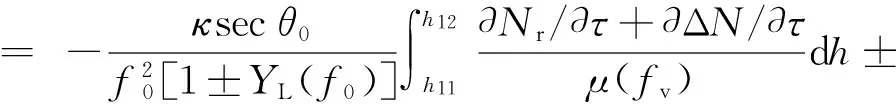

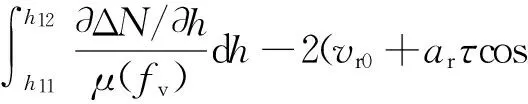
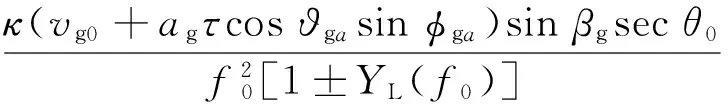
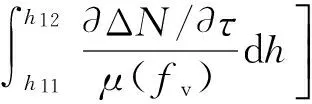
2 多普勒频移的概率密度函数
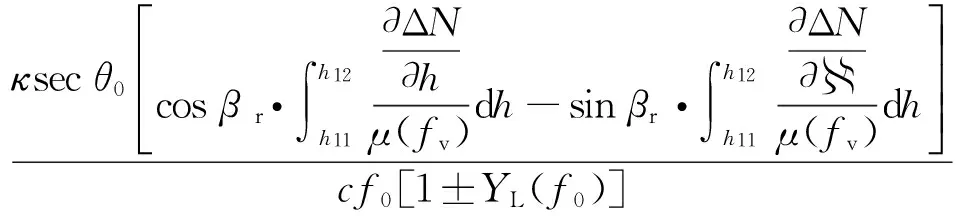
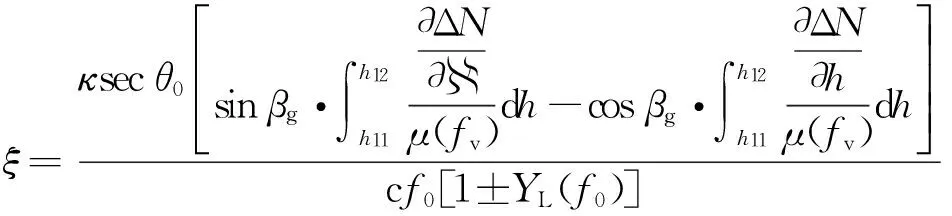
2.1 只考虑正规层的运动时多普勒频移的概率密度函数
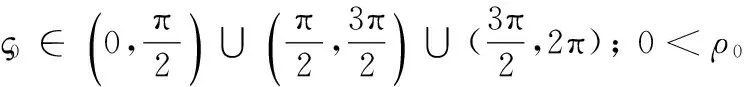
2.2 只考虑不均匀体的运动时多普勒频移的概率密度函数
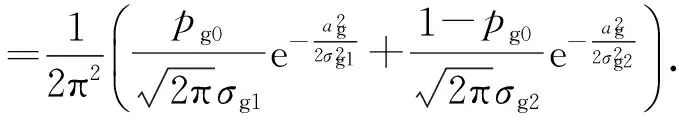
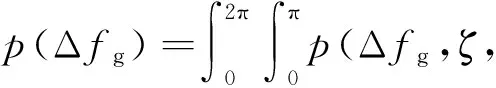
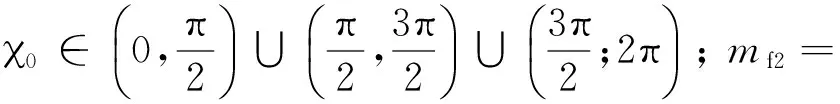
2.3 两种运动都考虑时多普勒频移的概率密度函数
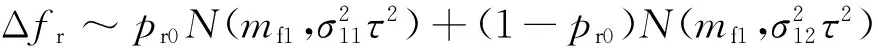
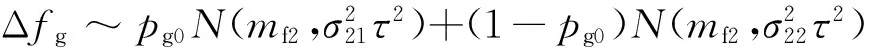

3 多普勒功率谱密度
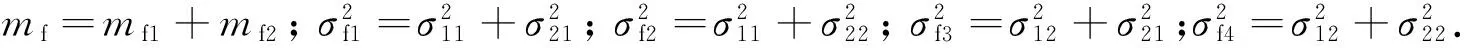
4 对功率谱密度的实验验证


5 结 论

