基于压缩感知的地面运动目标成像方法

顾福飞 张 群 梁 颖 杨 秋 孙凤莲

(空军工程大学信息与导航学院，陕西 西安710077)

引 言

合成孔径雷达(Synthetic Aperture Radar, SAR)可实现全天候、全天时、高增益的地面静止目标成像，具体为通过宽信号频带设计实现距离向高分辨；通过雷达载机平台的运动，等效地在空间形成很长的线性阵列从而实现方位向高分辨[1].然而在很多军事应用情况下，观测场景中不仅存在静止目标，也存在一些运动目标.传统的SAR不具备对运动目标的检测与成像能力，运动目标只能以散焦的形式叠加在静止目标图像上.具有垂直于航向速度分量的动目标在静止目标SAR图像上的方位位置将偏离其真实方位位置，具有沿航向速度分量的动目标在静止目标SAR图像上将出现方位向散焦现象[2].利用SAR获取运动目标检测与成像结果已成为当前军事和民用领域研究热点[3].然而随着SAR精度的不断提高，使得运动目标的回波数据量急剧增加.庞大的数据量对系统的存储能力提出了很高的要求，同时对数据信道的传输能力也是一个很大的挑战.在保证高质量的运动目标成像结果与准确估计运动参数的前提下，如何大幅减少回波数据量对于SAR运动目标成像与检测技术的发展具有十分重要的意义.

考虑到地面静止目标和杂波对消处理后的回波数据中只有运动目标信号，并且观测场景中的运动目标数量是有限的，因此运动目标回波信号满足稀疏性的要求，从而可以采用压缩感知(Compressed Sensing, CS)理论对数据压缩之后的回波信号进行成像和参数估计处理.CS理论是数学家Donoho于2006年提出的一种数据压缩与重建理论[4].近年来，CS理论成为信号处理领域中的一个研究热点[5-8].该理论指出，若信号是稀疏的或在某个变换域稀疏，则可用一个与变换基不相关的观测矩阵将高维信号投影到低维空间，通过求解优化问题即可从低维观测中以高概率重构原信号.可以说CS理论是利用信息采样代替传统的信号采样，这样采样速率不再由信号带宽决定，而是取决于信息在信号中的结构和内容.因此，将CS理论应用于SAR运动目标成像系统，可有效实现对SAR运动目标回波数据的压缩和成像处理.

近年来，分数阶傅里叶变换(Fractional Fourier Transform, FrFT)作为处理非平稳信号，尤其是处理线性调频(Linear Frequency Modulation, LFM)信号的一种强有力的工具，受到广泛的关注[9-12].由于SAR运动目标方位向回波信号可近似为LFM信号，其在时频面上的表示呈斜刀刃状，具有明显的时频特性，因此利用FrFT可实现运动目标的成像与运动参数估计处理[12].但是需要注意的是，由于文章主要针对的是方位向压缩的回波数据，因此利用传统的FrFT处理方法将无法有效实现运动目标成像处理，本文主要通过利用离散的分数阶傅里叶变换矩阵构造稀疏基矩阵，然后再利用压缩感知重构理论获得最终的成像结果，并可根据获得的最优阶数估计运动目标方位向的运动速度和位置信息.

1 理论分析

1.1 回波信号模型

天线结构采用文献[13]给出的单发双收配置方式，即由两个天线通道组成，其中通道A发射信号，通道A和B同时接收回波信号.通道A、B和运动目标的几何关系如图1所示，SAR雷达工作在正侧视模式，O为起始点，雷达载机沿X轴方向飞行，速度为ν，点目标Pn表示场景中的第n个运动目标，其坐标为(xn,Rn) ，垂直于航向和平行于航向的速度分别为 νny和νnx，R0为雷达平台离观测场景中心点的距离，RAn为通道A与Pn的距离，RBn为通道B与Pn的距离，d为通道A和B之间的距离.

图1 通道A、B和运动目标的几何关系图

雷达发射信号为LFM信号，其表达式为

(1)

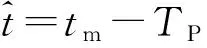
2RAl(tm)/c)2].

(2)

式中：σl是点目标Pl的反射系数；λ为发射信号波长；RAl(tm)为tm时刻通道A与点目标Pl的距离，表达式为

≈RAl-νlytm+[(ν-νlx)tm-d/2-xl]2/(2RAl).

(3)

exp(-j4πRAl(tm)/λ)，

(4)

式中B=γTP为发射信号带宽.根据文献[2]我们知道：通道A和B的回波数据为了能够利用相位中心偏置天线(Displaced Phase Center Antenna, DPCA)方法进行地杂波对消处理，它们之间距离应满足条件d=ε·ν/fPR,ε为整数.利用DPCA方法对距离压缩之后的数据进行对消处理，处理之后的运动目标数据相位信息保持不变.因此，DPCA处理之后的信号可表示为

exp(-j4πRAn(tm)/λ) .

(5)

从公式(5)可见，运动目标的距离徙动包括了线性分量和二次分量，为了讨论问题的方便，暂不考虑二次分量对回波信号的影响.由于数据压缩主要针对方位向数据，因此对于垂直于航向的速度可利用已有的方法进行估计处理，例如文献[14]给出了利用Radon变换估计运动目标垂直于航向的速度，并进行补偿处理的方法，因此这部分不再赘言.令距离向速度为0，这样公式(5)可重新写为

exp(-j4πRAn/λ)·exp{-j2π

[(ν-νlx)tm-d/2-xn]2/(RAnλ)}.

(6)

公式(6)的相位项可简化为关于慢时间tm的LFM信号形式，即

2jπftm+jφ).

(7)

式中：

(8)

(9)

从公式(9)可以看出，经过DPCA处理的地面运动目标回波数据可看作多个LFM信号叠加，由于FrFT对LFM信号具有良好的检测性能，因此下面利用FrFT进行运动目标成像处理与参数估计.

1.2 稀疏性分析

FrFT是传统Fourier变换的推广[15]，信号x(t) 角度为α的FrFT定义为

(10)

式中：p为FrFT的阶数，可以为任意实数；α=pπ/2 ；Fp[·]为FrFT的算子符号；Kα(t,u) 为FrFT的核函数.一个有限长的LFM信号在时频平面上呈现为斜直线的背鳍形分布，而FrFT从本质上讲是对信号的“旋转”，选择合适的旋转角度对信号进行Fourier变换，可使信号在某一特定的分数阶Fourier域上呈现为能量的聚集，其幅度出现明显的峰值.

(11)

假设经搜索得知在旋转角度为α0时得到分数阶域的能量峰值，则回波信号的多普勒调频率和中心频率的估计值为[2]

(12)

(13)

1.3 压缩感知基本理论

对于一个有限长的一维信号H∈RN1，假设其在某规范正交基Ψ={Ψ1,Ψ2,……ΨN1}下可表示为

(14)

式中θn1为投影系数.式(14)写为矩阵形式，即

H=ΨΘ.

(15)

式中：Θ={θn1}为N1×1维的列向量，如果Θ中只有K1个不为零的元素，且K1≪N1，则说明该信号H是K1-稀疏的，Ψ称为稀疏基矩阵.CS理论指出，对于K1-稀疏的信号可用一个大小为M1×N1维的观测矩阵Φ(M1≪N1，M1≥O(K1·lg(N1/K1))[4])对其进行降维观测，得到观测集合U，即

U=Φ·H=Φ·Ψ·Θ.

(16)

显然，观测集合U的元素个数远小于H的元素个数，从而实现了对信号H的压缩采样.从观测集合U重构信号H实际上是一个求解欠定方程组的问题，无法直接求解.CS理论指出，当感知矩阵Φ·Ψ满足约束等距性(Restricted Isometry Property，RIP) 条件时[16]，信号H的稀疏表示Θ可以通过求解最小l0范数问题得到：

Θ=arg min‖Θ‖0s.t.U=Φ·Ψ·Θ.

(17)

对于公式(17)的求解是CS理论中的一个重要内容.当前稀疏重建算法的一种思路是对信号或其变换系数的非零元素个数进行约束，通过0范数最小化求解，代表性的算法是匹配追踪算法和采用连续高斯函数逼近l0范数的平滑l0范数(Smoothedl0, SL0)算法[17]；另一种思路是利用l1范数代替l0范数，将非凸组合优化问题转化为凸松弛问题求解，代表性算法是迭代阈值算法和梯度投影算法.为了兼顾算法的重建精度和效率，在后续的重构处理时采用SL0算法.

1.4 成像与参数估计方法

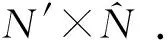
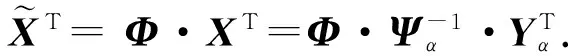
(18)

(19)

由于运动目标的参数信息是未知的，必须通过搜索才能够获得最优的旋转角度.因此，对于不同的旋转角度均需要进行上述公式(19)的求解过程，从而获得对应的Yα，根据第1.2节的讨论得知：当得到的Yα聚焦性能最好的时候，所对应的旋转角度即为最优的旋转角度α0，我们知道熵值最小能量的聚焦性越好，因此选用最小熵法对FrFT变换结果的归一化功率谱进行判决，将熵值最小时对应的旋转角度作为最优的旋转角度估计值.

利用获得的最优旋转角度，并通过公式(12)即可得到运动目标的中心频率参数和调频率参数估计值，再利用公式(8)得到最终的沿航向速度的估计值与方位向位置信息.

2 实验结果分析

为了验证所提方法的可行性和有效性，本部分进行仿真验证并对仿真结果进行分析.雷达正侧视工作，载机的速度ν为150 m/s，载机航线到地面成像中心的距离R0为10 km，发射信号载频f0为10 GHz(波长0.03 m)，脉冲宽度TP为1.2 μs，带宽 B为150 MHz，那么获得的距离向分辨率为1 m.脉冲重复频率fPR为500，成像积累时间为1s，获得的方位向分辨率为1 m.通道A和B的间距d为3 m.假设在观测场景内，有14个静止目标，2个运动目标，反射系数均为1.静止目标随机布置，令运动目标P1的初始位置为 (9 975 m,30 m)运动速度为(0 m/s,20 m/s) ，运动目标P2的初始位置为(10 030 m,0 m) ，运动速度为 (0 m/s,-30 m/s).

首先对接收到的回波数据进行脉压处理，图2(a)为通道A所接收回波在脉压之后的幅度图，可见，通道A的回波信号中同时包含地杂波和运动目标信号，运动目标信息无法分辨开.图2(b)为两通道回波信号进行DPCA杂波对消后进行数据压缩处理，压缩比η为75%得到的回波信号幅度图，图2(c)是对运动目标P1所在的距离单元进行搜索得到的结果，图2(d)是对运动目标P2所在的距离单元进行搜索得到的结果，图2(e)是两个运动目标最终的成像结果，从成像结果可以看出，利用所提方法在大幅压缩回波数据的情况下准确实现了地面运动目标的成像处理.

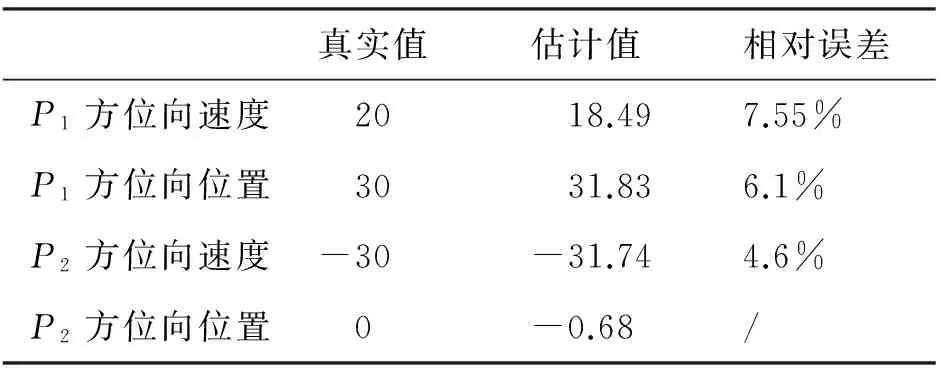
利用上述搜索获得的运动目标的最优阶数，进行运动目标的参数估计.由最优旋转角度α0和u值利用公式(12)可以获得：运动目标1的中心频率为27.43 Hz，方位向信号的调频率为-115.59 Hz2；运动目标2获得的中心频率为2.63 Hz，方位向信号的调频率为-218.64 Hz2.再利用公式(8)求解，获得地面运动目标的运动参数估计，得到的结果如表1所示.从表1可以看出：估计得到的运动目标方位向速度和位置的误差都比较小，估计值比较接近真值，可以对运动目标进行运动状态的描述.

(a) 通道A回波信号幅度

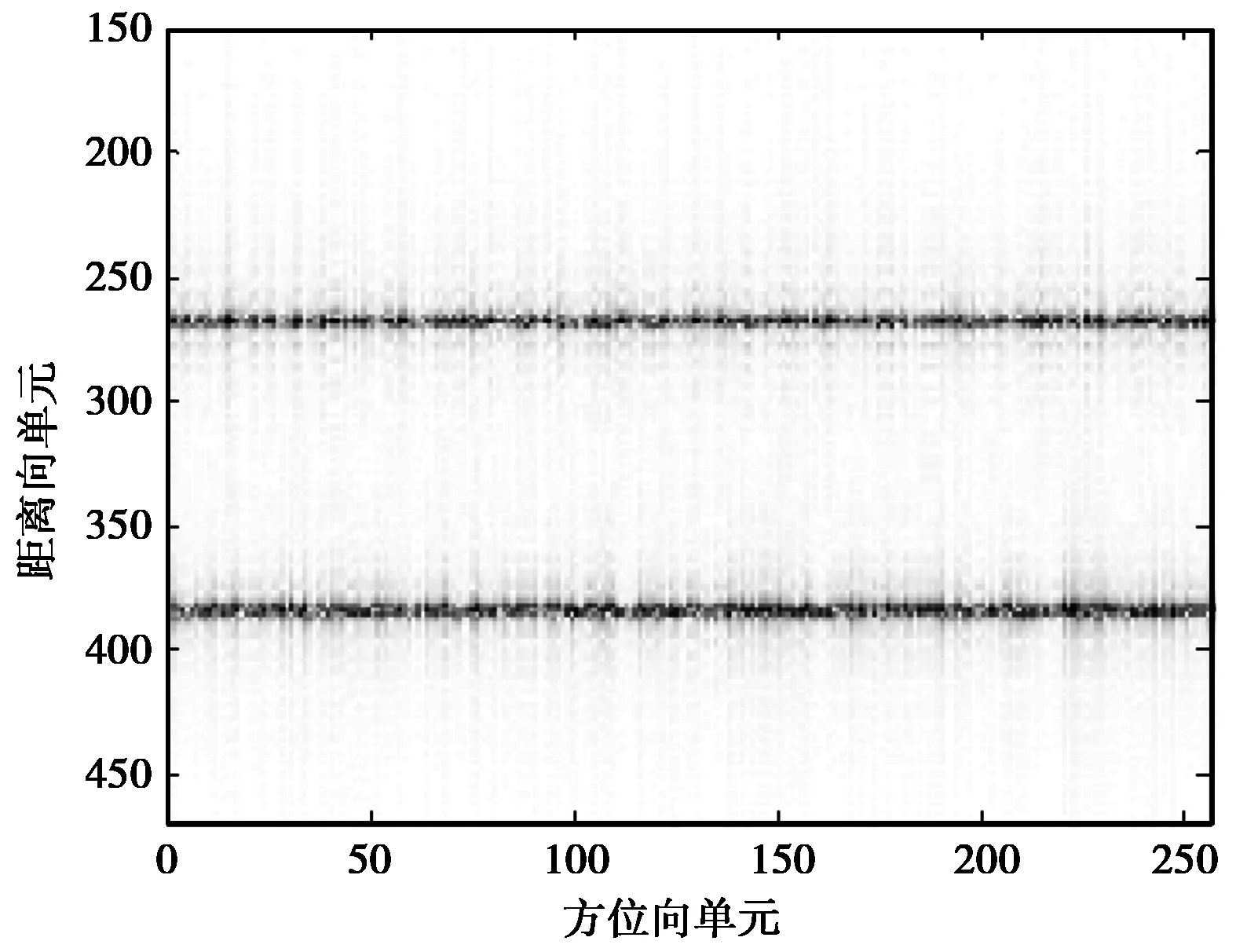
(b) η为75%的运动目标回波数据

(c) P1最优角度搜索

(d) P2最优角度搜索

(e) 最终成像结果图2 η为75%时运动目标成像结果图

真实值估计值相对误差P1方位向速度 20 18.497.55%P1方位向位置 30 31.836.1%P2方位向速度-30-31.744.6%P2方位向位置 0-0.68/

下面分析所提方法在不同信噪比条件下的参数估计性能，回波数据的压缩比η仍然为75%，表2是回波信号的信噪比分别设为10 dB，0 dB，-5 dB情况下的运动目标P1的参数估计结果.可以看出：信噪比大于0 dB时，利用所提方法能够准确估计出目标的运动参数，相对误差不超过10%；当信噪比为-5 dB，由于噪声能量的增强影响了重构的准确度，因此无法获得较为准确的目标运动参数.但总的来看，只要信噪比控制在一定范围之内还是能够得到较为理想的估计结果.

表2 不同信噪比下动目标P1的参数估计结果

3 结 论

针对地面运动目标成像回波数据量较大不便于存储和传输的问题，提出了基于FrFT和压缩感知的成像方法.首先详细分析了双通道回波数据DPCA对消处理方法，其次通过离散分数阶傅里叶变换矩阵构造方法获得稀疏基矩阵，然后利用SL0算法在大幅压缩回波数据的基础上获得了最终的成像结果.仿真结果验证了所提方法能够有效实现对地面运动目标的成像，同时获得的目标运动参数能够准确描述目标的运动状态.

[1] KHWAJA A S, MA J W. Applications of Compressed Sensing for SAR moving-target velocity estimation and image compression [J]. IEEE Trans on Instrumentation and Measurement, 2011, 60(8): 2848-2860.

[2] 孙华东, 宿富林, 高建军, 等. 基于DPCA-FrFT算法的SAR运动目标参数估计 [J]. 吉林大学学报:工学版, 2008, 38(2): 476-482.

SUN Huadong, SU Fulin, GAO Jianjun, et al. Parameter estimation of SAR moving target based on DPCA-FrFT algorithm [J]. Journal of Jilin University Engineering and Technology Edition, 2008, 38(2): 476-482. (in Chinese)

[3] 张 云, 姜义成, 李宏博. 一种改善SAR对舰船目标成像质量的新方法研究[J]. 电波科学学报, 2009, 24(4): 588-592.

ZHANG Yun, JIANG Yicheng, LI Hongbo. Improving synthetic aperture radar imaging of ship targets [J]. Chinese Journal of Radio Science, 2009, 24(4): 588-592. (in Chinese)

[4]DONOHO D L. Compressed sensing [J]. IEEE Trans, on Information Theory， 2006, 52(4): 1289-1306.

[5] BARANIUK R, STEEGHS P. Compressive radar imaging [C]//IEEE Radar Conference, Boston, 2007: 128-133.

[6] 黄 琼, 屈乐乐, 吴秉横, 等. 压缩感知在超宽带雷达成像中的应用[J]. 电波科学学报, 2010, 25(1): 77-82.

HUANG Qiong, QU Lele, WU Bingheng, et al. Compressive sensing for ultra-wide-band radar imaging [J]. Chinese Journal of Radio Science, 2010, 25(1): 77-82. (in Chinese)

[7] BU H X, BAI X, TAO R. Compressed Sensing SAR imaging based on sparse representation in fractional Fourier domain [J]. Sci China Inf Sci, 2012, 55(8): 1789-1800.

[8] 朱 丰, 张 群, 顾福飞, 等. 合成孔径雷达运动目标谱图二维压缩与重构方法[J]. 电波科学学报, 2012, 27(1): 157-164.

ZHU Feng, ZHANG Qun, GU Fufei, et al. Two dimensional synthetic aperture radar moving target spectrogram compressing and reconstructing method [J]. Chinese Journal of Radio Science, 2012, 27(1): 157-164. (in Chinese)

[9] 尹治平, 张冬晨, 王东进, 等. 基于FRFT距离压缩的高速目标ISAR成像[J]. 中国科学技术大学学报, 2009, 39(9): 944-948.

YIN Zhipin, ZHANG Dongchen, WANG Dongjin, et al. Range compression processing based on FRFT for ISAR imaging [J]. Journal of University of Science and Technology of China, 2009, 39(9): 944-948. (in Chinese)

[10]TAO R, ZHANG F., WANG Y. Progress in the discretization of fractional Fourier transform [J]. Sci China Inf Sci, 2008, 38(4): 481-503.

[11] TAO R, LI Y L, WANG Y. Short-time fractional Fourier transform and its applications [J]. IEEE Trans signal process, 2010, 58: 2568-2580.

[12] 邓 彬, 秦玉亮, 王宏强, 等. 一种改进的基于FrFT的SAR运动目标检测与成像方法[J]. 电子与信息学报, 2008, 30(2): 326-330.

DENG Bin, QIN Yuliang, WANG Hongqiang, et al. A modified method of SAR moving target detection and imaging based on fractional fourier transform [J]. Journal of Electronics and Information Technology, 2008, 30(2): 326-330. (in Chinese)

[13] ZHANG W, TONG C M, ZHANG Q, et al. Extraction of vibrationg features with dual-channel fixed receiver bistatic SAR [J]. IEEE Geoscience and Remote Sensing Letters, 2011, 7(3): 450-454.

[14] WU Q S, XING M D, QIU C W, et al. Motion parameter estimation in the SAR system with low PRF sampling [J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 450-454.

[15] 张贤达, 保 铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998: 198-223.

[16] CANDES E. The restricted isometry property and its implications for Compressed Sensing [J]. Comptes Rendus Mathematic, 2006, 246 (9): 589-592.

[17] MOHIMANI G H, BABAIE Z M, JUTTEN C. A fast approach for overcomplete sparse decomposition based on smoothed norm [J]. IEEE Trans on Signal Processing, 2009, 57(1): 289-301.