快速分析雷达散射截面的稻垣模综 合 技 术
王友保 祝 潇
(1.南京信息工程大学江苏省气象传感网技术工程中心,江苏 南京 210044; 2.香港中文大学电子工程系,香港 999077)
引 言
在频域上预测任意形状导体的雷达散射截面,矩量法(Method of Moments,MoM)[1]是一种被广泛采用的有效工具,但MoM只能逐个频点进行计算,其工作效率不高,因此许多科研人员一直在开发电场积分方程MoM的快速求解技术[2-4].另外,特征函数具有一定的物理意义,研究人员常常利用它们对电磁问题进行分析[5-8].
基于在感兴趣的源区域和场区域稻垣模具有正交性和完备性的特点[5],提出了在一个频带上快速预测导体雷达散射截面的稻垣模和广义渐近波形估计(General Asymptotic Waveform Evaluation,GAWE)[9]的混合技术.在这个新技术中,用稻垣模作为基矢构建矩阵方程的解空间,方程的解可通过一组系数将这些基矢组合得到,而这组系数在外推频点通过广义渐近波形估计技术得到.文中给出的几个算例结果表明新算法是有效准确的.
1 理论分析
导体表面的电场积分方程可以写成下列矩阵形式[10]
Z(k)x(k)=v(k),
(1)
式中:Z(k)是已知的阻抗矩阵;v(k)是已知的入射场矢量;k是波数.在求解方程(1)后,可得导体表面电流J为:
(2)
式中:xn是方程(1)中未知量x(k)的第n个分量;N是未知量总数;Fn是RWG (Rao Wilton Glisson)[10]矢量基函数.通过电流J可确定散射电场,从而算出雷达散射截面(Radar Cross Section,RCS).
1.1 稻垣模
方程(1)可以变形为
Z(k)HZ(k)x(k)=Z(k)Hv(k),
(3)
式中:Z(k)H是Z(k)的伴随算子,上标H表示矩阵的共轭和转置.算子Z(k)HZ(k)是厄密特(Hermitian)算子,令M(k)=Z(k)HZ(k),可选取电流gi满足下列方程
M(k)gi=λigi,
(4)
式中:M(k)为特征值方程;λi是特征值;gi是特征函数(又称稻垣模).厄密特算子M(k)的特性确保了特征值是实的且是半正定的,特征函数在源区是正交完备的[5],因此方程(3)的解可写为
(5)

在给定频点k0处,解空间G(k)的基矢(稻垣模)gi(k)可以写为[11]
gi(k)=gi(k0)+Vci(k)gi(k0),
i=1,2,…,N,
(6)
式中Vci(k)是k的函数.将式(6)代人式(5),可得
=G(k0)s(k)
(7)
式中
s(k)=[c1(1+Vc1(k)),c2(1+Vc2(k)),
…,cN(1+VcN(k))]T.
因此,在得到k0处的解空间G(k0)后,通过系数矢量s(k)可以得到方程(1)的解.
1.2 GAWE技术
将式(7)代入方程(1)有
Z′(k)s(k)=v(k),
(8)
式中,Z′(k)=Z(k)G(k0),求解方程(1)中x(k)的问题就转化为求解方程(8)中的s(k).根据GAWE技术[9],在k0附近,方程(8)的解s(k)可以表示如下
(9)
式中:b0是每个分量均为1的N维列矢量;a0,a1,…,aL和b1,…,bM均为N维列矢量,并且由GAWE技术确定.详细求解过程参见文献[9].另外,对于一个固定的导数阶数L+M,当取L=M或L=M+1时,误差是最小的[12].一旦求得s(k),通过式(8)就给出了x(k),从而根据式(2)就可以给出导体表面的电流分布,进而每个频点的RCS就可以被确定了.
2 数值分析
本节算例均以频率步长为0.1 GHz,分别对6阶导数(L=3,M=3)和8阶导数(L=4,M=4)情况下的单站后向RCS的频率响应进行计算.入射平面波电场E的极化方向设定为y轴方向,传播方向设定为k,相应磁场H的极化方向沿y轴方向,入射波均画在相应算例频率响应图中.为了比较,同时给出了通常的外推技术渐近波形估计(Asymptotic Waveform Evaluation,AWE)的结果和矩量法方法的结果.所有的计算都是在同一台计算机上进行的.该计算机配置为Dell Sever PE6800,Intel(R) Xeon(TM),3.00 GHz, 2.99 GHz ,31.9 GB of RAM.
2.1 算例1
将中心有一半径为0.7 cm圆孔的方导体板(2 cm×2 cm)离散成712个小三角区域,这样便有1 004个未知电流系数.展开频点选在15 GHz,研究的频率范围为10~20 GHz.对于6阶导数、8阶导数情况的运算,新技术计算耗时为203 s和297 s、 AWE技术计算耗时为188 s和280 s, MoM方法计算耗时为995 s.显然,用新技术、AWE技术预测RCS的计算速度要比MoM方法快得多.这是因为MoM方法中,每个频点均需求解矩阵方程,得到电流分布后,再算出RCS;而在AWE方法中,只需在展开频点解矩阵方程,得到匹配系数,进而求得各个频点的电流分布及RCS;类似地,在新方法中,也只需在展开频点解矩阵方程,得到作为解空间基矢的稻垣模和匹配系数,进而求得各个频点的电流分布及RCS.由此可见,MoM方法因多次求解矩阵方程,求矩阵逆的过程中要花费大量时间,所以,在预测一定频率范围的RCS时,MoM方法比AWE技术、新技术运算均要慢得多.另外,新技术与传统AWE技术相比,在同阶导数情况下,运算速度略慢,但外推频率范围更大(参见图1).造成上述情况的原因是在新技术中需要计算展开频点处的稻垣模,从而比AWE技术多花一些时间;至于新技术展开频率范围更大的原因在于稻垣模是根据矩阵方程中的阻抗矩阵求得的,阻抗矩阵元素与散射物的几何特性有关,也就是说,稻垣模带有散射物的几何特征信息,由此导致新技术比AWE技术外推频率范围更大.从图1也可看出,用新技术进行频率外推是有效的.

图1 带孔方板的单站RCS频率响应
2.2 算例2
考虑一个由两块1 cm×1 cm导体方板组成的60°角板的散射情况.将该角板表面剖分为632个三角形子区域,相应有918个电流未知系数.频率展开点选在25 GHz,研究的频率范围为15~40 GHz.对于6阶导数、8阶导数情况的运算,新技术计算耗时为155 s和 225 s、 AWE技术计算耗时为141 s和 207 s, MoM方法计算耗时为1 739 s.数值结果参见图2,该算例所得结论类似带孔导体方板算例1的结论.
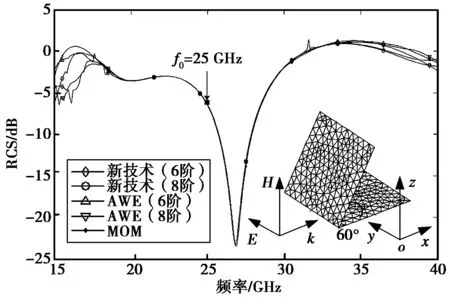
图2 角板的单站RCS频率响应
2.3 算例3
分析一个1 cm×1 cm×1 cm立方导体的散射情况.将该立方导体表面剖分为588个三角形子区域,相应有882个电流未知系数.频率展开点选在15 GHz,研究的频率范围为2~30 GHz.对于6阶导数、8阶导数情况的运算,新技术计算耗时为131 s和 186 s、 AWE技术计算耗时为121 s和 171 s, MoM方法计算耗时为1 155 s.数值结果参见图3,该算例所得结论类似上述两个算例的结论.
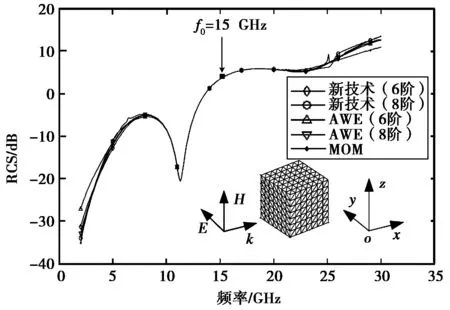
图3 立方体的单站RCS频率响应
3 结 论
提出了将稻垣模与GAWE技术相结合的快速分析任意形状导体RCS的综合技术.从所给的算例来看,新技术是一个有效、准确的算法.另外,需特别强调的是虽然数值最终结果给出的是RCS的频率外推,但实际上在此之前,首先要进行稻垣模的频率外推,这就暗示了带有一定物理意义的稻垣模分析其他电磁问题时也将会有所帮助.
[1] HARRINGTON R F. Matrix methods for field problems [J]. IEEE Proceedings, 1967, 55(2): 136-149.
[2] TANG T K, NAKHLA M S, GRIFFITH R. Analysis of lossy multiconductor transmission llines using the asymptotic waveform evaluation technique[J]. IEEE Trans Microwave Theory and Techniques, 1991, 39(12): 2107-2116.
[3] COCKRELL C R, BECK F B. Asymptotic waveform evaluation(AWE) technique for frequency domain electromagnetic analysis[R]. NASA Technique Memo 110292, 1996.
[4] 姬伟杰, 童创明. 二维海面上方金属目标复合散射快速算法研究[J]. 电波科学学报, 2012, 27(2): 307-314.
JI Weijie, TONG Chuangming. Fast Algorithm of Calculating the composite scattering from PEC object above sea surface[J]. Chinese Journal of Radio Science, 2012, 27 (2): 307-314. (in Chinese)
[5] INAGAKI N, GARBACZ R J. Eigenfunctions of composite hermitian operators with application to discrete and continuous radiating systems[J]. IEEE Transactions on Antennas and Propagation. 1982, 30(4): 571-575.
[6] HARRINGTON R F, MAUTZ J R. Computation of characteristic modes for conducting bodies[J]. IEEE Transactions on Antennas and Propagation, 1971, 19(5): 629-639.
[7] 叶红霞, 金亚秋. 二维密集导体目标散射的数值模式匹配法[J]. 电波科学学报, 2010, 25(2): 203-208.
YE Hongxia, JIN Yaqiu. Numerical mode match method for scattering computation of densely distributed 2D PEC targets[J]. Chinese Journal of Radio Science, 2010, 25(2): 203-208. (in Chinese)
[8] 李志平. 双站散射模式响应的分析与应用[J]. 电波科学学报,2011, 26(2): 222-225.
LI Zhiping. Bistatic model scattering response an analysis and its application[J]. Chinese Journal of Radio Science, 2011, 26 (2): 222-225. (in Chinese)
[9] WANG Y B, BO Y M, BEN D. Fast RCS computation with general asymptotic waveform evaluation[J]. Journal of Electromagnetic Waves and Applications, 2007, 21(13): 1873-1884.
[10] RAO S M, WILTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(3): 409-418.
[11] WANG Y B, BO Y M, JI G Q, et al. Hybrid technique of fast RCS computation with characteristic modes and AWE[J]. IEEE Antennas and Wireless Propagation Letters, 2007, 6(11): 464-467.
[12] FELDMANN P, FREUND R W. Efficient linear circuit analysis by Padé approximation via the Lanczos process [J]. IEEE Transactions on Computer-aided Design, 1995, 14(5): 639-649.

