辐射目标被动探测的阵列信号反演算法研究
徐玉清 周新建 沈晓强
(总装工程兵科研一所,江苏 无锡 214035)
引 言
辐射目标被动探测是利用目标自身辐射或者反射的电磁波进行探测的方法,是微波遥感与探测的重要方面.辐射被动探测的主要手段是微波辐射计,但传统辐射计受天线波束限制导致空间分辨率很大,无法满足实际需要.20世纪80年代末发展起来的综合孔径微波辐射计引入射电天文学“孔径综合”的思想,通过阵列稀疏、相关接收等技术,有效解决了传统微波辐射计口径有限、机械扫描困难等问题,极大提高了观测的空间分辨率,因而成为近年来微波被动遥感的一个重要发展方向[1-3].但综合孔径技术本质上属于空域傅里叶变换,其分辨率同样受限于傅里叶限,即阵列波束范围内的目标无法分辨.另外,随着综合孔径阵列增大,接收天线有效面积减少,导致接收信噪比随之降低.当分辨率达到一定程度时,会与系统灵敏度产生矛盾,导致分辨率不能无限增加.这需要研究新的算法,以进一步提高被动探测的系统空间分辨率,满足实际需要.
阵列信号处理是信号处理领域一个重要分支,其利用空间不同位置的传感器阵列对空域信号进行多点并行采样和处理,提取阵列所接收的信号及其特征信息,同时抑制干扰和噪声.阵列信号处理具有灵活的波束控制、高的信号增益、极强的抗干扰能力和高的空间分辨率等优点.阵列信号处理主要研究方向包括空间谱估计和自适应空域滤波.空间谱估计主要是指空间信号的波达方向(Direction of Arrival,DOA)估计,在电子侦察、智能天线、雷达、声纳等领域具有广泛的应用[4-9].传统的空间谱估计方法的分辨率受限于阵列的角度分辨力,即阵列的物理孔径限,常称为“瑞利(Rayleigh)限”,对于一个波束宽度内的空间目标不可分辨.因此提高空间分辨力只能扩展阵列的物理口径,这在很多情况下不可实现.从20世纪70年代末,以美国Schmidt R.O.等人提出的多重信号分类方法(Multiple Signal Classification, MUSIC)为代表,标志着空间谱估计方法向现代超分辨测向技术的飞跃[7,9].MUSIC算法能实现波束范围内目标DOA的超分辨估计,因此具有极大的应用价值.MUSIC算法的提出也促进了特征子空间(或称子空间分解)类算法的兴起[5].
辐射目标被动探测中引入空间谱估计算法,可以突破空域傅里叶限,在一个波束内实现超分辨探测.相比综合孔径阵列,空域减少阵列孔径,增加接收面积从而降低噪声,不会与系统灵敏度产生矛盾.因此在辐射目标被动探测中具有重要的理论和实用价值[10].本文基于阵列信号处理中的空间谱估计算法,建立了辐射目标亮温反演模型,从阵列接收数据的协方差矩阵推导得到了辐射目标信号信息,同时完成辐射目标方位和功率的估计.通过仿真与实验,阵列信号算法具有超越综合孔径的高分辨率,并且阵列接收结构更加简单.
1 物理模型

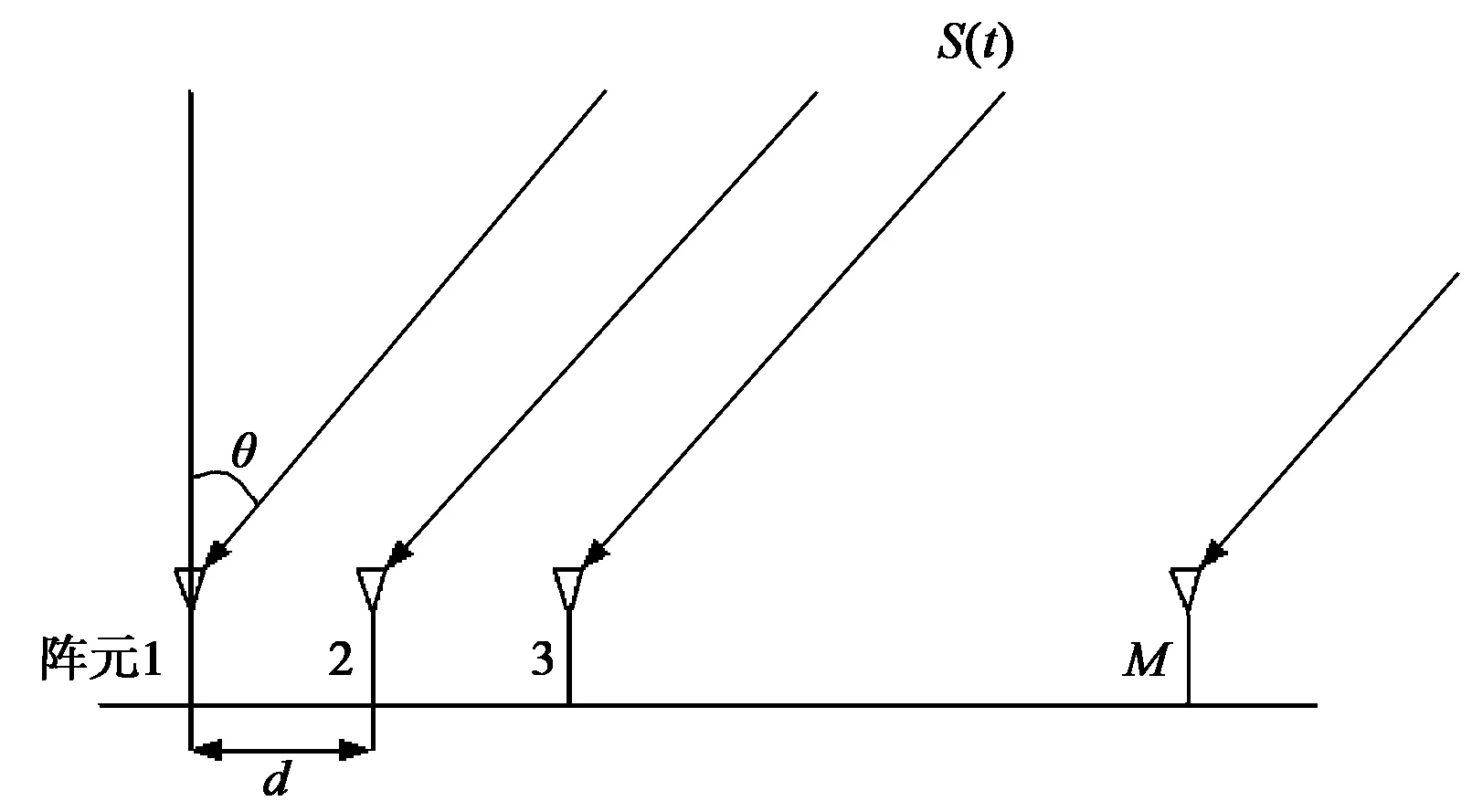
图1 阵列信号接收示意图
由于信号到达各个阵元有时间延迟τ,则单个信号可以如下表述:
(1)
式中:ui(t)为第i个信号的幅度;φ(t)为信号的相位;ω0为信号接收的频率.在窄带信号且远场信号源的假设下,有如下近似[5]:
(2)
显然有
si(t-τ)≈si(t)e-jω0τ,i=1, 2, …,N.
(3)
则第l个阵元接收的信号为
l=1,2,…,M.
(4)
式中:gli为第l个阵元对第i个信号的增益;nl(t)表示第l个阵元接收通道的噪声;τli表示第i个信号到达第l个阵元时相对于参考阵元的时延.
在理想情况下,假设阵列中各个阵元是各项同性的(即方向图为理想方向图),各通道不存在不一致、互耦等误差因素的影响.因此式(4)中增益可以省略(归一化为1).在此假设下,式(4)写为矩阵形式:
(5)
将式(5)写为如下矢量形式
X(t)=AS(t)+N(t) .
(6)
式中:X(t)为M×1维阵列接收数据矢量;N(t)为阵列的M×1维噪声数据矢量;S(t)为空间信号的N×1维矢量;A为空间阵列的M×N维流型矩阵(导向矢量阵).
A=[a1(θ1)a2(θ2) …aN(θN)] .
(7)
ai为第i个入射信号对应的导向矢量,其入射角为θi.
针对间距为d的一维均匀线阵,假设信号以方向角θi入射到阵列,则到达相邻两阵元的时间差为
τ=dsinθi/c.
(8)
由ω0=2πf=2πc/λ,则导向矢量
(9)
由式(9)可以看出,信号的时延中包含信号的入射角信息,空间谱估计理论的基本思想就是利用信号导向矢量来估计其空间入射角θi[6-7].
对于式(6)描述的数学模型,考察阵列快拍数据的协方差矩阵
R=E{XXH}=AE{SSH}AH+E{NNH}
=ARSAH+RN.
(10)
式中RS与RN分别为信号协方差矩阵以及噪声协方差矩阵.对于空间理想的白噪声,且噪声功率为σ2,有下式成立:
R=ARSAH+σ2I.
(11)

(12)
式中L为接收数据长度,即快拍数.
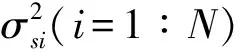
由式(11)可以得到
(13)
定义vec(·)为矩阵按列拉直运算,即vec(R)为M2×1的列向量.则式(12)可写为
γ=FP+ε.
(14)
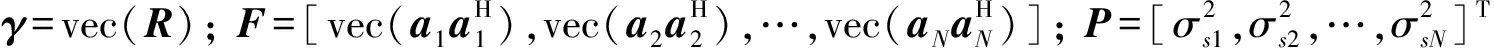
根据式(9)可得
(15)
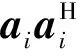
方程(14)为不相容方程组,采用标准的最小二乘法来估计功率矢量P,定义目标函数
J=(γ-FP)H(γ-FP),
(16)
令∂J/∂P=0得到
FHFP=FHγ.
(17)
方程(17)即方程(14)的最小二乘解满足的代数方程,它是一个相容方程组[11].如果F列满秩,即FHF满秩,则方程(17)有唯一解
P=(FHF)-1FHγ.
(18)
也即方程(14)的最小二乘解.
P=(FHF)+FHγ.
(19)
为了提高目标亮温分布的空间分辨率,要求空间区域划分较细,即信源数目N较大.因此为了准确求解功率分布,则要求2LM+1越大越好.LM实际上为阵列的孔径大小,因此为提高空间分辨率需要大口径阵列.由于均匀阵列的F矩阵中有大量的重复项,可以采用稀疏阵列,这一方面增大阵列孔径,另一方面可以减少阵元数,简化系统结构.
从上面分析可以看出,采用阵列信号处理算法反演辐射目标亮温,与综合孔径中的BG算法类似,F矩阵对应于综合孔径中的G矩阵.而2LM+1实际上为空间频率采样数[12].在综合孔径中,阵列孔径增大,对应于空间采样频率的增大.两者也有较大区别,主要在如下几个方面:1)综合孔径算法通过两基线接收数据的相关运算来提取功率信息,由于辐射信号是不相关的,因此需要相干本振源来提供相关性.而阵列信号处理算法正是利用辐射信号以及噪声的不相干特性,利用协方差矩阵来提取目标亮温分布特性,接收结构更加简单.2)阵列处理算法属于参量算法,由式(14)可以看出,只要采用优化算法、降低噪声等措施,可以进一步提高反演准确性.而综合孔径算法属于空域傅里叶变换,受限于阵列空间频率采样的限制,反演精度难以进一步提高.3)采用阵列信号处理算法来处理阵列误差时,只要在阵列导向矢量矩阵A中考虑通道增益的不一致性就可以简单直接地进行描述,并利用优化算法进行校正.而采用综合孔径算法由于对接收数据进行两两基线相关运算,使得其G矩阵误差校正非常麻烦.4)由方程(14)可以看出,阵列信号处理中背景噪声分量由ε=vec(σ2I)描述.因此只要有噪声分布特性,平均功率等先验信息,就可以从信号协方差向量γ中去除噪声影响,从而提高反演精度[10].而综合孔径算法中,辐射信号和噪声不可区分,造成反演误差难以去除.
2 计算结果分析
为验证上面提出的辐射目标阵列处理算法进行计算验证,采用一维16单元最小冗余阵列,单位间距u=d/λ=0.5,阵元相对位置为:[0,1,2,8,14,20,31,42,53,64,75,80,85,88,89,90].阵列最大基线长度为91u.显然,这里不是等距均匀线阵,利用虚拟阵列变换法,该16单元最小冗余阵列可以等效变换为91单元的均匀等距线阵(ULA).按该阵列分布,综合孔径算法的空间分辨率(3 dB波束宽度)为0.56°[2].
设两空间目标的入射角度分别为-0.75°,0.75°,间隔1.5°.图2给出利用阵列信号处理的MUSIC反演的目标的空间谱曲线,图3给出了利用综合孔径傅里叶反演算法得到的归一化亮温曲线.空间谱估计的两信号角度分别为-0.747°,0.747°,平均偏差为0.004 2°,相对误差0.5%.综合孔径计算得到的角度分别为-0.762°,0.762°,偏差为0.017°,相对误差为2.3%.可以看出在一个分辨单元之外,空间谱算法和综合孔径算法都能良好地分辨,但空间谱算法得到的结果更加准确,精度比傅里叶反演算法要高4倍.
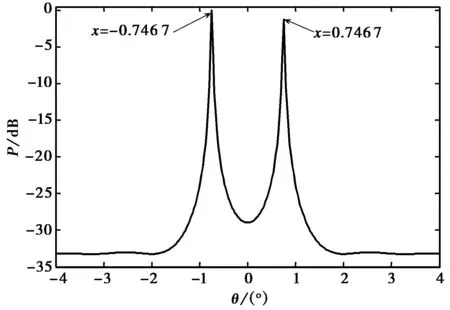
图2 目标间隔1.5°时空间谱曲线

图3 目标间隔1.5°时傅里叶反演亮温
当两空间目标的入射角度分别为-0.2°,0.2°,间隔0.4°时,已经低于综合孔径的分辨极限.从图4可以看出,空间谱算法仍能良好地分辨两信号,估计得到的角度分别为-0.21°,0.21°,偏差为0.014 1°,相对误差为5%.如图5所示,综合孔径算法已经不能分辨两个目标.因此,空间谱算法可以突破阵列的波束限制,实现阵列波束内空间目标的超分辨估计.
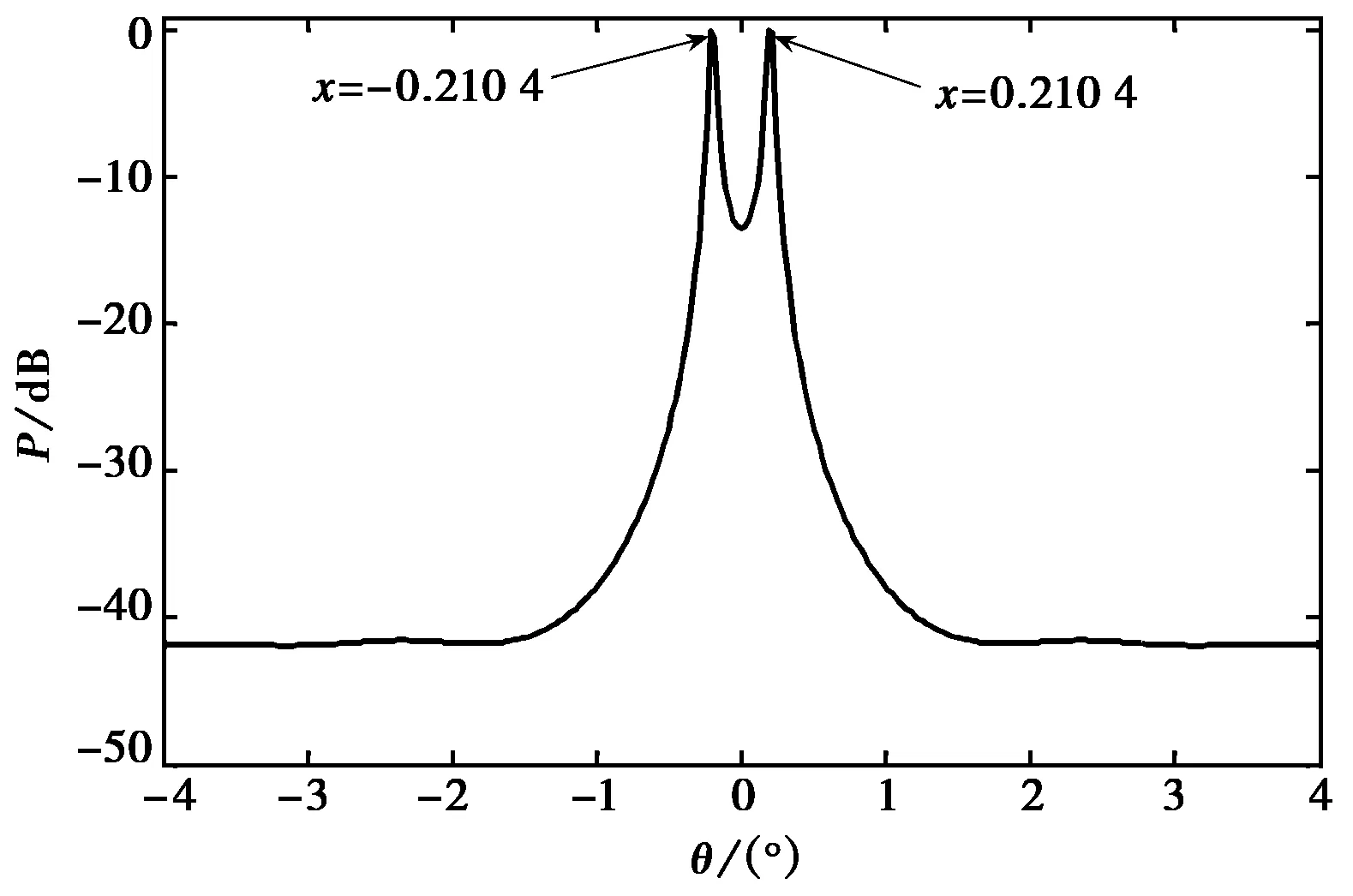
图4 目标间隔0.4°时空间谱曲线
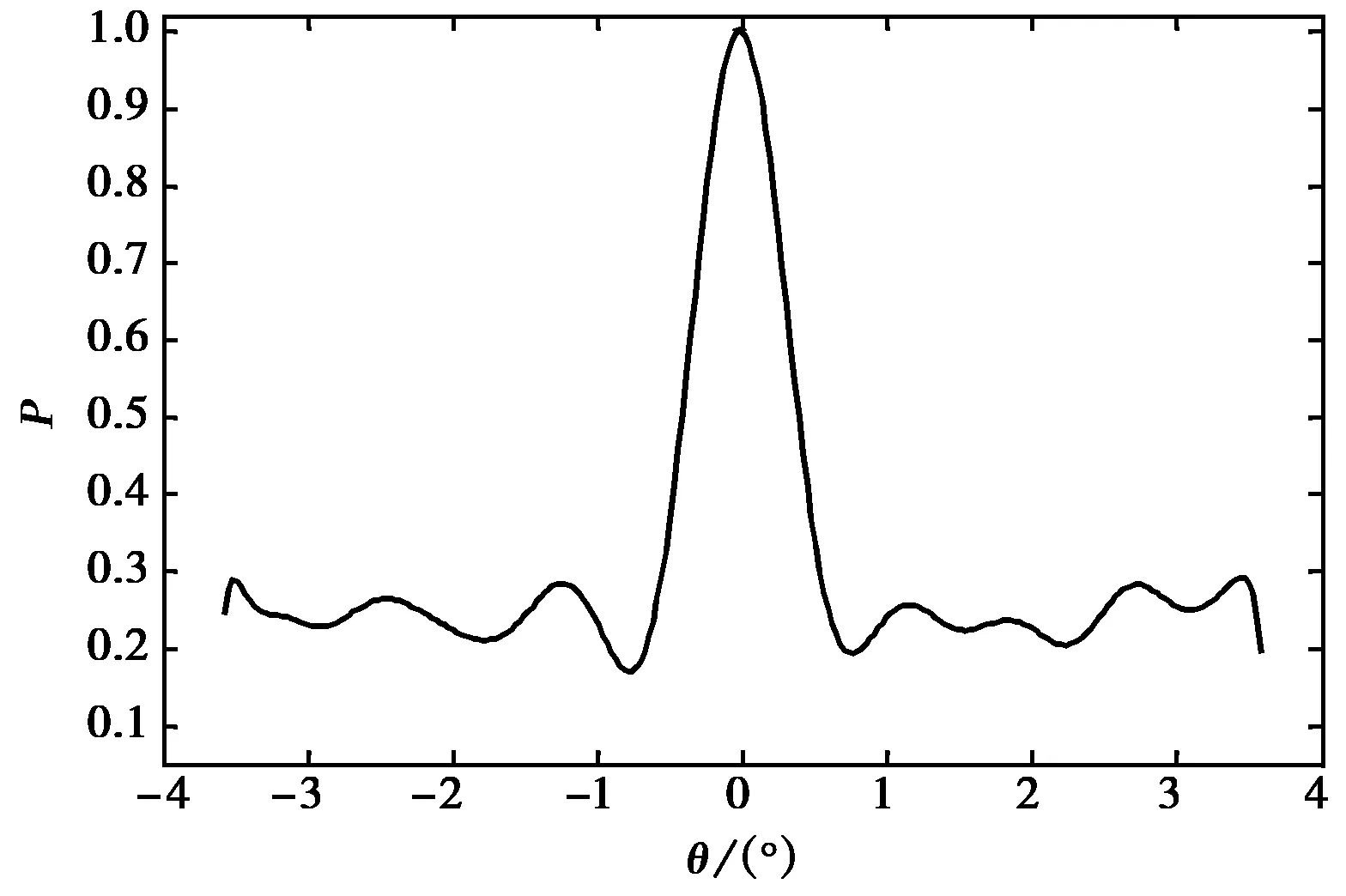
图5 目标间隔0.4°时傅里叶反演亮温
图2以及图4的空间谱曲线谱峰的横坐标对于信号的入射角度,但纵坐标并不代表信号的功率,并没有物理意义,这一点由前面理论分析已经给出.图6给出了利用阵列信号反演算法计算的目标亮温结果.而图7为综合孔径的傅里叶反演算法得到的归一化亮温分布.从两图比较看出,本文的阵列信号处理模型算法反演的亮温分布与真实目标的亮温分布更加接近,偏差更小.通过计算得到,模型算法的偏差(均方值)为0.032 3,而傅里叶反演算法的偏差(均方值)为0.170 4,可见本文模型算法精度更高.另外从图6还可以看出,模型算法反演的亮温与目标的真实亮温分布的误差体现为随机分布,原因如上分析,本文的阵列信号处理算法属于参数优化算法,只要提高信噪比或者增大数据快拍数,利用优化算法,便可以提高精度,减小误差.而傅里叶反演算法的误差分布体现为正弦振荡的性质,这是因为综合孔径阵列的最大基线长度有限,进行空间频率采样时的高频截断导致的吉布斯振荡效应.该误差不能消除,只能加大阵列孔径,增大空间采样频率以减少误差,但这样会增加硬件系统的复杂性.

图6 阵列处理算法反演亮温曲线
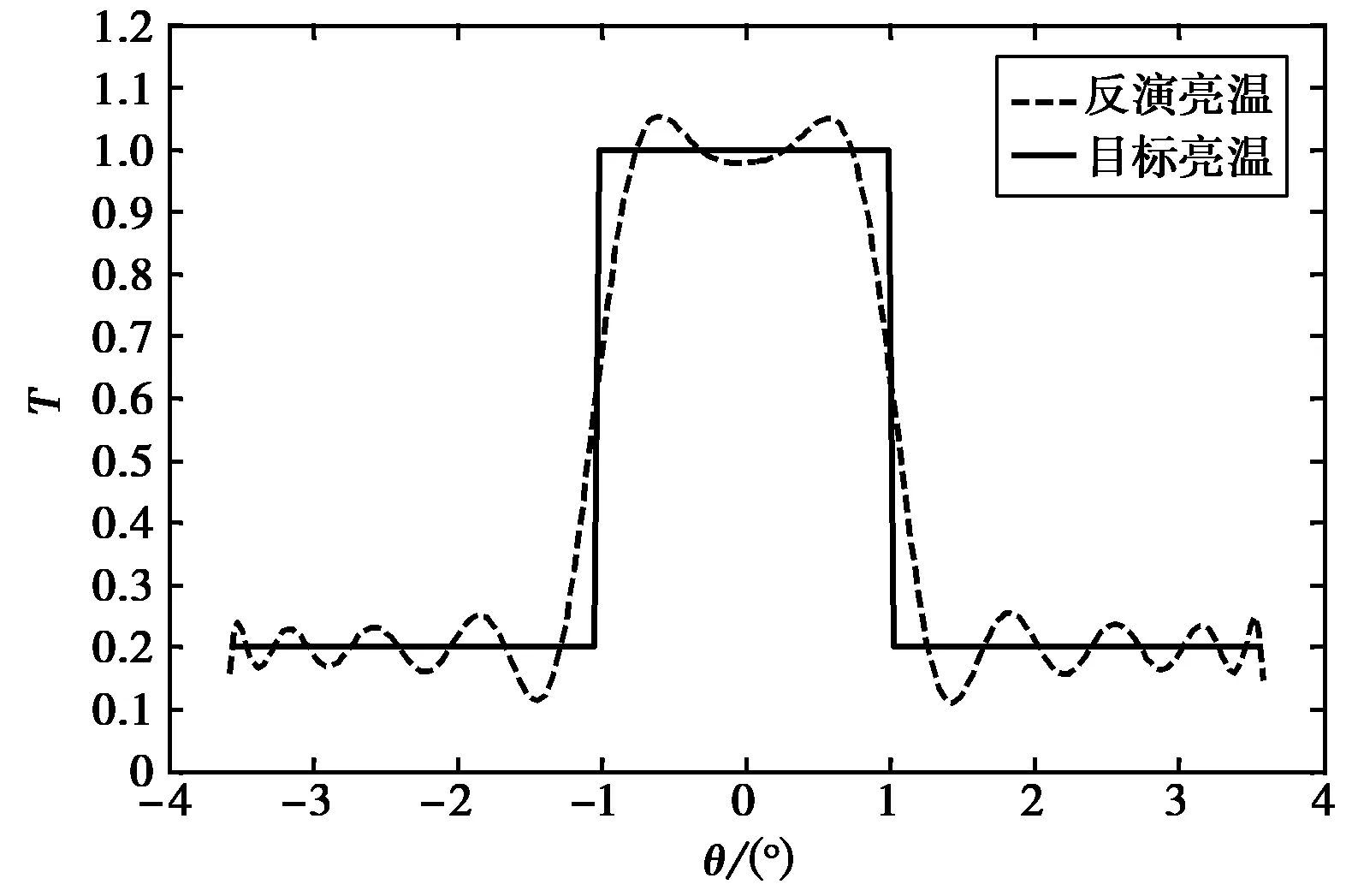
图7 综合孔径算法反演亮温曲线
图8为阵列处理和综合孔径两种算法反演的亮温相对误差随信号相关度变化趋势.两信号的相关度定义为其导向矢量的相关性[6]
(20)
式(20)的相关性实际上由两信号方向的角度差决定.当两信号角度差越大时,其相关性越小.反之,当两信号越靠近时,相关性越大.从图8可以看出,随着两信号的相关性增大,两种算法的误差都变大.在相关度较小时,算法反演误差也很小.从图中还可以看出,阵列信号处理算法相比综合孔径算法,对相关度敏感性更大,随着相关度增大,其误差迅速增高.这是由于阵列信号处理算法依赖于空间信号和噪声的不相关性,信号相关度越小,算法性能越好.在相关度变大时,算法性能降低,需要采用一些去相关的措施来校正算法.
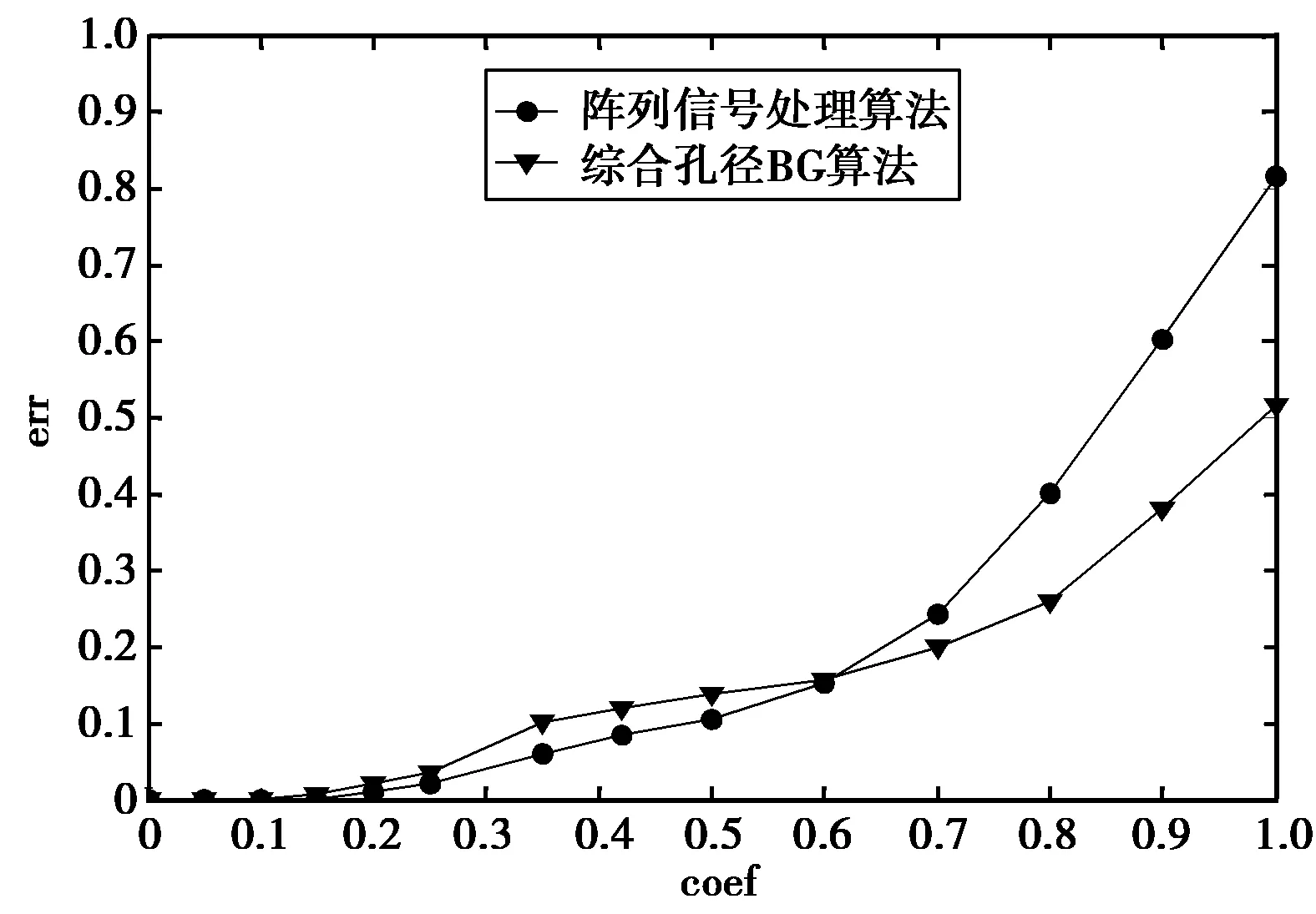
图8 亮温反演误差随信号相关度变化
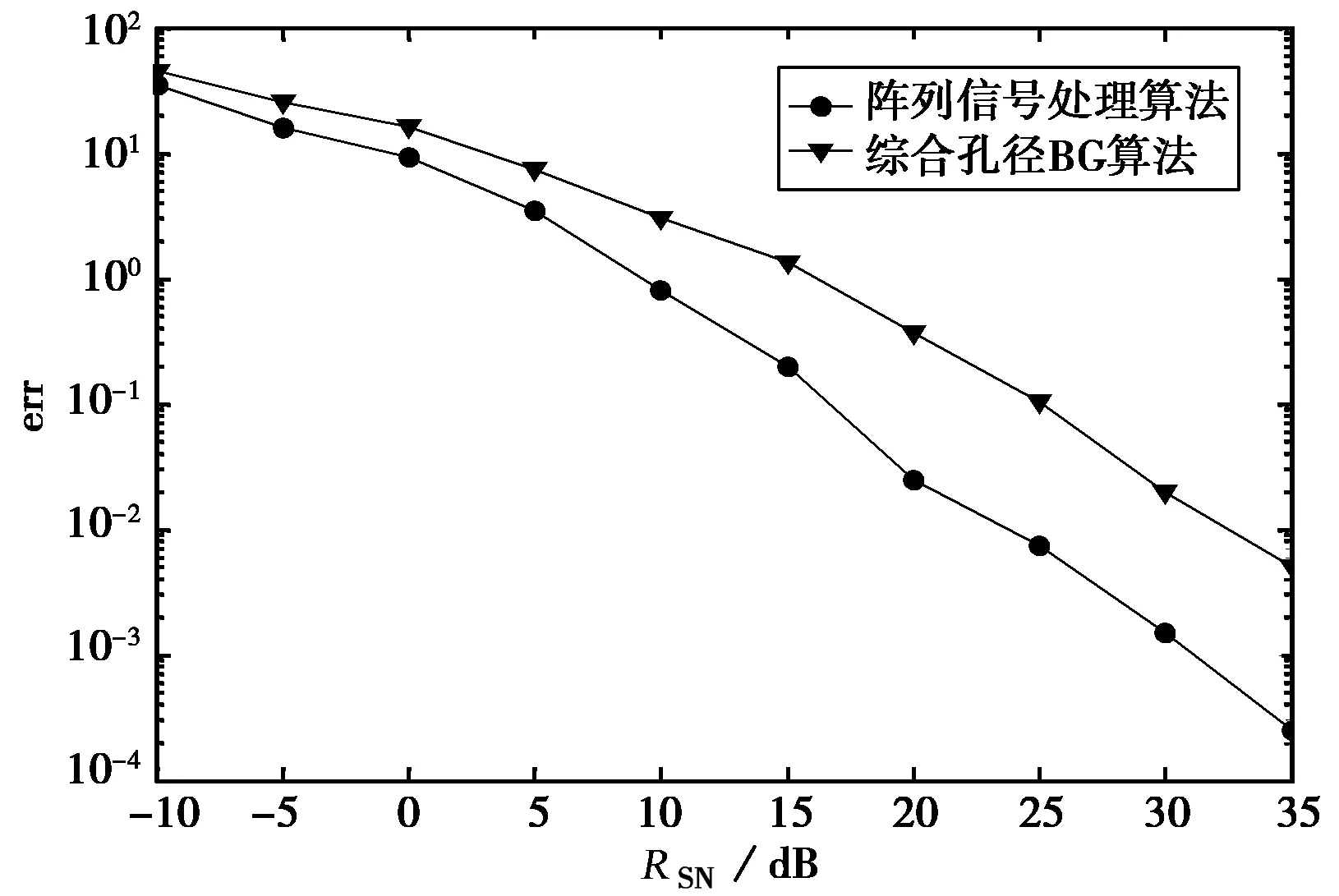
图9 亮温反演误差随信噪比变化
图9为亮温反演误差随信噪比变化趋势.如图9所示,随信噪比增大,两种算法的误差随之降低.图中还可以得出,在相同的信噪比下,阵列信号算法相比综合孔径算法,误差更低.这是由于阵列算法采用快拍数据平均的方法,根据噪声的不相关性,降低了噪声的影响,如式(11)所示,这相当于滤波的作用,提高了反演精度.由式(11)也可以看出,增加快拍数,可以进一步提高反演精度.而综合孔径算法,对通道噪声的处理能力较弱.在图中看出,当信噪比大于20 dB时,阵列处理算法反演误差已经降至10%以下,反演比较准确.而信噪比低于10 dB时,反演误差急剧增大,两种算法性能下降甚至失效.
图10为采用阵列反演算法仿真得到的目标亮温分布.仿真中以一幅位图来代表目标,位图的灰度值代表目标的亮温分布,颜色越深,代表亮温越高.图10(a)是原始位图(目标)分布,图10(b)、(c)是反演得到的亮温分布.可以看出,图10(a)和图10(b)、10(c)非常吻合,尤其在在关键点处,即图10(b)中深色区域,可以代表为被动探测中要观察的强辐射目标.经过计算其归一化偏差只有0.03 K,即3%的相对误差,反演非常准确.
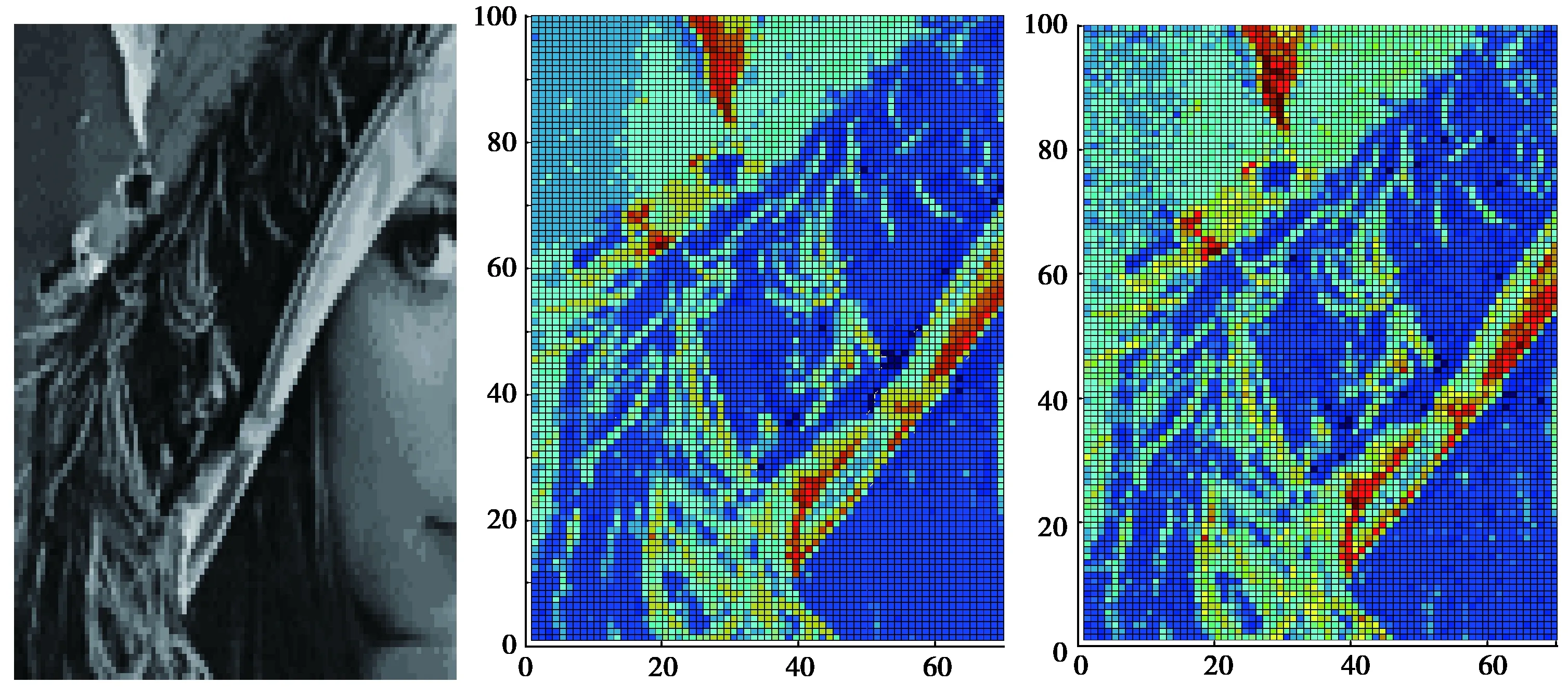
(a) 目标位图 (b) 目标亮温分布 (c) 亮温反演结果图10 阵列信号算法亮温反演
由上面分析可以看出,阵列信号处理算法可以应用于辐射目标被动探测中,因具有超越综合孔径瑞利限的空间分辨率,使得其具有对目标进行超分辨探测的能力.利用阵列信号处理算法还可以对目标分布的亮温进行反演,其反演结果相比傅里叶算法更加准确.因此,本文提出的阵列信号处理算法在辐射目标被动探测中具有应用价值.但以上仿真计算仅限于理想情况,尚有许多情况并没有考虑,例如综合孔径的稀疏阵列向阵列处理算法的均匀阵列的变换,阵列处理算法中误差的校正,辐射亮温的定标等.另外本文提出的阵列处理算法中,需要对接收数据协方差矩阵方程组进行最小二乘法求解,涉及矩阵求逆运算,计算量较大,这些问题都需要进一步研究.
3 结 论
本文基于阵列信号处理算法,建立了辐射目标被动探测亮温反演的计算模型.利用接收数据的协方差矩阵,反演得到辐射目标的信号功率.经过计算仿真验证,阵列信号处理算法相比综合孔径算法能有效突破阵列孔径限制,实现波束内目标的超分辨估计.计算发现,阵列信号处理算法性能依赖于信号相关度和信噪比,性能随相关度降低和信噪比增大而增加.本文的模型有助于进一步加深辐射目标探测技术的研究.但阵列算法复杂度大,计算时间长.在下一步的研究中,需要对算法进一步优化,并考虑阵列误差的校正,以提高实用性.
[1] 孙逢林,张升伟. 基于综合孔径辐射计稀疏阵列非均匀采样图像的快速重建[J].电子与信息学报, 2013, 35(4): 927-932.
SUN Fenglin, ZHANG Shengwei. Fast image reconstruction for non-uniform sampling of thinned array of synthesis aperture radiometer [J]. Journal of Electronics & Information Technology, 2013, 35(4): 927-932.(in Chinese)
[2] STAVROPOULOS K, MANIKAS A. Array calibration in the presence of unknown sensor characteristics and mutual coupling[C]∥ Proceedings of the European Signal Processing Conference, 2000,3: 1417-1420.
[3] SWIFT A T, D M LEVINE,RUF C S. Aperture synthesis concepts in microwave remote sensing of the earth [J]. IEEE Transactions on Microwave Theory and Techniques, 1991, 39(12): 1931-1935.
[4] 顾建峰. 阵列信号处理中若干问题研究[D].成都:电子科技大学, 2008.
GU Jianfeng. Some Researches on Array Signal Processing [D]. Chendu: University of Electron Technology, 2008.(in Chinese)
[5] 王永良, 陈 辉, 彭应宁,等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.
[6] 王永良, 丁前军, 李荣峰. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009.
[7] XU X L, BUCKLEY K, BIAS M. Analysis of the MUSIC location estimator [J]. IEEE Transactions on Signal Processing, 1992, 40(10): 2559-2569.
[8] 齐子森, 郭 英,王布等. 柱面共形阵列天线盲极化波达方向估计算法[J]. 电波科学学报, 2011, 26(2): 245-252.
QI ZISEN, GUO Ying, NANG Buhong et al. Blind DOA estimation algorithm for cylindrical conformal array with respect to Polarization diversity [J]. Chinese Journal of Radio Science, 2011, 26(2): 245-252.(in Chinese)
[9] ZHOU C, HABER F, JAGGARD D L. A resolution measure for the MUSIC algorithm and its application to plane wave arrivals contaminated by coherent interference [J]. IEEE Transactions on Signal Processing, 1991, 39(2): 454-463.
[10] 屈 蓉. 用于目标辐射探测的空间谱算法及仿真研究[D].武汉:华中科技大学, 2008.
QU Rong. Research on the Target Radiation Detection by Spatial Spectrum Algorithm [D].Wuhan: Huazhong University of Science and Technology,2008. (in Chinese)
[11] KRIM H, VIBERG M. Two decades of array signal processing research [J]. IEEE Transactions on Signal Processing, 1996, 13(4): 67-94.
[12] 王 鼎, 吴 瑛. 基于旋转不变子空间均匀圆阵互耦自校正算法[J]. 电波科学学报, 2011, 26 (2): 253-261.
WANG Ding, WU Ying. Mutual coupling self-calibration algorithm for uniform circular array based on ESPRIT technique [J]. Chinese Journal of Radio Science, 2011, 26(2): 253-261. (in Chinese)

