抛物方程方法的非均匀网格技术研究
张青洪 廖 成 盛 楠 陈伶璐
(西南交通大学电磁场与微波技术研究所,四川 成都 610031)
引 言
近年来,对流层电波传播问题的研究引起了国内外学者的广泛关注,特别是大气波导对通信系统、雷达系统以及电子系统的影响已成为各国学者关注的焦点[1-5].
抛物方程(Parabolic equation,PE)方法可以同时处理复杂大气结构和不规则地形对电波传播的影响,能在相同距离点上计算不同高度的电波衰减值,因而PE既能预测点对点之间的路径传播损耗,也可以进行区域电磁特性覆盖预测,是目前计算对流层电波传播问题最为准确、有效的模型之一[6].
自20世纪40年代Leontovich和Fock[7]首次提出PE方法以来,虽然人们在不断地研究效率高、准确性好、稳定性强的PE数值解法,但都是基于均匀网格来实现的[8-9].若整个计算域皆采用一致性细网格来描述,则势必占用过多的计算资源和较长的运算时间,这对于一些侦察远距离目标的雷达系统,将很难满足其实时性的要求;若采用一致性粗网格来描述,则会给PE的计算带来较大的误差.基于此,本文研究了PE的非均匀网格技术,在保证计算精度的同时,提高其计算效率.
目前,PE的数值解法主要有分步傅里叶解法(Split-Step Fourier Transform,SSFT)和有限差分解法[10-11].在大尺度传播环境中,SSFT可方便地用于计算传播空间媒质变化、地形起伏变化及地表电磁参数变化等条件下的电波传播问题[12].另外,相对于有限差分解法,SSFT是一种采用了快速傅里叶变换(Fast Fourier Transform,FFT)技术的频域算法,在步进求解过程中,其步长几乎不受波长的限制,因此适合与非均匀网格技术相结合.本文将采用SSFT研究PE的非均匀网格技术,并利用该技术求解复杂大气结构中不规则地形上的电波传播问题以及研究非整格点上的场值求解方法,同时将计算结果与传统PE进行对比,以验证该算法的高效性.
1 抛物方程的非均匀网格技术
设电磁场时谐因子为e-iωt,在直角坐标系(x,y,z)下,假设ψ为任意场分量,且与y无关,则对于水平极化波,只有Ey为非零的电场分量,即ψ(x,z)=Ey(x,z);对于垂直极化波,只有Hy为非零的磁场分量,即ψ(x,z)=Hy(x,z).在电波传播过程中,ψ满足二维标量波动方程[13]
(1)
式中:k0为真空中的传播常数;n为媒质的折射率.定义沿x轴正向传播的波函数为
u(x,z)=e-ik0xψ(x,z),
(2)
将u(x,z)代入波动方程(1)中可得
(3)
假设在电波传播过程中折射指数n不随距离x变化,将式(3)分解化简可得前向抛物方程

(4)
式中:Q为伪微分算子,且
(5)
由于存在伪微分算子Q,在复杂的边界条件下方程无法得到解析解,必须对Q作近似处理,通过数值方法来求解.采用Feit-Fleck近似[14],可以得到Feit-Fleck型宽角PE方程为
ik0(n-1)u(x,z).
(6)
利用SSFT算法求解可得
(7)
SSFT是一种步进算法,因此必须先计算场的初始值才能步进求解.抛物方程初始场的求解公式为
ug(x0,z)
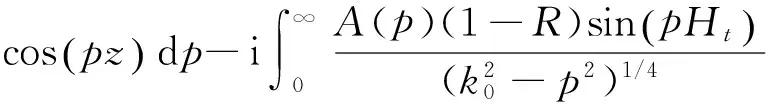
sin(pz)dp).
(8)
式中:A(p)为发射天线的方向图函数,且p=k0sinα;Ht为天线的高度;R为地面的反射系数,计算公式如式(9)
(9)

2 数值算例
2.1 水平地面电波传播特性仿真及分析
为了验证PE方法非均匀网格技术的有效性,本文先仿真了电波在水平地面上的传播特性,并将其仿真结果与采用均匀细网格及双射线法计算的结果进行对比.
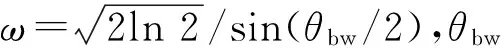
图1为电波传播至50.04 km处不同高度上的传播因子.由图1可知:PE采用非均匀网格技术计算的结果与采用均匀细网格及双射线法计算的结果吻合很好,由此验证了抛物方程非均匀网格技术的有效性.
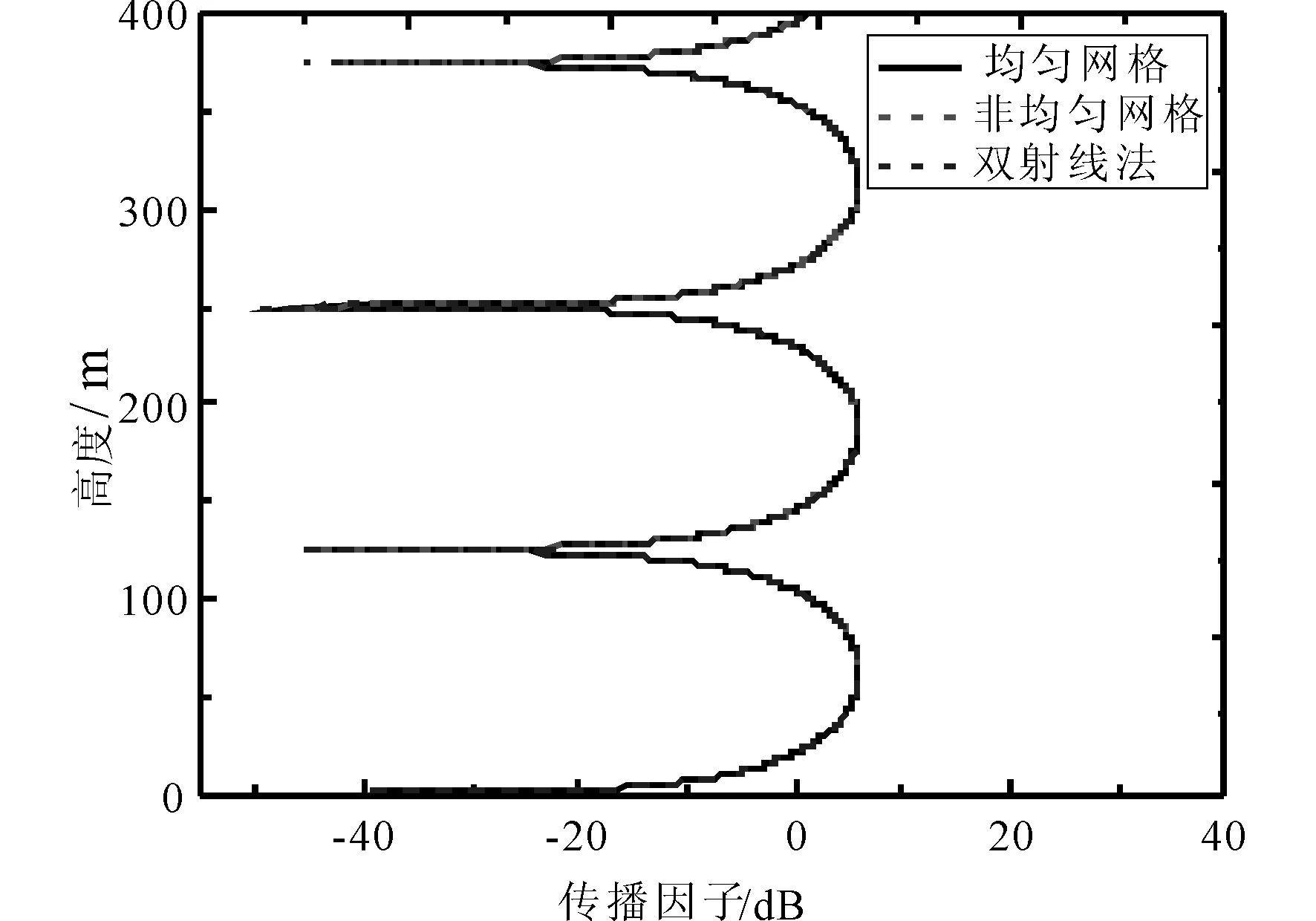
图1 电波传播50.04 km时不同高度上的传播因子
表1为分别采用均匀细网格和非均匀网格时PE计算所需要的网格空间(水平网格数×高度网格数)和计算时间对比.
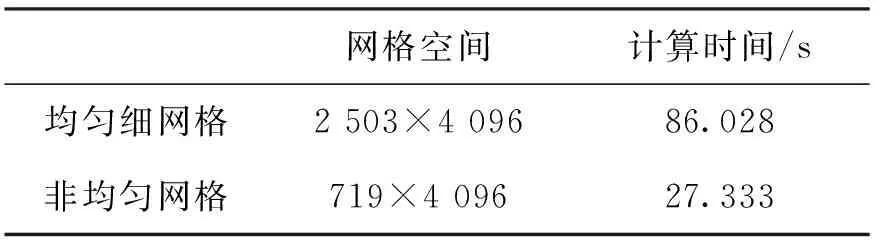
表1 网格空间和计算时间对比
从表1可以看出:采用非均匀网格技术的PE节省了计算所占用的内存空间和所需时间,提高了计算效率.
2.2 标准大气结构中不规则地形上的电磁特性模拟及分析
本算例计算了一个包含不规则地形、标准大气结构等复杂环境的电磁特性,具体的参数设置如下:
1) 发射源信息
发射天线高25 m,发射频率为1 GHz,天线水平极化,其方向图为2.1所述的高斯方向图函数,其中:θbw=3°.
2) 环境信息
假设地面上大气为标准大气.地表的相对介电常数为15,导电率为0.03 S/m,地形剖面如图2所示,其中尖峰A高度H1= 50 m,距发射站 3.04 km,尖峰B高度H2=80 m,距发射站8 km,尖峰C高度H3=80 m,距发射站10 km,正弦山峰D的地形函数为
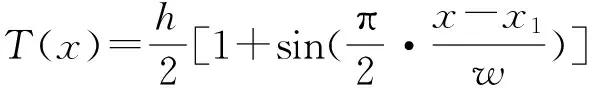
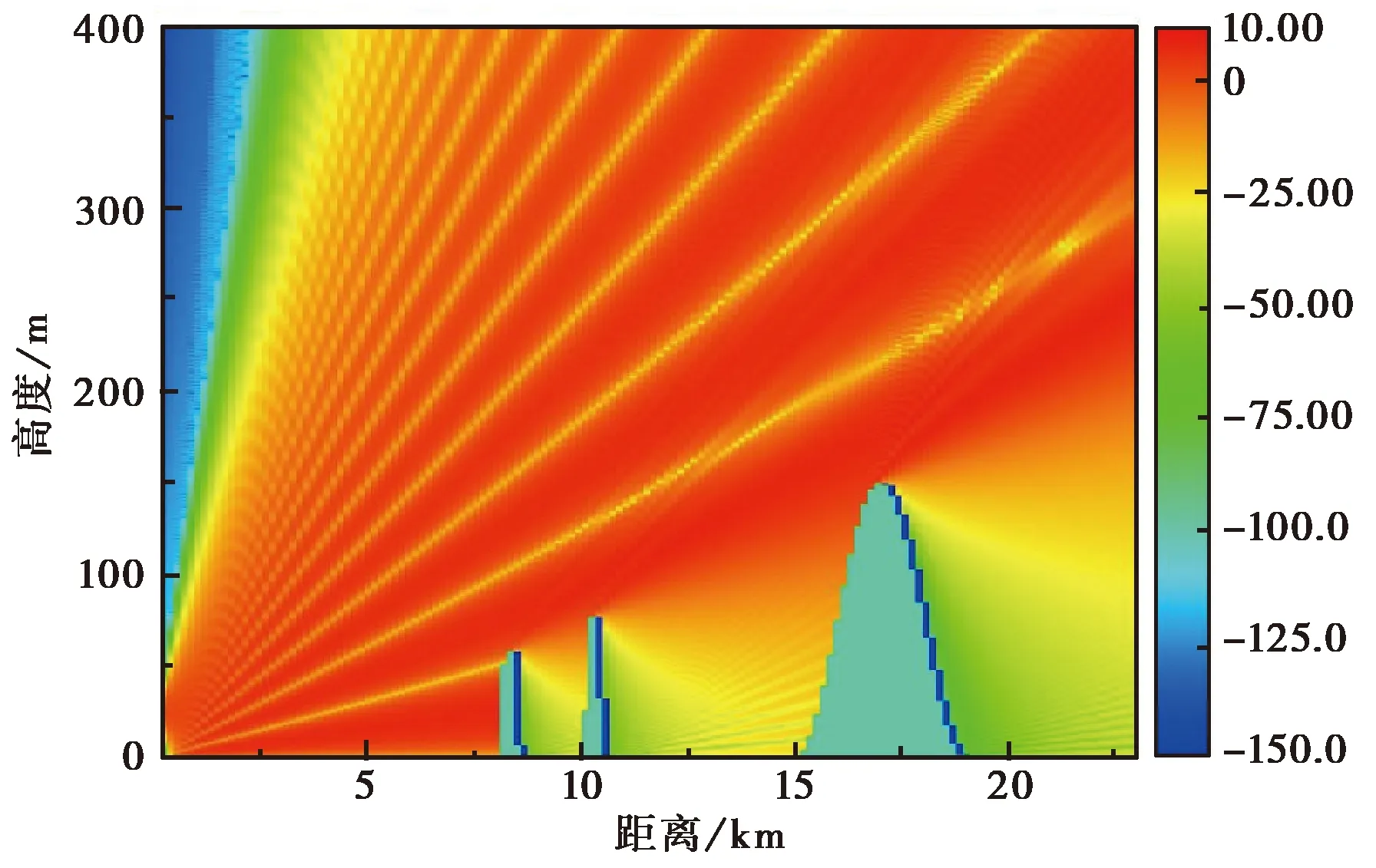
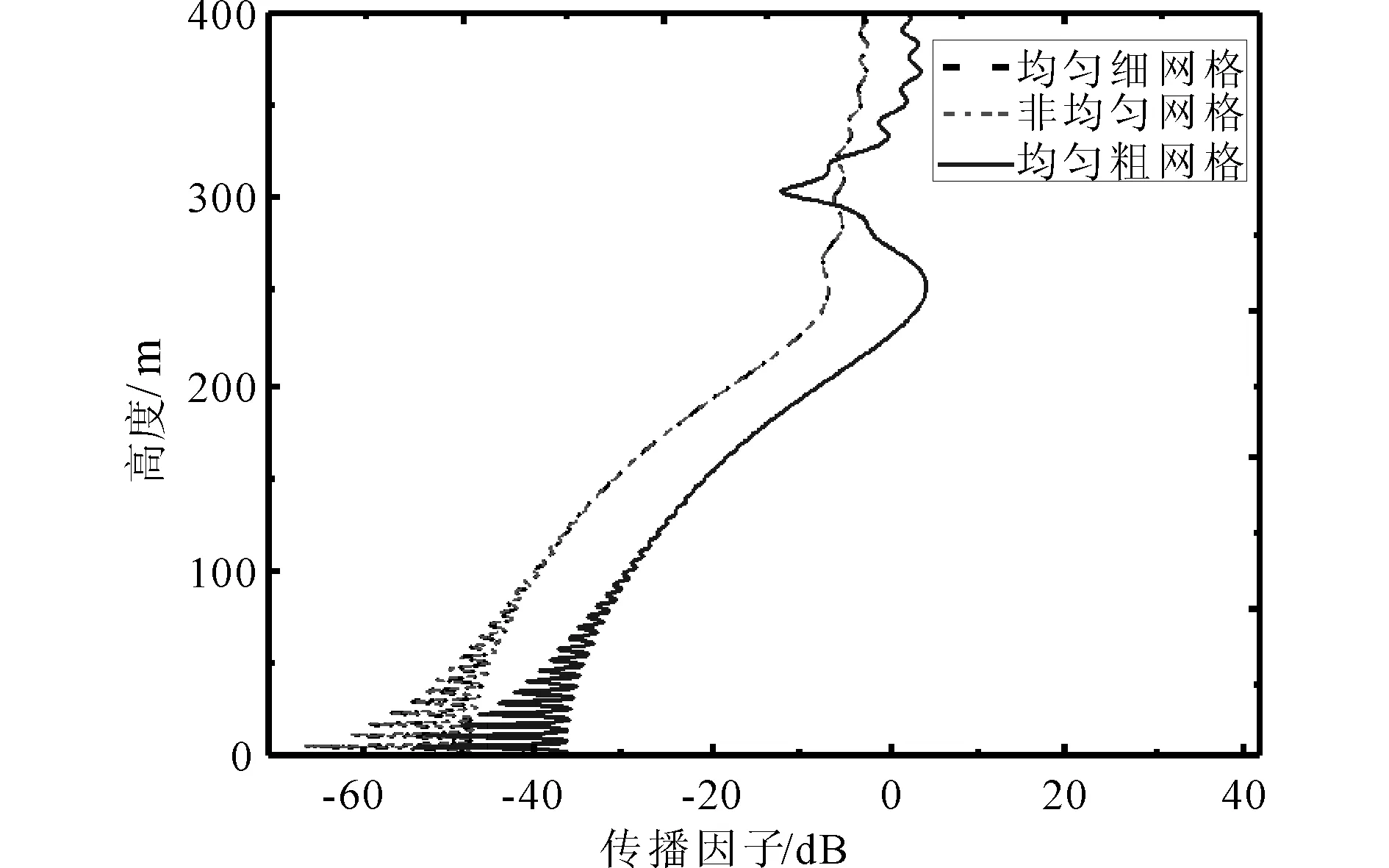
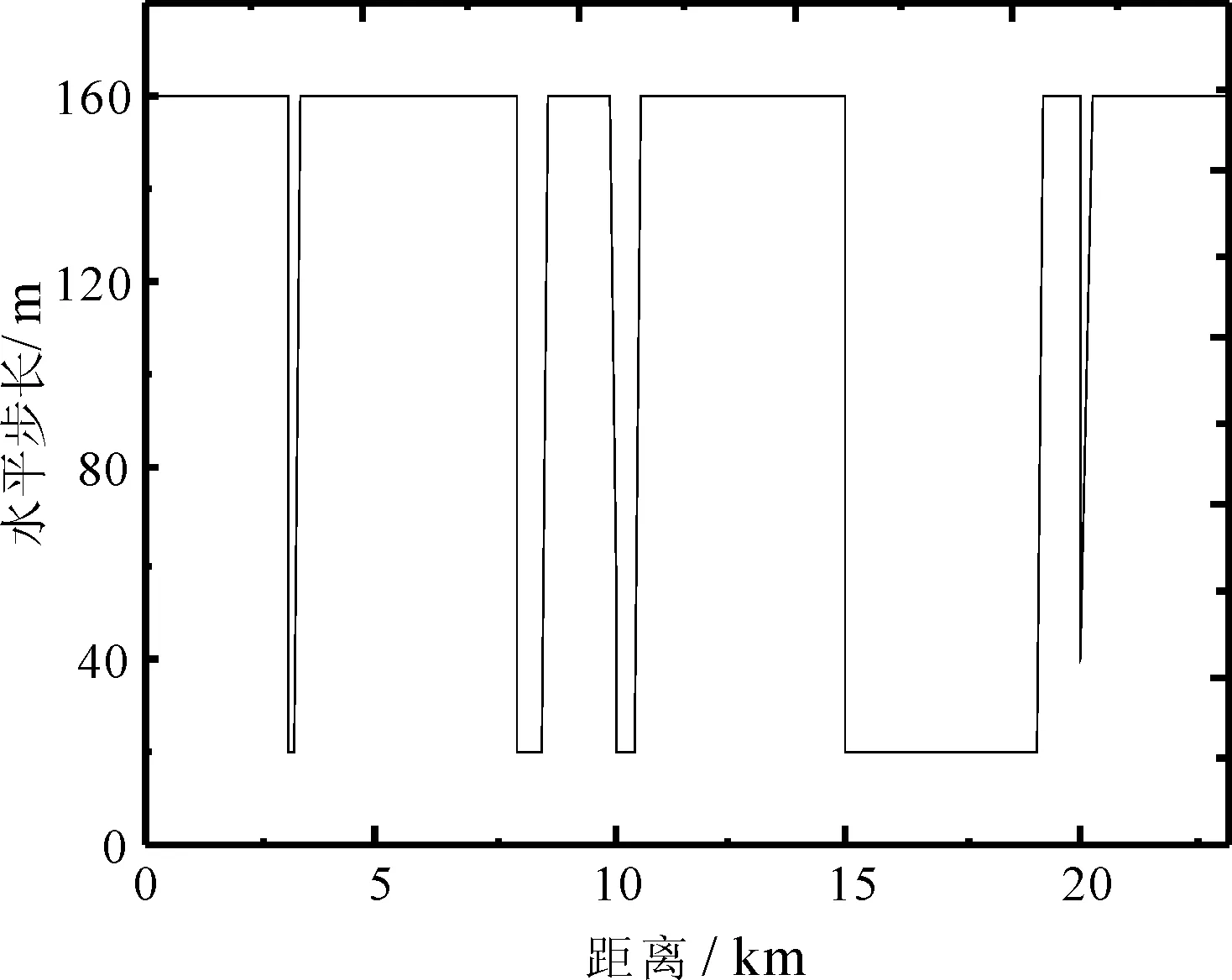
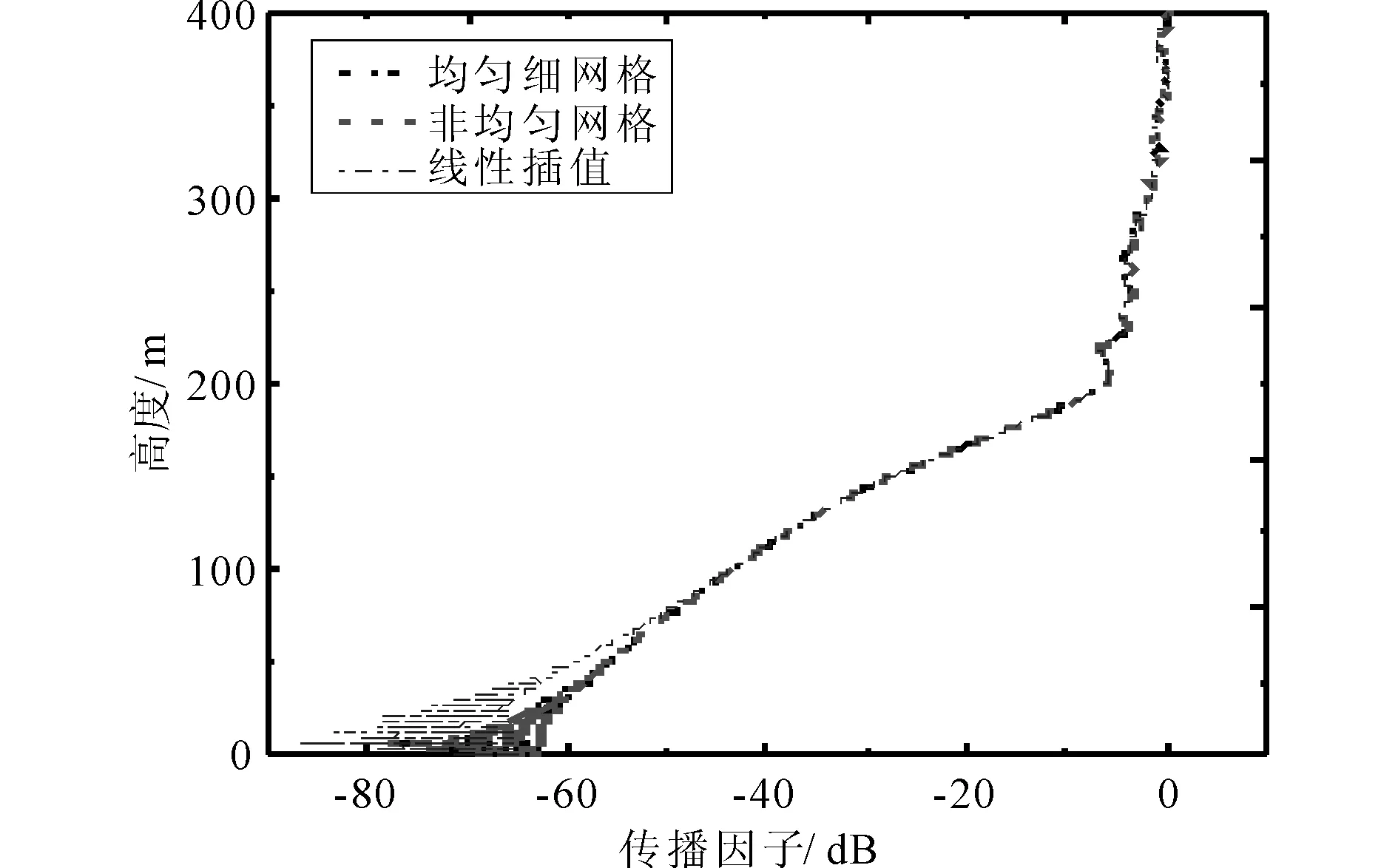
-ω (10) 式中:h=150 m;x1=16 km;w=1 km. 图2 地形剖面图 本算例中非均匀网格划分的标准为:在有不规则地形存在的区域采用细网格,而其它区域采用粗网格.图3和图4为分别采用均匀粗网格和非均匀网格计算得到的全空间电波传播因子分布伪彩图. 图3 采用均匀粗网格时空间传播因子伪彩图 图4 采用非均匀网格时空间传播因子伪彩图 由图3和图4可知:PE采用均匀粗网格计算的结果中忽略了第一个尖峰的影响,且对地形的体现也比较粗糙,而采用非均匀网格则能更好地描述地形对电波传播的影响,其计算结果更准确. 图5为电波传播至20.04 km时不同高度上的传播因子输出,并将其与PE采用均匀细网格及均匀粗网格计算的结果进行对比. 图5 电波传播至20.04 km处不同高度上的传播因子 由图5可知:PE采用均匀粗网格时计算结果产生了较大误差,而采用非均匀网格计算的结果与采用均匀细网格计算的结果吻合很好,且其计算结果更精确. 表2为分别采用均匀细网格和非均匀网格时抛物方程网格空间(水平网格数×高度网格数)及计算时间对比. 表2 网格空间和计算时间对比 由表2可知:在本算例中,相对于均匀细网格而言,采用非均匀网格技术后,PE的网格数下降达68%,计算时间减少了71%.这表明采用非均匀网格技术的PE既保证了计算精度,又极大地减少了计算所占的内存和时间,具有高效性. 图6中,r和r+Δx在整格点上,D点位于非整格点上. 图6 非整格点网格示意图 传统的PE计算过程中,非整格点处的场值一般是通过前后二格点处的场值线性插值得到,具体的插值方法为 (11) 通过采用非均匀网格技术来计算,具体就是在D处取Δx=D-r,这样就相当于把D转换到整格点上,进而求解. 采用2.2节中综合环境的算例,计算了电波传播至20 km时不同高度的衰减. 图7为不同距离处的网格步长分布图. 图7中非均匀网格采取的最小步长为20 m,最大步长为160 m,需要得到20 km处不同高度的场值.由于距离20 km不在整格点上,故它步长单独处理,此时Δx=40 m. 图8为采用非均匀网格PE计算的结果与采用线性插值及均匀细网格计算结果的对比图,算例中均匀细网格步长值为20 m,此时计算距离刚好处在整格点上. 由图8可知:PE采用非均匀网格计算的结果与采用均匀细网格计算的结果一致,比线性插值结果更准确,因此更适合于求解非整格点上的场值. 图7 非均匀网格步长分布图 图8 电波传播至20 km时不同高度传播因子对比 研究了抛物方程方法的非均匀网格技术,并结合典型对流层环境的电波传播问题对其有效性和准确性进行了验证.实例仿真了复杂大气结构中不规则地形上的电波传播特性,并将计算精度、计算时间等与均匀网格抛物方程结果进行对比.结果表明,采用非均匀网格的PE既具有良好的精度,又能减少计算内存和时间,具有综合优势,这对快速而准确地预测电磁波在复杂环境中的传播特性具有重要的意义. [1] ATKINSON B W,ZHU M.Coastal effects on radar propagation in atmospheric ducting conditions[J].Meteorological applications,2006,13(1):53-62. [2] 姚景顺,杨世兴.抛物方程模型在海上电波传播中的应用[J].电波科学学报,2009,24(3):493-497. YAO Jingshun,YANG Shixin.A terrain parabolic equation model for propagation over the ocean[J].Chinese Journal of Radio Science,2009,24(3):493-497.(in Chinese) [3] ZHAO X L,HUANG J Y,GONG S H.Modeling on multi-eigenpath channel in marine atmospheric duct[J].Radio Science,2009,44(1):1-5. [4] 康士峰,葛德彪,罗贤云,等.抛物型波方程方法研究复杂环境对雷达和通信传播的影响[J].电子学报,2000,28(6):68-71. KANG Shifeng,GE Debiao,LUO Xianyun,et al.Study on effects of the complex environment on radar and communication propagation with the method of parabolic equation[J].Chinese Journal of Electronics,2000,28(6):68-71.(in Chinese) [5] 杨 超,郭立新,李宏强,等.大气波导中电波传播特性的研究[J].西安电子科技大学学报,2009,36(6):1097-1102. YANG Chao,GUO Lixin,LI Hongqiang,et al.Study the propagation characteristic of radio wave in atmospheric duct[J].Journal of Xidian University,2009,36(6):1097-1102.(in Chinese) [6] 胡绘斌,毛钧杰,柴舜连.大气折射率剖面在宽角抛物方程中的应用[J].微波学报,2006,22(1):5-8. HU Huibin,MAO Junjie,CHAI Shunlian.Application of atmosphere refractivity profile in wide -angle parabolic equation[J].Journal of Microwaves,2006,22(1):5-8.(in Chinese) [7] LEONTOVICH M A,FOCK V A.Solution of propagation of electromagnetic waves along the earth’s surface by the method of parabolic equation[J].J Phys USSR,1946,10(1):13-23. [8] 郭建炎,王剑莹,龙云亮.森林中电波传播的抛物方程法[J].电波科学学报,2008,22(6):1042-1046. GUO Jianyan,WANG Jianying,LONG Yunliang.Parabolic equation model for wave propagation in forest environments[J].Chinese Journal of Radio Science,2008,22(6):1042-1046.(in Chinese) [9] 李广成,郭立新,吴振森,等.障碍物对蒸发波导中电波传播影响研究[J].电波科学学报,2011,26(4):621-627. LI Guangcheng,GUO Lixin,WU Zhensen,et al.Influence of obstacle towards electromagnetic wave propagation in the evaporation duct [J].Chinese Journal of Radio Science,2011,26(4):621-627.(in Chinese) [10] 胡绘斌,柴舜连,毛钧杰.宽角抛物方程在阻抗边界条件下的应用[J].电波科学学报,2005,20(4):500-504. HU Huibin,CHAI Shunlian,MAO Junjie.Application of the wide-angle parabolic equation under impedance boundary condition[J].Chinese Journal of Radio Science,2005,20(4):500-504.(in Chinese) [11] 方 剑,林为干,赵愉深.电磁波在对流层中传播的抛物化方程的有限差分解法[J].电子科学学刊,1995,17(3):315-320. FANG Jian,LIN Weigan,ZhAO Yushen.Numerical solution of the parabolic equation representing electromagnetic wave propagation in the troposphere using box method[J].Journal of Electronics,1995,17(3):315-320.(in Chinese) [12] 李德鑫,杨日杰,王元诚,等.双向DMFT算法研究不规则地形条件下的电波传播特性[J].航空学报,2011,32:1-9. LI Dexin,YANG Rijie,WANG Yuancheng,et al.Characteristics of radio wave propagation in irregular terrain environment by the twoway Improved DMFT algorithm[J].Acta Aeronautica et Astronautica Sinica,2011,32:1-9.(in Chinese) [13] LEVY M.Parabolic Equation Methods for Electromagnetic Wave Propagation[M].London:IEEE Press,2000.[14] FEIT M D,FLECK J A.Light propagation in graded -index fibers[J].Applied Optics,1978,17(24):3990-3998.


2.3 非整格点上的电场值求解
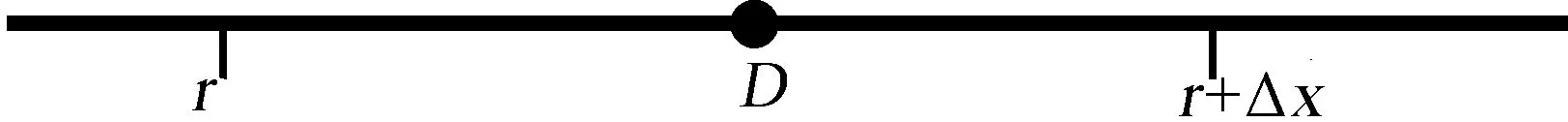
3 结 论

