基于形态学成分分析的合成孔径雷达图像去噪

王 灿 苏卫民 顾 红 邵 华

(南京理工大学电光学院，江苏 南京 210094)

引 言

合成孔径雷达(Synthetic Aperture Radar，SAR)虽然具有全天候全天时成像、高分辨和穿透性强等诸多优点，但是在SAR成像过程中，分辨单元的幅度受随机相位的影响产生类似于噪声的相干斑，相干斑严重影响了SAR图像的质量[1]，使得人们对图像目标的探测、分析和解译能力降低.所以，相干斑抑制是SAR图像处理的一个重要环节，引起了大家的广泛关注.

在过去的十几年里，很多相干斑抑制的方法被提出.传统的方法分为两类：多视处理和空域滤波处理.多视处理方法简单，但却牺牲了空间的分辨率.滤波处理方法根据像素周围局部统计特性进行自适应空域滤波，能取得比较好的相干斑抑制效果，但是处理结果严重依赖滤波器的类型、方向和大小，因此很难较好的保留纹理和边缘信息.

近几年，随着多分辨分析滤波技术的发展，基于小波变换理论的阈值去噪方法在SAR图像相干斑抑制中得到应用[2-4].这些抑制方法相对传统空域方法，能较好的实现区域平滑和纹理保留的折中，但是通用阈值去噪方法没有考虑小波系数之间的相关性，所有小波系数统一被阈值处理，有过扼杀小波系数的倾向，图像细节不能很好的保留.M.S.Crouse等人提出的基于空间域像素统计模型的去噪方法[5-8]，可以有效抑制SAR相干斑，但是对于大面积图像，基于空间域模型的去噪方法受到限制.

2005年，Donoho提出的形态学成分分析方法MCA[9]通过不同的基对图像稀疏表示可以把图像的分段光滑部分和纹理部分分离出来.MCA方法主要应用于图像修复和图像分离[10-11].在文献[9]中，MCA首次被用于相干斑抑制，但是因为它只考虑到图像的平滑部分和纹理部分，在抑制噪声的同时图像的边缘没有得到很好的保留.本文基于一个新的超完备字典利用MCA思想进行相干斑抑制.首先，把图像分为分段光滑部分，纹理部分，边缘部分；然后，根据MCA思想，用一个包含脊小波(curvelet)的超完备的字典对图像进行稀疏表示，把图像的分段光滑部分、纹理部分、边缘部分分离出来；最后利用分离出来的部分恢复图像，从而可以有效抑制噪声.同时因为图像的特征信息被稀疏表示分离出来，这种方法可以很好的保留图像的特征信息.实验结果证明了本文算法的有效性.此外，本文给出了迭代算法中迭代步长c的上界，保证了迭代算法的收敛性.

1 SAR相干斑特性分析

SAR图像相干斑被认为是一种乘积噪声,有

Y(k，l)=F(k，l)X(k，l)，

(1)

式中：Y∈RN×N表示观测图像强度；X∈RN×N表示无噪声图像强度；F∈RN×N表示相干斑噪声强度，k，l表示第k行，l列.对于L视的强度数据，F的概率密度函数服从均值为1方差为1/L的伽马分布，即

(2)

式中Γ(·)表示伽马函数.对式(1)两边进行取对数变换有

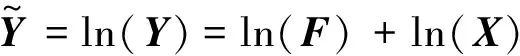
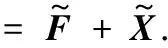
(3)

(4)

(5)

(6)

式中ψ(k，t)=(d/dt)k+1lnΓ(t)是第k阶polygamma函数.通过对数变换及式(2)～(6)可知，乘性相干斑噪声抑制问题可以转化为加性高斯噪声抑制问题.

2 基于MCA的SAR相干斑抑制

2.1 MCA

(7)

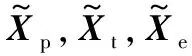
(8)

(9)

(10)

式中Φp，Φt，Φe依次记为可以稀疏表示平滑部分，纹理部分和边缘部分的基.在本文中，选择Daubechies3小波表示平滑部分的基Φp，离散余弦表示纹理部分的基Φt，curvelet小波表示边缘部分的基Φe，变换域的系数为αp，αt，αe，并且这些系数是稀疏的.所以，利用稀疏表示把图像的平滑部分，纹理部分和边缘部分分离就称为(MCA)[12]

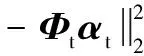
(11)

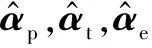
2.2 迭代收缩算法SAR相干斑抑制

式(11)的求解是一个复杂的过程，所幸近几年来，已经出现了很多算法，常用的有连续子空间最优化算法、快速迭代软阈值算法和共轭梯度法[12-13].本文使用的是快速迭代收缩算法中的可分离代理函数法[14]，这种算法是由Daubechies 2004年提出的.为了表示方便，设

Φ=[Φp，Φt，Φe]；

(12)

α=[αp，αt，αe].

(13)

暂时忽略TV项.式(11)表示为

(14)

根据Daubechies的理论，添加下面一项为

(15)

式中，参数c的选择必须保证函数dist是严格凸函数，也就是需要它的Hessian矩阵是正定的，即

cI-ΦTΦ>0，

(16)

式中，I表示单位矩阵.c必须满足条件

(17)

式中λmax(·)表示最大特征值.结合式(14)和(15)，新的目标函数表示为

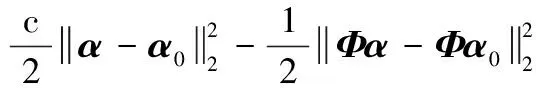
(18)

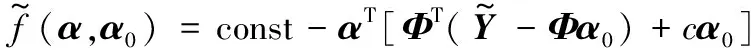
(19)

(20)

则式(19)再次简化为

(21)

至此，式(18)的最优化问题最终简化为酉形式的最优化问题[15].酉形式的最优化问题求解分为两步，首先计算

(22)

利用收缩因子限制υ0的元素数目从而获得估计值，其中收缩因子为

(23)

收缩因子把比较小的值映射到零，其他的值也向零收缩.最终得到α的最优估计值为

αopt=Sλ/c(υ0)

(24)

所以α的迭代公式为

(25)

把TV项考虑进去，分解的迭代公式如下：

(26)

式中：H是非抽样Haar小波字典;Sγ表示以γ为阈值的收缩因子.与收缩去噪算法类似，利用冗余Haar小波收缩因子估计TV修正项.

根据上述讨论，基于MCA的SAR图像相干斑抑制算法的主要处理步骤如下：

(27)

设置初始图像冗余部分为

(28)

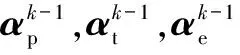
(29)

3) 更新图像冗余：

(30)

4) 转到第(2)步，直到满足收敛准则.

5) 最终输出迭代估计稀疏系数为

(31)

6) 得到去噪后的图像：

(32)

2.3 字典的选择

选择合适的字典是本算法的一个关键.字典必须能稀疏表示图像的平滑部分、纹理部分和边缘部分，它依赖于图像的特征.根据多分辨分析的思想，小波变换的过程是图像的分解过程，把图像分了低频部分和高频部分，而非零系数主要集中在图像的低频部分，也就是图像的平滑部分，所以选择Daubechies3小波变换稀疏表示图像的平滑部分.

离散余弦变换(Discrete Cosine Transform,DCT)的基是余弦函数，余弦函数有周期振荡特性，因为纹理也具有周期变化的特点，所以本文利用DCT对图像的纹理部分稀疏表示.

Donoho于1999年提出了Curvelet变换并且构造了Curvelet的紧框架，对于具有光滑奇异性曲线的目标函数，Curvelet提供了稳定的、高效的和近乎最优的表示.Curvelet变换的最大特点是各向异性，也就是Curvelet是一种具有方向性的基原子，可以对图像多尺度多方向滤波，因此具有更强的表达图像中沿边缘信息的能力，所以本文选择Curvelet稀疏表示图像的边缘部分.

2.4 参数c的边界讨论

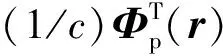
(33)

即

(34)

在迭代算法中，固定的迭代步长引起迭代精度和迭代速度之间的矛盾.针对这个矛盾，本文选择递增几何序列{ck}，它能同时提高算法性能和增加算法收敛速度.

2.5 阈值的选择

相干斑抑制过程中，阈值的选择尤为重要，它的选择直接影响到去噪效果.如果阈值太小，阈值处理后的小波系数中包含过多的噪声分量；如果阈值太大，将会丢失信号的一部分信息.针对这个矛盾，本文首先给出一个大的初始值λ/c，然后在每次迭代时逐次减少λ/c，直到减少到最小值，即

(35)

(a) 原始图像 (b) Lee滤波后的图像 (c) 小波阈值滤波

(d) 基于MCA平滑+纹理部分 (e) 本文方法 图1 真实SAR图像的滤波效果比较

3 原始数据的相干斑抑制实验

在本节，为了验证本文提出相干斑抑制算法的有效性，我们对实测机载条带SAR图像进行处理.实验数据采用的是机载雷达X波段SAR成像的图像数据，图像是单视，大小为1 024×1 024像素，图像的分辨率为1 m×1 m，图像区域包括草地、农田、公路.分别利用Lee滤波，小波阈值去噪和基于MCA平滑加纹理算法和本文算法对SAR图像进行去噪处理.其中Lee滤波算法中用到的邻域窗口大小为5×5像素，小波域阈值去噪的阈值选择为局部适应阈值.

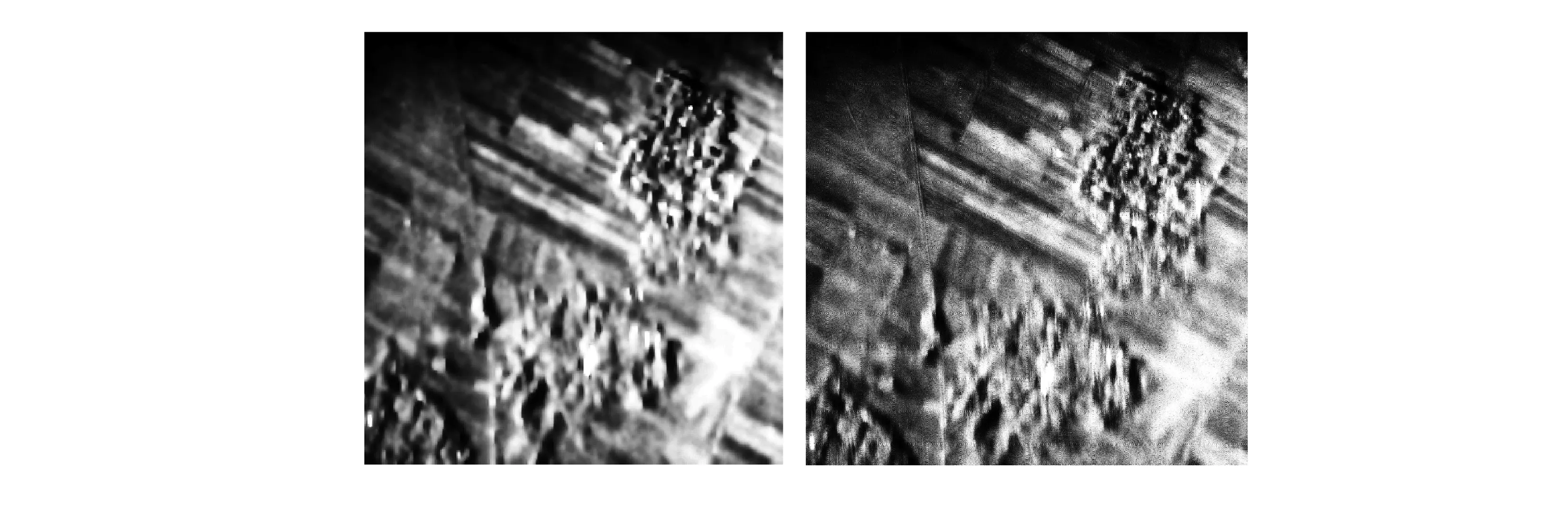
图1是SAR图像经过几种去噪算法后的效果图.图1(a)是原始SAR图像，图1(b)～(f)分别给出Lee、小波域软阈值法、MCA方法小波加DCT和本文算法滤波后的图像.可以看出Lee滤波器对噪声起到一定的抑制作用，但是带来图像的分辨率降低.小波域软阈值滤波效果好于Lee，但因为小波域软阈值法对纹理、边缘像素与噪声像素统一处理，所以不可避免地破坏了一些纹理和边缘结构.文献[7]中的方法较小波域软阈值法保留了图像的纹理信息，但是部分边缘信息丢失.本文方法利用curvelet小波稀疏表示SAR图像的边缘部分，提高了图像变换域的稀疏度，因此不仅起到了相干斑抑制的作用，而且很好的保留了图像中的纹理、边缘等有用信息.如图1方框中的局部放大图图2所示，因为原始SAR图像中相干斑的存在，图2(a)中微弱的周期信号不容易观测到，利用已有算法对SAR图像相干斑抑制后的图像如图2(b)～(d)所示，因为图像的细节丢失，周期信号也丢失，而经过本文算法处理过的SAR图像在抑制相干斑的同时，保留了图像的细节信息，微弱的周期信号也可以清楚的观测到，如图2(e)所示.

(a) 原始图像 (b) Lee滤波后的图像 (c) 小波阈值滤波

(d) 基于MCA平滑+纹理部分 (e) 本文方法 图2 真实SAR图像的滤波效果的放大图

表1列出通过不同算法滤波后图像的等效视数和比值图像的均值，由表1可知，本文方法在等效视数上是最高的，说明本文方法能有效地抑制同质区域的相干斑，并且由于我们使用超完备字典对SAR图像的有用信息进行了稀疏表示，所以在图像保持程度上也是最好的.

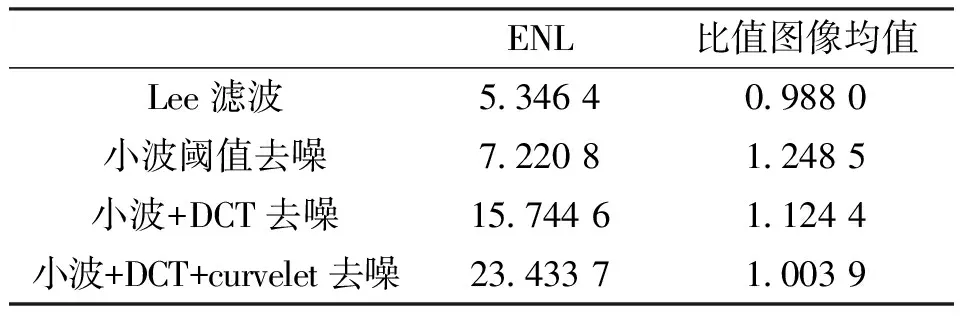
表1 不同算法的等效视数和比值图像均值

4 结 论

利用curvelet能够对图像边缘信息稀疏表示的特点，本文提出了一种基于形态学成分分析的SAR图像相干斑抑制方法.该方法根据形态学成分分析把图像分成平滑部分、纹理部分和边缘部分，然后利用一个超完备字典中的不同基，通过迭代算法对图像的平滑部分、纹理部分和边缘部分分别进行稀疏表示，从而保留了图像的有用信息，抑制了相干斑.实验证明：与小波域等SAR图像相干斑抑制方法比较，本文提出的算法在抑制相干斑的同时，提高了图像边缘等细节特征的保持能力，是一种稳定，有效的处理方法.另外，本文还给出了迭代算法步长的上界，保证了算法的收敛性.

[1] GOODMAN J W.Some fundamental properties of speckle[J].JOSA.1976，66(11):1145-1150．

[2] 陈 曦，张 红，王 超.基于AOS非线性扩散的SAR图像去噪研究[J].电波科学学报.2004，19(004):405-408．

CHEN Xi，ZHANG Hong，WANG Chao.A study of SAR images denoising based on AOS nonlinear diffusion[J].Chinese Journal of Radio Science，2004，19(004):405-408.(in Chinese)

[3] GAGNON L，JOUAN A.Speckle filtering of SAR images:A comparative study between complex-wavelet based and standard filters[C]∥Processing of The International Society for Optical Engineering. San Diego，1997．

[4] DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory，1995，41(3):613-627．

[5] VEGA M，MATEOS J，MOLINA R，et al.Bayesian TV denoising of SAR images[C]∥IEEE International Conference on Image Processing. Brussels，2011：165-168．

[6] PARRILLI S，PODERICO M，ANGELINO C V，et al.A Nonlocal SAR Image Denoising Algorithm Based on LLMMSE Wavelet Shrinkage[J].IEEE Transactions on Geoscience and Remote Sensing，2012，50(2):606-616．

[7] 吴 艳，王 霞，廖桂生.基于小波域隐马尔可夫混合模型的 SAR 图像降斑算法[J].电波科学学报.2007，22(2):244-250．

WU Yan，WANG Xia，LIAO Guisheng.SAR images despeckling based on wavelet and hidden Markov mixture model[J].Chinese Journal of Radio Science，2007，22(2):244-250.(in Chinese)

[8] CROUSE M S，NOWAK R D，BARANIUK R G.Wavelet-based statistical signal processing using hidden Markov models[J].IEEE Transactions on Signal Processing，1998，46(4):886-902．

[9] ELAD M，STARCK J L，QUERRE P，et al.Simultaneous cartoon and texture image inpainting using morphological component analysis(MCA)[J].Applied and Computational Harmonic Analysis，2005，19(3):340-358．

[10] BOBIN J，STARCK J L，FADILI J M，et al.Morphological component analysis:An adaptive thresholding strategy[J].IEEE Transactions on Image Processing，2007，16(11):2675-2681．

[11] STARCK J L，ELAD M，DONOHO D L.Image decomposition via the combination of sparse representations and a variational approach[J].IEEE Transactions on Image Processing，2005，14(10):1570-1582．

[12] BECK A，TEBOULLE M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences.2009，2(1):183-202．

[13] PATEL V M，EASLEY G R，CHELLAPPA R.Component-based restoration of speckled images[C]∥ IEEE International Conference on Image Processing.Brussels，2011：2797-2800．

[14] DAUBECHIES I，DEFRISE M，DE MOL C.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].Communications on pure and applied mathematics，2004，57(11):1413-1457．

[15] ZIBULEVSKY M，ELAD M.L1-L2 optimization in signal and image processing[J].IEEE Signal Processing Magazine，2010，27(3):76-88．

[16] 徐 丰，金亚秋.多方位高分辨率SAR的三维目标自动重建(二)多方位重建[J].电波科学学报，2008,23(1):23-33．

XU Feng，JIN Yaqiu.Automatic reconstruction of 3D objects from multi-aspect part Ⅱ:Multi-aspect reconstruction[J].Chinese Journal of Radio Science.2008,23(1):23-33.