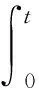一种带有自权重的积分波动率的非参估计*
李翠霞,郭二林,包美娟
(兰州大学数学与统计学院, 甘肃 兰州 730000)
波动率也称为易变性,是对金融市场风险程度的估计。从统计角度看,它是以复利计的标的资产投资回报率的标准差。从经济意义上解释,产生波动率的主要原因来自以下三个方面:宏观经济因素对某个产业部门的影响,即所谓的系统风险;特定的事件对某个企业的冲击,即所谓的非系统风险;投资者心理状态或预期的变化对股票价格所产生的作用。

一般而言,金融市场中的信息是连续的影响证券市场价格的运动过程的,数据的采集频率越低,信息丢失越多;反之,采集频率越高,信息丢失则越少。因此,金融高频数据一出现,就成为了金融领域的研究热点。20世纪90年代后期以来,国际上兴起了对金融高频时间序列的研究热潮。高频时间序列研究的代表人物是Andersen和2003年诺贝尔经济学奖得主Engle的学生Bollerslev,他们对高频时间序列的波动率采用“已实现”波动率(Realized Volatility,RV)的全新概念来度量[1-5]。

dXt=btdt+σtdWt,t≥0
(1)
这里W是一个标准布朗运动,b是一个随机可适过程。以此形式代表股票的对数价格在金融工程中已经得到了广泛的认可。
在本文中我们关心的中心问题就是如何来估计
(2)
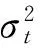
由于它在金融工程中的重要性,大量的学者已经对积分波动率的估计进行了研究[6-7],但是我们必须强调的一点是,上面提到的工作[1-7]都是基于我们这里讨论的特殊情形,即:f=1时进行的,而针对一般的函数,对的估计就显得十分重要。一方面,从数学角度上看,有了函数后,对的估计就变得非常复杂。另一方面,在实际工作中,我们往往需要的是的一个函数f(X)的积分波动率的估计,而不仅仅是的积分波动率的估计。如前面提到的股票价格的对数过程Xt可以用伊藤扩散过程来刻画,而实际中我们观察到的仅仅为St=f(Xt)=eXt。此时,积分波动率的估计就变成了I=
本文中,我们对I给出了一个新的非参数估计量n,此估计量被证明是依概率收敛到I的,同时对于此估计量,我们还得到了它的渐近正态分布。而针对该渐近正态分布,我们给出了一个学生化的表达式,从而对此估计量可以构造置信区域并做相应的假设检验。最后的模拟数据以及直方图与QQ图也说明了我们提出的估计量的收敛是一致有效的。
1 模型假定



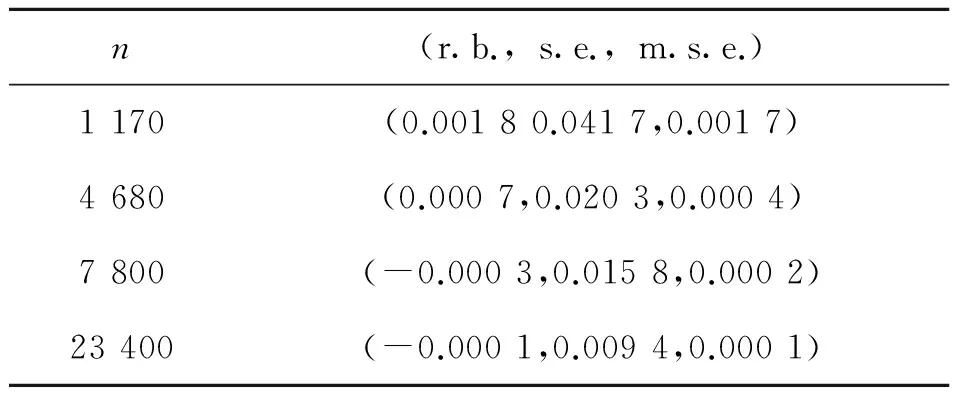
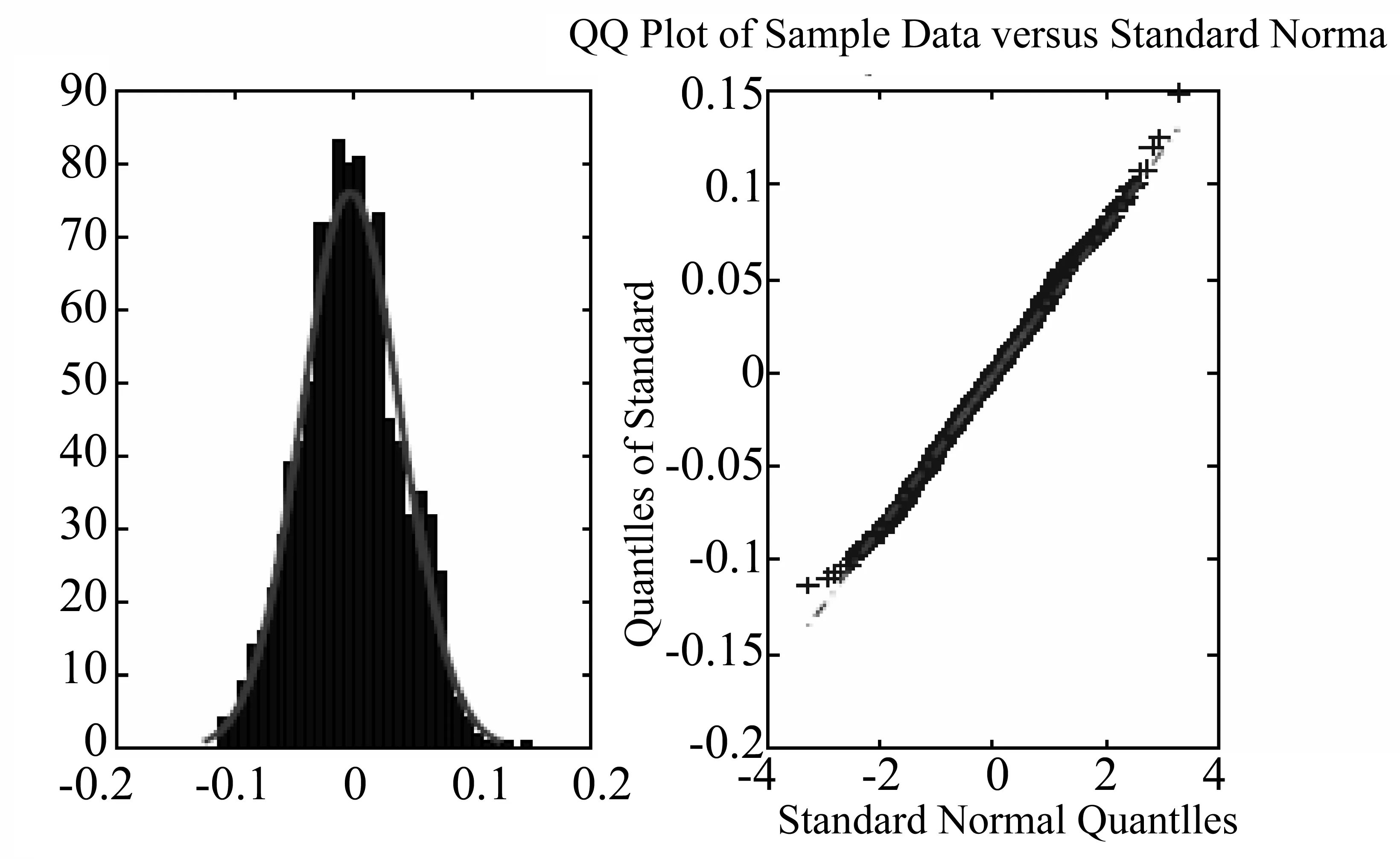
假设X的观察时刻为0=t0 假设3 假设函数f是α-李普希兹函数,即存在常数C,к> 0以及α∈ (0; 1] 使得,对任意的x,u有:|f(x)-f(u)|≤C|x-u|α(1+|x|2κ+|u|2κ)。 在本节中,我们考虑在结构(1)下对(2)中的函数进行估计。我们定义: (3) 则我们有下面的定理成立: 定理1 大数定律)在假设1-3成立的情形下,我们有下面的结论: 证明 其中由假设3,我们有: 从而,最后一个不等式成立。 现在,我们来证明中心极限定理。为此,我们先给波动过程一个结构上的假定。 假设4 假设波动函数σ={σt,t≤0}满足方程: 假设4是证明中心极限定理时所需的一个标准假设,在中心极限定理中,我们需要一个关于依分布平稳收敛的概念,现在,让我们来简单地叙述一下此概念。 ≤x,A)=P(X≤x,A) 定理2 (中心极限定理)假设1-4成立,则我们有 (4) ① 由估计量的定义,知 再由假设4及伊藤乘积公式,知,对任意的s>t, ② 在这一部分,我们来证明 由条件期望的定义以及独立增量性,我们有 (5) 利用多维伊藤乘积公式,上面的第三个等式成立。再利用的定义,我们还有 (6) 成立。 联合(5)式和(6)式,由黎曼积分,即得 (7) 由此,我们可以得到中心极限定理的一个学生化形式,利用此形式即可以找出相应的置信区间,从而对该估计量做对应的假设检验。 推论1 假定定理2成立,则有 (8) 我们按一个交易日6.5个小时计算,每20,5,3,1秒取一次数据,即分别取n=1 170,4 680,7 800,23 400时来模拟。在这里,我们把股票的对数价格取作著名的Ornstein-Uhlenbeck过程,即 这里,Wu是一个标准布朗运动。 我们重复运行1 000次,结果包含了相对偏(relative bias),标准误差(standard errors)与均方误差(mean square errors)。同时给出的一些QQ图也证明了我们提到的定理2,即中心极限定理是成立的。 从下表中,我们可以得出的结论是: 随着n的增大,相对偏(r.b.),标准误差(s.e.)与均方误差(m.s.e.)都逐渐减小,这和我们的理论结果是一致的。 表1 n取不同值时的模拟结果 Table 1 Simulation result for n 图1 n=23 400时的直方图与QQ图Fig.1 Histogram and QQ plot for n=23 400 图2 n=1 170时的直方图与QQ图Fig.2 Histogram and QQ plot for n=1 170 参考文献: [1] ANDERSEN T G, BOLLERSLEV T. Answering the skeptics: yes, standard volatility models do provide accurate forecasts [J]. International Economic Review, 1998, 39(4): 885-905. [2] ANDERSEN T G, BOLLERSLEV T, DIEBOLD F, et al. Exchange rate returns standardized by realized volatility are (nearly) Gaussian [J]. Multinational Finance Journal, 2000, 4: 159-179. [3] ANDERSEN T G, BOLLERSLEV T, DIEBOLD F, et al. The distribution of realized exchange rate volatility [J]. J Amer Stat Asso, 2001, 96, 42-55. [4] ANDERSEN T G, BOLLERSLEV T, DIEBOLD F, et al. The distribution of realized stock return volatility [J]. J Fina Econ, 2001, 61: 43-76. [5] ANDERSEN T G, BOLLERSLEV T, DIEBOLD F, et al. Modeling and forecasting realized volatility [J]. Econometrica, 2003, 71(2): 579-625. [6] A¨IT-SAHALIA Y, MYKLAND P. The effects of random and discrete sampling when estimating continuous-time diffusions [J]. Econometrica, 2003, 71: 483-549. [7] BARNDORFF-NIELSEN O, SHEPHARD N. Econometric analysis of realized volatility and its use in estimating stochastic volatility models [J]. J Royal Stat Soci B,2002,64:253-280. [8] PODOLSKIJ M, VETTER M. Estimation of volatility functionals in the simultaneous presence of microstructure noise and jumps [J]. Bernoulli, 2009, 15: 634-658.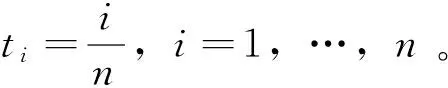
2 主要结果
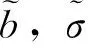



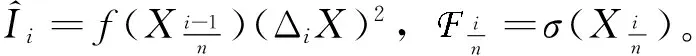

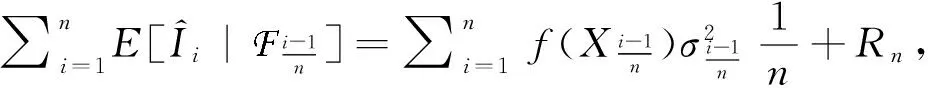
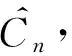

3 模拟结果