基于方位线性预测的远距离目标机动检测方法*
潘新祥,刘 凯
(1.海军驻连云港七一六所军事代表室,江苏 连云港 222061;2.中国船舶重工集团公司第七一六研究所,江苏 连云港 222061)
随着拖曳线列阵声纳在水下探测系统中的应用,水下作战平台的声探测范围成倍增大,甚至达到100km以上。因此在进行远程警戒、目标跟踪,甚至实施远程打击时,必然需要解决对目标的定位与跟踪问题,特别是在实际作战的对抗条件下,将不可避免地面对机动目标的定位与跟踪问题,其中的关键技术之一就是目标机动检测技术。
现有的机动检测技术大多将机动检测表示为二元假设检验问题[1-2]:

其中,u为机动量,m为机动起始时刻,在统计学中称之为变化点(change point)。所以机动检测问题与统计学中的变化点检测(change point detection)、变换检测(change detection)、突变检测(abrupt changes detection)相对应,这方面研究[3-4]已经成熟,其成果可以借鉴到机动检测应用中。
尽管目标机动检测研究已广泛引起学者们的兴趣,并在多个领域进行了成功应用,但在水下机动目标跟踪领域却极少提及。一方面对于水下目标而言[5],由于观测的数据率低、信息量少、误差大等特点,使得此类问题难度很大;另一方面由于水下系统的特殊性,公开发表的文献较少。针对水下探测纯方位机动目标定位与跟踪问题,文献[6-7]提出了用于纯方位量测的累积和目标机动检测与跟踪方法,文献[8]建立了纯方位机动目标定位与跟踪的体系框架。而纯方位远距离、大误差量测条件下的目标机动检测问题,难度更大,需要深入探索研究。
本文以拖曳线列阵声纳为探测信息源,首先在远距离(目标初距大于40km)、大误差(方位随机误差均方差大于2°)条件下,对通常的纯方位目标机动检测方法进行适用性分析,然后根据远距离态势的特点,提出一种新的目标机动检测方法,并通过仿真手段进行验证分析,最后给出验证结论。
1 纯方位目标机动检测原理
目标机动检测的任务是解决在目标发生机动后如何快速、准确地检测到此次机动。基于纯方位信息的目标机动检测,首先需要构造用于检测的统计量,然后利用各种统计检验方法检测出由于目标机动而引起的统计特征变化。在构造检测统计量时,简单地可分为两种方式:一是基于方位序列及其统计特征,利用变换、预测等手段,得到推算方位与实测方位的差值序列,从而构造出目标机动检测统计量;二是基于量测方位信息,在目标匀速直线运动假设条件下估计出目标运动参数,并利用该估计参数或其推算的方位序列的统计特征构造目标机动检测统计量。
拖线阵声纳在进行远距离目标探测时,主要量测信息为目标方位,且一般要求观测平台匀速直航。本文假定观测平台一直保持匀速直线运动,典型机动目标跟踪态势如图1。本文主要对常见的目标变向机动进行重点研究。

图1 机动目标跟踪态势示意图
因此,本文仿真实例中皆假定方位量测误差服从Gauss零均值独立分布,均方差为2.5°,方位采样周期1s,且固定目标初始方位为0°;为便于说明且不失一般性,选取典型态势为:目标初始距离60km,速度8.71m/s,航向150°,目标转向机动时航向变化率为1°/s;观测平台保持匀速直线运动,速度3.27m/s,航向90°。
2 纯方位目标机动检测方法与适用性分析
2.1 基于估计参数的方位预测误差累积和检测法
文献[6]通过对目标运动参数的估计进行方位的预测,得到方位预测误差序列{e(t)},从而构造出目标机动检测统计量。方位预测误差为方位的量测值与从滤波器中得到的方位的预测值之差。由k时刻的目标状态估计求k+1时刻的预测方位,并得到一步方位预测误差为


其中B(k+1)为k+1时刻的量测方位,(xo(k+1),yo(k+1))为k+1时刻本艇的位置坐标,为k+1时刻预测的目标位置坐标,其中
累积和(Cumulative Sum,CUSUM)检测[5]主要应用于信号处理领域,用来探测随机变量序列的均值变化。从对目标机动情况下典型的方位预测误差序列均值变化分析可知,当目标机动后,其均值发生了明显改变,见图2、图3。因此,可以将累积和检测原理应用于目标机动检测。

图2 目标匀速直线运动时方位预测误差曲线
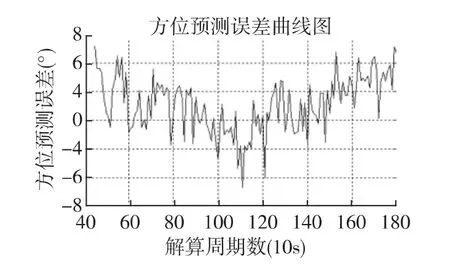
图3 目标在第90解算周期(900s)开始转向30°时方位预测误差曲线
假设方位预测误差序列{e(t)}是Gauss相互独立的,方差为σ2,其log似然比为sk,该似然比的累积和为Sk,则目标机动检测判决函数为

报警时刻:td=min{k:gk≥h}。
其中,h为设定的机动报警门限,该门限的选取可采用Monte Carlo方法统计得出。
2.2 基于方位变换的检测方法
本节将介绍不依赖于目标运动参数估计的机动检测方法,其使用的统计量仅为量测方位的变换函数值。
图4为目标与观测平台(单平台)的相对运动示意图。

图4 目标-观测平台相对运动示意图
设B(t)为t时刻目标的方位,当本艇与目标皆匀速直线运动时,则有:

其中,V为目标相对速度,Q0为目标的初始舷角,由式(1)可见当目标与观测平台均匀速直线运动时,目标方位随时间非线性变化。对式(3)转换得到:

即得到目标方位随时间线性变化的可量测函数。利用最小二乘方法对式(4)进行线性滤波,可得方位变换函数t·cot(B(t))的线性关系式。当目标发生转向机动时,理论上此种线性关系将被破坏,并由此检测出目标是否机动,见图5、图6。
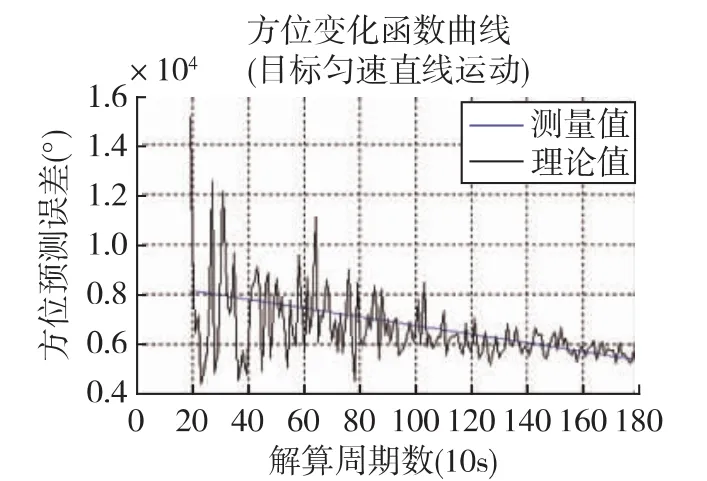
图5 目标匀速直线运动时方位变换函数值表征
2.3 远距离目标机动检测适用性分析
基于拖线阵声纳的纯方位远距离目标机动检测问题,有三个特点:1)目标方位量测误差大,误差均方差一般大于2°,甚至带有较大的系统误差,在利用方位预测误差序列作为统计量进行目标机动检测时,就很难区分量测误差与由目标机动所带来的预测误差;2)目标方位变化率小,不利于对目标运动参数的精确估计,难以基于估计的目标运动参数构造较平稳的机动检测统计量;3)在目标机动后,无论以何种方式构造的检测统计量的统计特征都是随时间变化的,并非发生急剧的阶跃变化。因此目标机动检测算法应当对很小的特征变化具有鲁棒性,即避免检测出由各种噪声引起的虚警机动,同时又要满足灵敏性要求,所以在实际应用中对算法的设计要求非常严格。
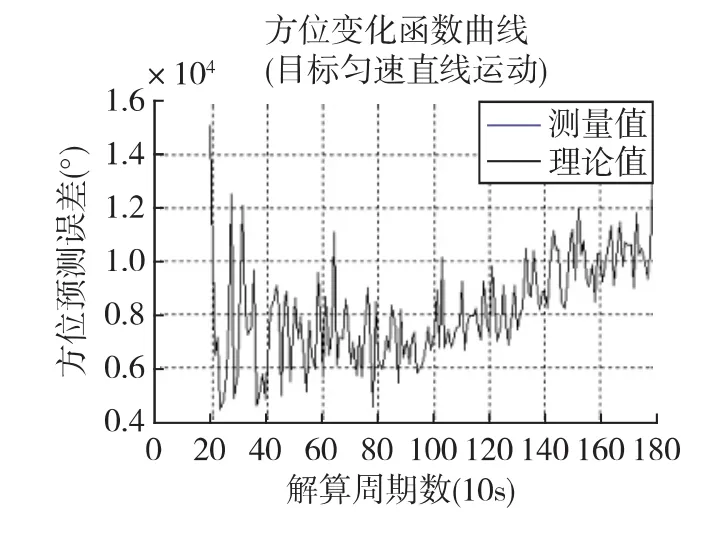
图6 目标在第90解算周期(900s)开始转向30°方位变换函数值表征
基于估计参数的方位预测误差累积和检测法所使用的统计量皆与估计的目标运动参数有关,其统计量表征的好坏依赖于匀直运动假设下目标的定位精度,而在远距离、大误差条件下,目标定位难度大,若定位算法的稳定度与精度皆不高,则该机动检测方法难以得到理想的效果。
基于方位变换的检测方法应用于基于拖线阵纯方位量测的目标机动检测时,由于目标距离远、方位量测误差大等因素,在初始相当长的一段时间内,方位变换函数值存在较大的波动(如图6),于是在机动检测时无法有效地控制虚警,此时适用性不太好。
为此,本文针对远距离目标方位变化的特点,提出一种基于方位线性预测的累积和机动检测方法。
3 基于方位线性预测的累积和机动检测方法
由上文分析可知,在远距离、大误差量测条件下,依赖于目标参数估计的检测方法和基于方位变换的方法都无较好的适用性。由于水下目标的速度低(一般小于16m/s),在远距离匀速直线运动时其方位二阶变化率相对较小,基本可以视方位序列为线性变化,见图7。
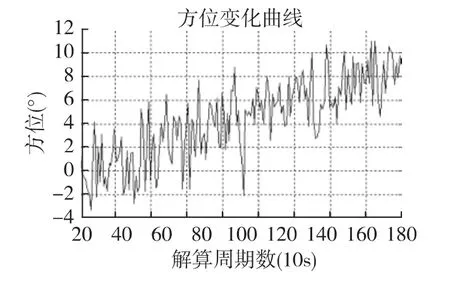
图7 目标匀速直线运动时方位序列表征
但是当目标机动后,方位的这种线性变化规律被破坏,并具有明显的表征,见图8。
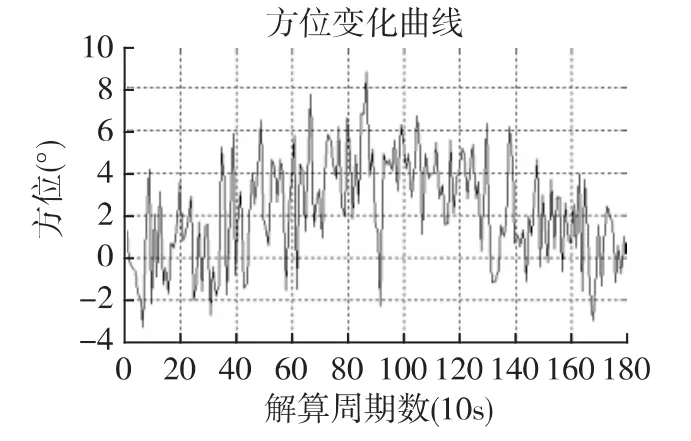
图8 目标在第90解算周期(900s)开始转向60°机动时方位序列表征
从图8中可见,在目标机动后,方位曲线的线性特征发生了明显的转折,并且方位-时间曲线仍具有近似线性特征。于是,可以采用对方位线性预测的方法构造用于机动检测的统计量。
假设在k时刻,对量测方位序列{B(i)},i=0,1…,k的线性拟合式为
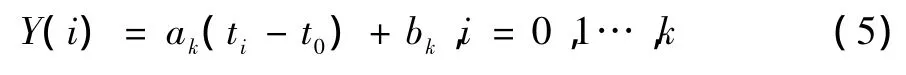
则利用此关系式进行m步预测,得到k+m时刻的预测方位为

k+m时刻的方位预测误差为

当目标匀速直线运动时,{e(k)}近似为零均值的序列,目标机动后其变化特征将发生明显的变化,见图9。然后利用上文中的累积和检测方法对序列{e(k)}进行目标机动检测。
在典型态势下,该方法得到的累积和检测量gk的表征见图10,图中目标在第90解算周期(900s)开始转向60°机动。
从图10中可看出,尽管图9中目标在机动后的方位线性预测误差变化趋势较缓慢,但在机动检测时得到的CUSUM曲线却发生了显著的变化。
此外,该方法由于方位线性假定的模型误差引起的机动检测虚警,可以通过调节设置的机动检测门限参数得到有效抑制。通过在不加量测噪声条件下对大量态势的仿真统计,上述原因引起的虚警率可抑制到几乎为0,并同时能够保证近乎100%的机动检测正确率。
4 仿真分析
本节将通过实验室仿真分析本文提出的目标机动检测方法的性能及特点。考察态势范围见表1。

图9 方位线性预测误差在不同情况下的表征

图10 累积和在目标机动时的表征
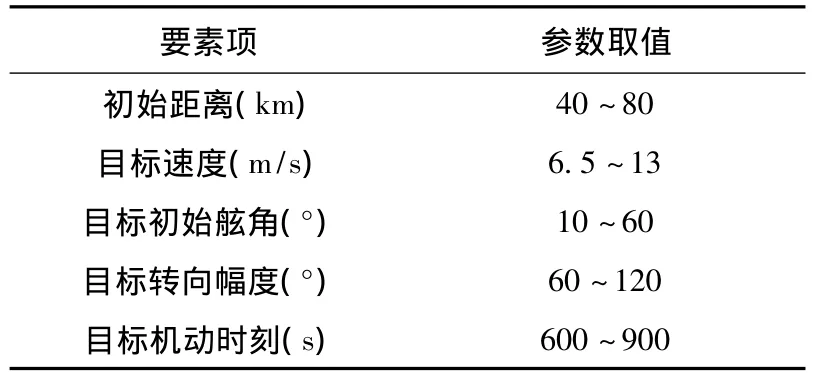
表1 仿真航路的参数选取
对每个态势进行100次Monte Carlo仿真,其中统计指标有:1)虚警率——目标保持匀速直线运动,即没有发生任何机动,但由于量测噪声的干扰等原因却检测到了“虚假机动”的概率;2)检测正确率——目标发生机动,且算法正确检测到此次目标机动的概率;3)检测反应时间——在正确检测出目标机动的条件下,目标机动检测报警时刻误差的均值。
为便于分析、比较,本文分别对在不同初距、机动转向幅度条件下的情况进行仿真结果统计,见表2、表3。
通过多态势的Monte Carlo仿真,结果表明本文提出的目标机动检测方法具有很好的稳健性:从表2、表3中仿真结果可看出,在实验室仿真条件下,目标机动检测虚警率小于1%,机动检测平均反应时间为180s左右,检测正确率近乎100%。比较表1、2的仿真结果统计值可看出,随着目标机动时刻的增大,机动检测效果稍有提高,但不明显。
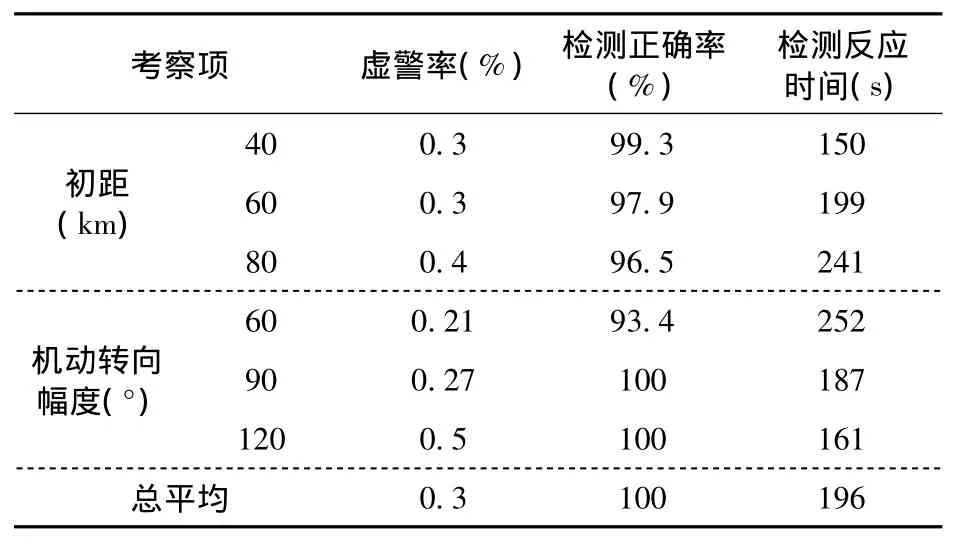
表2 目标600s时转向机动统计结果

表3 目标900s时转向机动统计结果
另外,随着目标距离增大,目标机动检测效果呈下降趋势,检测反应时间由150s增大至240s左右;随着目标机动转向的幅度增大,目标机动检测效果明显提高。
5 结束语
本文通过对基于拖线阵声纳的远距离、大误差条件下的目标方位序列的分析,结合信号处理领域的累积和检测理论,提出了基于方位序列线性预测的累积和机动检测模型。实验室仿真验证结果表明,算法对幅度稍大的目标转向机动,具有较灵敏的机动检测效果及较强的鲁棒性。
对于小幅变向或只变速机动目标,则由于在这些态势下用于检测的特征量皆无稳定的表征,导致检测效果大大降低。事实上,在远距离情况下,目标只做小幅变向机动可忽略,其对目前的定位算法效果影响较小。尽管在一般情况下水声目标多是变向伴随变速机动,只做变速机动情形较少,但仍需要进一步研究在远距离、大误差条件下的目标变速机动检测方法,以提高机动检测的实际适应能力。
[1]Ru J F,Jilkov V P,Li X R.,et al.Sequential Detection of Target Maneuvers[C].Proc.of 2005 7th International Conf.on Information Fusion,Philadelphia,PA,USA,pp.345-351,2005.
[2]Ru J F,Bashi A,Li X R.,et al.Performance Comparison of Target Maneuver Onset Detection Algorithms[C].Proc.of SPIE Conf.on Signal and Data Processing of Small Targets,vol.5428,2004.
[3]Lucas J.The Design and Use of V-Mask Control Schemes[J].JournalofQuality Technology, no 8, pp.1-12.1976.
[4]WaldA.SequentialAnalysis[M].Wiley, New York,1947.
[5]董志荣.舰艇指控系统的理论基础[M].北京:国防工业出版社,1995.
[6]刘凯,苗艳,袁富宇.用于纯方位机动目标跟踪的机动探测法[J].指挥控制与仿真,2006,28(2):30-34.
[7]孙世光,王炳,张国栋.一种基于满意滤波的纯方位目标跟踪算法[J].指挥控制与仿真,2012,34(6):51-54.
[8]陈霞,刘凯.水声目标机动检测与跟踪[J].指挥控制与仿真,2007,29(6):73-75.

