潜艇规避主动声纳浮标自主决策算法研究*

孙明太，秦 锋，陈遵银

(海军航空工程学院青岛校区，山东 青岛 266041)

航空反潜兵力使用被动声纳浮标或其它手段发现潜艇概略位置后，将使用主动声纳浮标进行搜索［1］，准确测定潜艇运动要素。而主动声纳浮标发出声波后，很容易被潜艇侦察并测定位置。此时，潜艇可以利用较高航速，尽快驶离主动声纳浮标的探测范围。

潜艇规避主动声纳浮标时，选择不易被声探测器材发现的深度，并采用最大的可用速度变向脱离。在速度受限情况下航向选择显得尤为重要。潜艇规避航向通常根据战场态势人工决定，具有盲目性，且延长潜艇的暴露时间。尤其是根据假定的一种或几种战场态势得出的规避措施不能满足作战仿真实验不确定性的要求。本文提出一种潜艇自主规避主动声纳浮标的决策算法，能够满足作战仿真实验中战场态势的多样性需求，为潜艇指挥员提供辅助参考。

1 潜艇自主规避决策算法

当潜艇发现主动声纳浮标时，规避航向的选取依赖于其发现的声纳浮标数量，以及确定的规避距离，潜艇自主规避主动声纳浮标的决策算法建立在笛卡尔坐标系基础上，具体分为以下3种情况。

1)当潜艇发现一枚主动声纳浮标。改变航向至主动声纳浮标径直相反方向，如图1所示。

图1 潜艇规避一枚主动浮标示意图

①根据探测到的浮标位置和潜艇实际位置，确定潜艇径直驶向浮标的航向H，航向H的确定与浮标所处的以潜艇为原点的坐标象限有关，具体如图2所示［2］。

图2 潜艇径直驶向浮标航向示意图

其中，(xq，yq)为潜艇的坐标，(xs，ys)为浮标的坐标。

②在航向H的基础上增加180°确定规避航向。

2)当潜艇发现两枚主动声纳浮标。通常当潜艇发现两枚主动非定向声纳浮标时，主动声纳浮标距离潜艇的位置有近有远。因此，首先潜艇按规避一枚浮标的方法逃离距离较远的浮标至B点，规避距离的选择要大于浮标声纳作用距离。再次，潜艇按规避一枚浮标的方法逃离距离较近的浮标至A点。两者逃离的距离是相等的，两者航路的向量和为潜艇的规避航向，如图3所示。

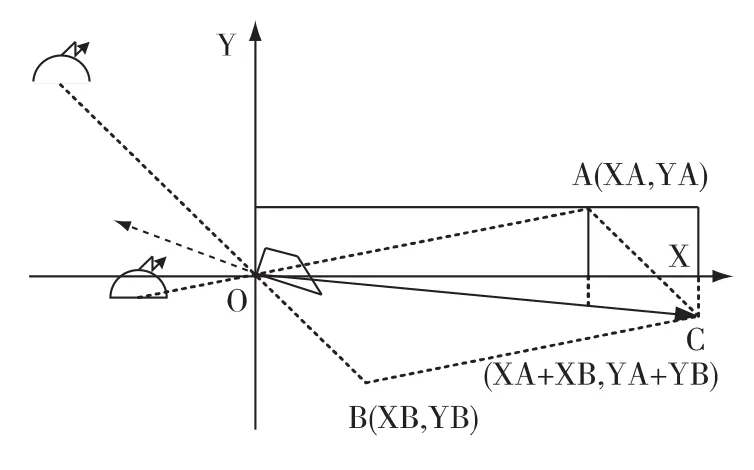
图3 潜艇规避两枚主动浮标示意图

①根据探测到的两枚浮标位置和潜艇实际位置，确定潜艇径直驶向两枚浮标的航向H1，H2;

②在航向H1，H2的基础上增加180°确定航向HA，HB;

③根据规避距离和潜艇至浮标的距离以及航向HA，HB，确定 A，B 坐标;

④根据A，B坐标确定C坐标，然后根据C坐标和潜艇实际位置，确定潜艇径直驶向C坐标的航向作为规避航向。

3)当潜艇发现三枚及以上的主动声纳浮标。规避航向的选择分为两种情况。

①若潜艇与各枚浮标夹角之和不等于360°，则不在浮标围成的三角形或多边形内，规避参考规避距离最近的两梅浮标，如图4(a)和(b)所示。这里要说明的是可能存在距离最近且距离潜艇位置相等的多枚浮标，这时从这些浮标中随机选取两枚浮标。

②若潜艇与各枚浮标夹角之和等于360°，则在浮标围成的三角形或多边形内，潜艇的规避航向平行于浮标与潜艇径向线夹角中最大角度的角平分线，如图5(a)和(b)所示。

还有一种特殊情况就是潜艇处于这几枚浮标围成的多边形边缘，则潜艇的规避航向恰好垂直于该边缘，如图6所示。

根据探测到的每枚浮标位置和潜艇实际位置，确定潜艇径直驶向每枚浮标的航向Hi。

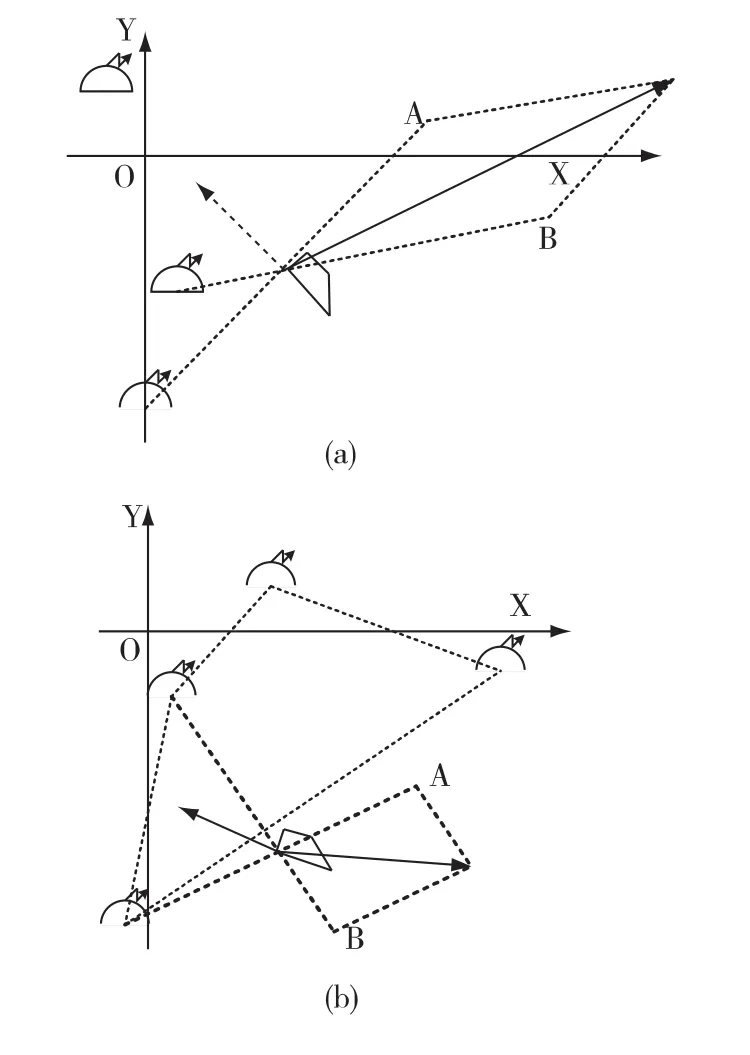
图4 潜艇规避三枚及以上主动浮标示意图(情况①)

图5 潜艇规避三枚及以上主动浮标示意图(情况②)

根据航向Hi，确定潜艇与每两枚浮标之间的夹角，若角度之和等于360°，则在浮标围成的三角形或多边形内，求取这些夹角中最大角度的角平分线作为规避航向。这里要说明的是可能存在多个相同的最大角度，求取这些角度的角平分线，再根据潜艇原先航向，选取转向差角最小的角平分线作为规避航向，如图7所示。若转向差角也一样时，随机选取角平分线作为规避航向，如图8所示。

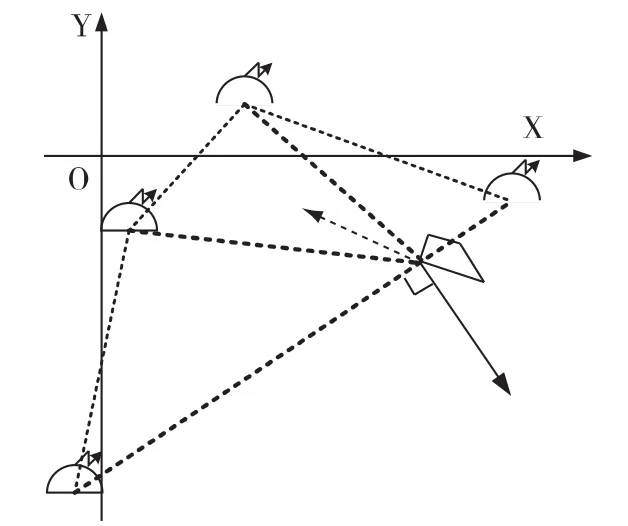
图6 潜艇规避航向垂直于边缘示意图

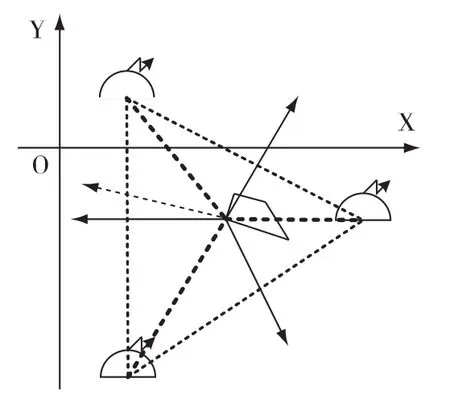
图7 角平分线规避航向示意图

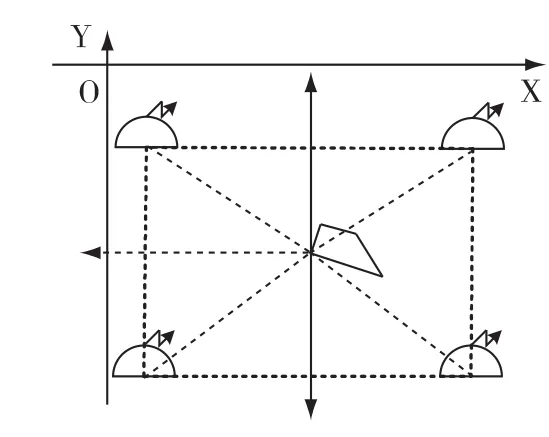
图8 随机角平分线规避航向示意图

若潜艇位置在浮标围成的三角形或多边形外围，从这些浮标中随机选取两枚浮标，按照发现两枚浮标的方法进行计算。

2 潜艇实体运动模型

由于潜艇对主动声纳浮标的探测，形成战场态势的感知，进而通过自主规避决策算法产生下一步行动的规划，因此有必要建立目标实体运动模型，模拟仿真潜艇作战行动过程中的实时位置和运动要素的变化，还原潜艇行动规划的物理过程。

2.1 速度变化模型

潜艇速度的变化规律满足指数函数条件。

增速时，速度从V0到VT的变化规律为

其中，a，b为增速参数。

减速时，速度从V0到VT的变化规律为

其中，Vt为瞬时速度，m/s;Kv为减速参数。

2.2 平面转向模型

潜艇是通过方向舵的作用实现航向的变化，航向随时间的变化过程为

其中，δ为舵角;K，T为动力系数;V0为初始速度，m/s。

仿真中取捷径转向至规定航向HT，因此有当H0＜HT＜H0+180°时，向右转向;否则反之。

2.3 平面运动模型

t时刻潜艇的二维位置为

其中，Δt为仿真步长，s;H为现时航向

3 仿真实例

3.1 想定

假设反潜飞机已知潜艇大概位置，布放如下图9所示的十字确认阵，由四枚主动全向浮标组成，当两到三枚浮标同时检测到潜艇时，测定其运动要素。其中，D为浮标间距，m。

图9 十字确认阵示意图

浮标位置为

此时，假定潜艇初始航向在0°～360°内满足均匀分布，初始航速在4kn～6kn内满足瑞利分布，初始位置在半径为2km的圆形区域内满足正态分布。在仿真过程中认为潜艇对浮标位置的探测定位存在一定的随机误差，在100m～200m内满足均匀分布。

在复杂的水声环境中，单枚浮标的探测范围不是一个圆形，其探测概率与距离的关系是一条波动的无规则曲线。但可以利用下面的指数函数代替 ，表现出探测概率随距离减小以及近距探测盲区的特性。同时确定检测概率为50%。

其中，r(t)为t时刻潜艇至浮标的距离，单位m。

图10 单枚浮标瞬时探测概率与距离关系

因此，整体浮标阵随时间变化的瞬时探测概率为

其中，n为浮标数量。

3.2 仿真及分析

根据如图11所示的仿真逻辑流程，利用蒙特卡洛法，设定模拟次数为2000次，十字阵浮标间距为1.4km。假定潜艇对主动声信号的侦察距离为3km，并在直航120s后发现浮标开始采用10kn速度进行自主规避。获取如图12—图16所示的仿真曲线示意图。其中，图12和图13为仿真过程中潜艇任意两次的规避航向和二维运动轨迹示意图。图14中虚线表示潜艇直航时十字阵的瞬时探测概率，实线表示潜艇自主规避时十字阵的瞬时探测概率。图15和图16虚线分别表示潜艇直航时十字阵两枚或三枚浮标可以同时检测到潜艇的瞬时概率，实线表示潜艇自主规避时十字阵两枚或三枚浮标可以同时检测到潜艇的瞬时概率。

由图14可以看出潜艇开始自主转向规避后，十字阵的瞬时探测概率得到明显的抑制，抑制程度的大小与采用的规避速度有关。

从图15和图16可以看出潜艇开始自主转向规避后，明显降低了被反潜机采用主动浮标定位跟踪和获取运动要素的机会。

图11 仿真流程示意图

图12 潜艇规避航向示意图

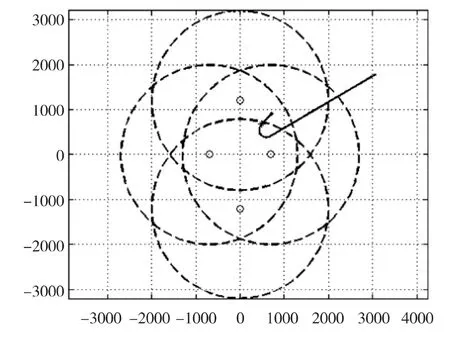
图13 潜艇规避航向示意图

图14 十字阵瞬时探测概率

图15 十字阵两枚浮标可定位概率

图16 十字阵三枚浮标可定位概率

4 结束语

反潜机使用主动声纳浮标可以实现对潜艇的精确定位，但潜艇可以感知并采取机动规避措施，如何有效降低被主动浮标发现的概率和暴露时间，是潜艇对抗反潜机的重要问题之一。本文提出潜艇自主规避主动声纳浮标的决策算法，并针对一型主动声纳浮标阵，在仿真分析探测概率变化规律的基础上验证了算法的有效性。该研究成果可以用作潜艇兵力CGF行动规划中的规避行为准则，使其具备基本的人工智能和自主行为，为潜艇作战指挥员对抗航空反潜搜索提供辅助决策，缩短其面对复杂战场态势下达作战命令的时间。

［1］孙明太.航空反潜战术［M］.北京:军事科学出版社，2003.

［2］Michael Shawn Wells.Implementation and Anlysis of a Smart Submarine in the Active Sonobuoy Model［R］.Naval Postgraduate School，September1991:15-22.

［3］M.P.Fewell，J.M.Thredgold ＆ D.J.Kershaw.Benefits of Sharing Detections for Networkedtrack Initiation in Anti-submarine Warfare［R］.Technical report DSTO-TR-2086 of the DefenceScience and Technology Organisation，June 2008:2-3.