一种无线电脉冲多普勒定高引信波束足迹仿真计算方法

王磊磊， 陈雨泽

（上海无线电设备研究所，上海200090）

0 引言

无线电脉冲多普勒定高引信兼具脉冲测距及多普勒测速功能，其目标为地面或海面。当导弹运行再入段过程中，引信的等多普勒线、等距离线以及波束线独立变化、相互重合，多普勒信号带宽也随之加宽，如何在极短时间内提取有效回波信号将直接影响定高引信的定高精度及导弹的毁伤效果，所以对其面目标回波进行动态仿真将十分重要。

1 定高引信雷达方程

定高引信是一种以地面或海面为目标的测高装置，与普通测距雷达的目标背景不同。定高引信有波束限制和脉宽限制两种工作模式。当天线波束覆盖范围不被等距离线（由脉冲宽度决定）分隔时为波束限制；当天线波束覆盖范围被等距离线分隔时为脉冲限制。

因为波束覆盖范围内的回波并不一定全是有效回波，所以需将雷达方程写成回波功率与有效照射面积的关系（式1），方可通用于两种工作模式。

引信天线发射功率为Pt，发射信号波长为λ，引信与地面的垂直高度H，天线增益为G，归一化雷达截面积σ0，照射面积为A，高度为H，则回波功率Pr为

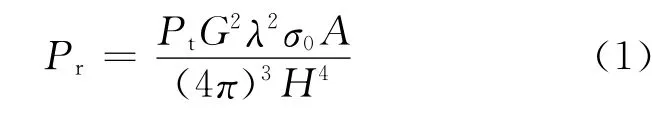
通常情况下，定高引信是工作在接近垂直入射的条件下，然而这种情况下的雷达截面积σ0的研究相对较少，但总的规律为σ0随雷达频率的增高而增大，随表面粗糙度增大而减小。

需要注意的是，近垂直入射时，σ0是天线波束宽度和距离的敏感函数。实际工程应用中，根据具体的应用条件引用文件资料中σ0数据［1］。另外，本文着重讨论等多普勒线、等距离线以及波束相互限制对目标检测的影响，回波起伏等问题不在本文的讨论范围内。

2 波束足迹

不失一般性，设天线俯仰面（E 面）波束宽度为θE，滚动面（H 面）宽度为θH，俯仰角为θ（-90°＜θ＜90°），滚动角为φ（-90°＜φ＜90°）。三维坐标系中，Y 正方向为导弹飞行方向，X 方向与Y 方向垂直，XY 面为水平面。不考虑俯仰角、滚动角（指波束垂直对地）时，收发共用天线坐标为（0，0，H）波束的立体方程为

考虑俯仰角为θ时，先将原波束按照向量（0，0，-H）平移，得

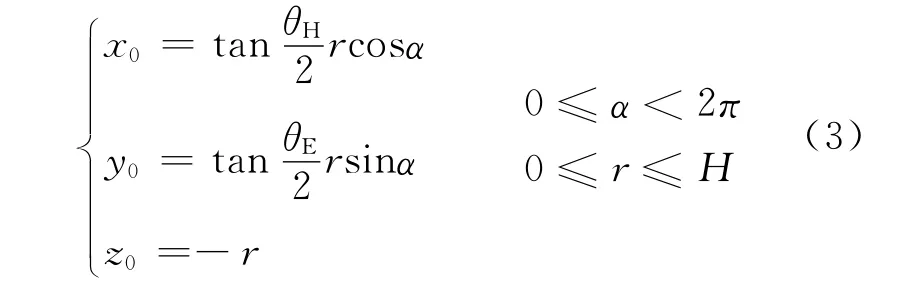
根据立体几何空间关系，以x 轴为中心，将波束按右手法则旋转θ

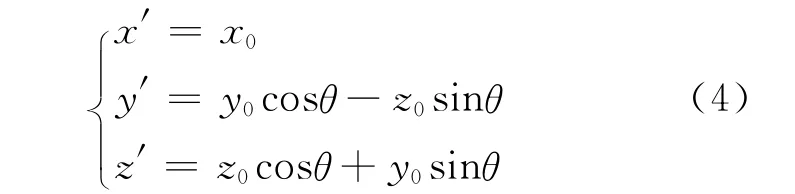
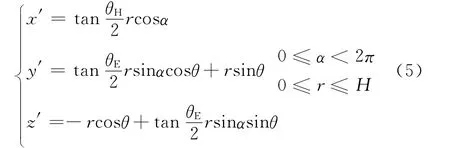
将式（1）代入式（2），滚动角为0°，俯仰角为θ的波束的立体方程为

以y 轴为中心，将波束按右手法则旋转φ，根据立体几何空间关系

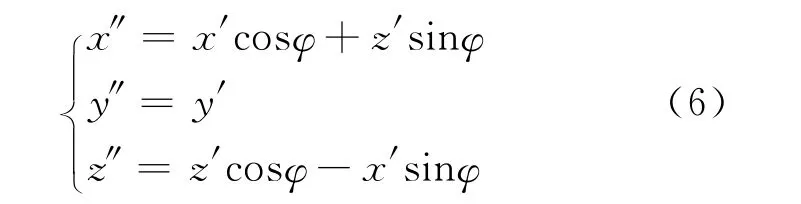
将式（4）代入式（5），滚动角为φ，俯仰角为θ的波束的立体方程为

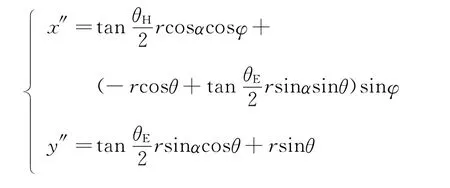
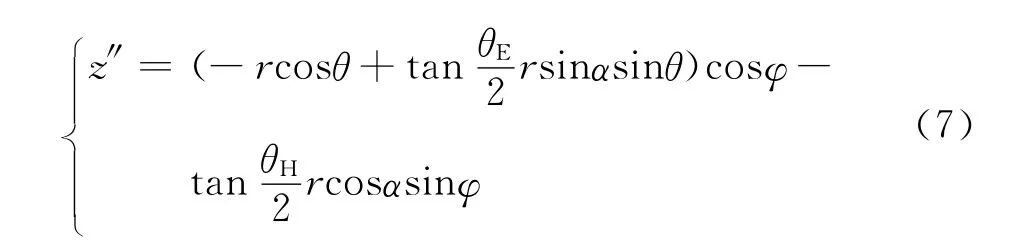
其中：

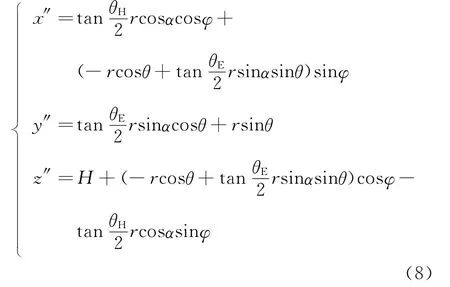
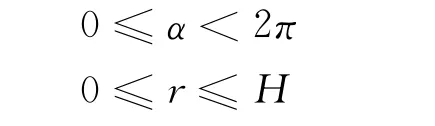
先将现波束按照向量（0，0，H）平移，得

根据式8，当z″＝0时

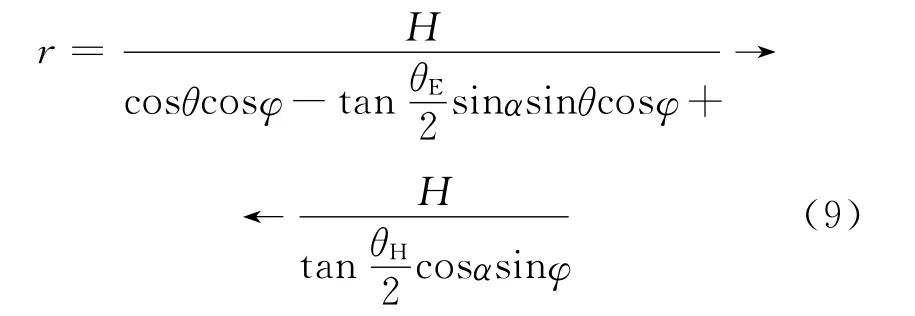
将式（9）代入式（8），可求出定高引信高度H，滚动角为φ，俯仰角为θ的波束足迹方程

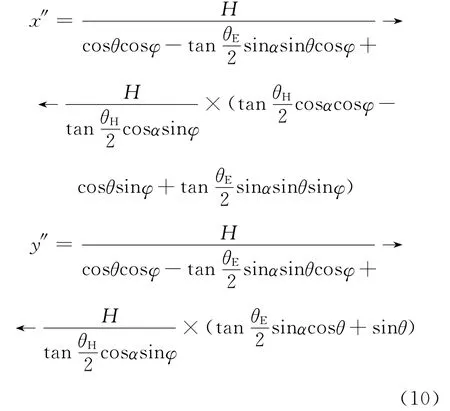
其中：

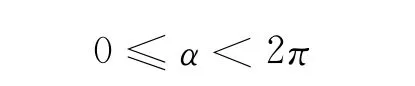
取 天 线E 面 波 束 宽 度θE＝30°，H 面 宽 度θH＝60°，俯仰角θ＝15°，滚动角φ＝15°，高度H＝60m，利用MATLAB三维画图工具［2］，波束三维图及波束足迹如图1所示。

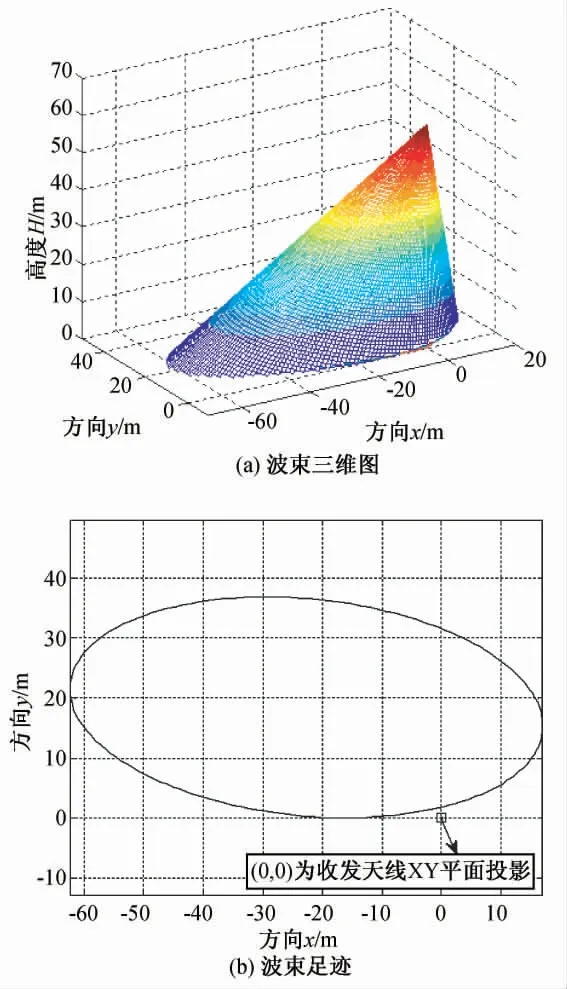
图1 波束三维图和波束足迹

根据波束足迹的方程可推导出面积方程，在此不作推导。

3 等多普勒线、等距离线、波束相互限制

脉冲多普勒定高引信实际工作时水平速度分量可以忽略，只考虑垂直速度分量即可。其等多普勒线和等距离线为两组同心圆。只有根据定高引信的具体工作情况，定量分析等多普勒线、等距离线、波束相互限制情况，才能制定出合理的信号检测判据。

不失一般性，设天线E 面波束宽度为θE，H面宽度为θH，俯仰角为θ（-90°＜θ＜90°），滚动角为φ（-90°＜φ＜90°），发射脉冲宽度为τ，电磁波空气中传播速度近似于光速c，多普勒分析带宽为Δf，垂直速度分量为v。

由发射脉冲宽度τ 可画出等距离线同心圆，由多普勒分析带宽Δf 可画出等多普勒线同心圆，如图2所示。

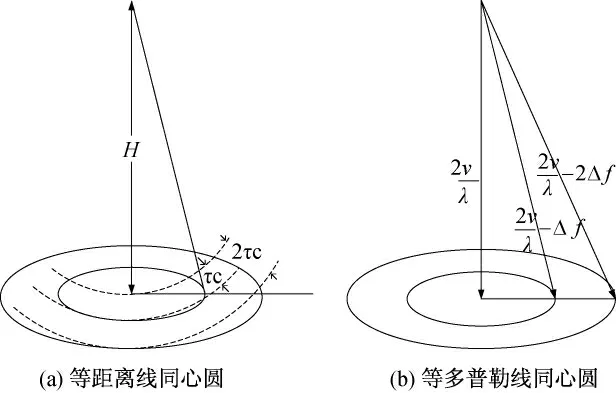
图2 等距离线与等多普勒线

如图3所示为此条件下等多普勒线、等距离线、波束相互限制情况，阴影部分为回波有效积分面积。

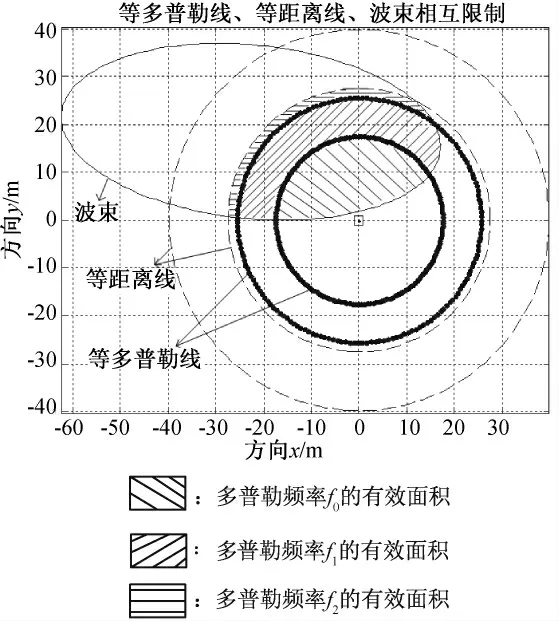
图3 等多普勒线、等距离线、波束相互限制

设天线E面波束宽度为θE＝30°，H面宽度为θH＝60°，俯仰角为θ＝15°，滚动角为φ＝15°，H＝60m，垂直速度分量为v＝1 000 m／s，λ＝0.02m，Δf＝4kHz。

地面回波经下变频、放大、视频检波、低通滤波后成为多普勒信号f。在图3的例子中，若装订高度为60m，当导弹逐渐进入装订高度直至移出的过程中［3］，f 所包含频率的基本变化规律为（f0）→（f0，f1）→（f0，f1，f2）→（f1，f2）→（f2）。使用FFT 进行多普勒信号检测时，频域上信号的主谱能量逐渐增大，带宽会逐渐展宽，最后带宽变窄，能量逐渐减小。

由此可以看出，制定信号检测判据时，不仅要对多普勒信号频率、能量进行判别，还要着重对多普勒信号主谱宽度进行分析。当然，通过装订高度对采样率进行适应性调整，可以灵活改变多普勒分析带宽，有利于增大多普勒信号频域峰值，但在实际工程运用中，过高的采样率不仅将提高数字信号处理机的实时性要求，且增加了设计难度。

4 结束语

本文在不考虑地形起伏的前提下，对定高引信波束足迹的数学方程进行推导。通过分析等多普勒线、等距离线、波束的相互限制，给出了脉冲多普勒定高引信面目标多普勒信号的基本变化规律。

如果进一步考虑回波起伏以及归一化雷达截面积随入射角的变化，可以大大增加回波仿真的置信度，并给实际运用提供较强的指导意义。

［1］ Merrill I.Skolnik.雷达手册［M］.北京：电子工业出版社，2003：485-490.

［2］ Bassem R.Mahafza，Atef Z.Elsherbeni雷达系统设计MATLAB 仿真［M］.北京：电子工业出版社，2009：360-401.

［3］ 潘荣霖，等.飞航导弹测高装置与伺服机构［M］.北京：宇航出版社，1993：198-249.