铍铜高速铣削表面粗糙度数学模型的构建*
□ 肖军民
中山职业技术学院 机械工程系 广东中山 528404
铍铜合金是一种可锻和可铸合金,属时效析出强化的铜基合金,经淬火时效处理后具有高的强度和硬度,并且稳定性好,具有耐腐蚀、耐磨、耐疲劳、无磁性和导热性好等一系列优点。由于铍铜材料诸多的优势,近年来铍铜应用在高端模具的比例也越来越大。铍铜模具的零件成型时间只有钢模的1/3~1/2,而铍铜模具寿命则可以达到钢模的5~6倍以上。随着我国制造业的转型升级,铍铜在高端精密模具的应用也将越来越广泛,因此研究和推广铍铜精密铣削加工技术对提高我国高端模具的制造水平具有重要作用。
表面粗糙度是衡量切削加工过程性能和评定零件表面质量的一个重要指标,它是切削系统中切削参数和系统变量对切削过程影响的综合反映,建立基于加工过程参数的表面粗糙度预测模型已受到国内外研究者的广泛关注。研究表面粗糙度目前有许多理论和方法,本文是基于正交切削试验法来研究铍铜表面粗糙度模型的。正交试验法是利用整齐的正交表来对试验进行整体设计、综合比较和统计分析,在因素变化范围内均衡抽样,以尽量少的试验次数找到影响因素中的主要问题,进而得出指导生产实践的正确结论。
1 数学模型的分析与研究
1.1 表面粗糙度的数学表达式

传统的切削表面粗糙度经验公式为:式中:K为切削条件综合系数;ap为轴向切削深度,mm;ae为径向切削宽度,mm;fz为每齿进给量,mm/z;v 为刀具切削线速度,m/min;Ci为待解系数。
该公式能较好地反映平铣刀切削平面工件的表面状态,但不能充分反映球形铣刀切削工件的表面质量。在球形铣刀等高切削工件的情况下,传统的表面粗糙度经验公式显然不能很好地反映加工表面质量。等高切削时,刀具每层下切深度对加工表面质量的影响是非常显著的,其次等高切削时切面处的锥角也将对表面粗糙度有较大影响,而这些在传统的经验公式中都没有体现。为了能更好地衡量球刀切削状态下工件表面质量的好坏,本文构建了式(2)所示的加工表面粗糙度模型:

式中:H为刀具每层下切深度,mm;A为刀具接触点曲面法向与刀轴的夹角,(°)。
1.2 表面粗糙度矩阵模型的建立
对于式(2)的指数方程进行数学求解是非常困难的,本文通过对式(2)两边取对数,将该指数方程转变为线性方程(3),然后再构建线性方程组进行求解,其过程如下:

令 b=lgRa,C0=lgK,x=lgv, y=lg fz, m=lgH, n=lgA, 则指数方程可转化为线性方程(3)。

式中:b、x、y、m 、n可以通过切削试验数据获得。
根据数学求解的必要条件,需要构建包含16个方程的方程组,因此构建如下的方程组(5)。而线性方程组(5)可用16阶的矩阵形式表达,如矩阵(6)所示。

上述矩阵(6)可简化为B=AC形式的矩阵,因此复杂的方程组就转变成了16阶矩阵的形式,方程组的求解也就转变成了对矩阵C的求解。要顺利求解出矩阵C中的每个数值,必须先要通过切削试验获得矩阵A、B中所有的数值,为此必须要设计相应的切削试验。
2 铣削试验条件
2.1 试件材料
试验用的工件材料为进口铍铜,牌号为C17200。铍铜的硬度为38~44HRC,抗拉强度为 1160~1380 MPa,密度为 8.3 g/cm3,热导率为 105 W/(m·K),其化学成分见表1。

表1 化学成分表
2.2 加工设备和测量仪器
数控机床采用中国台湾生产的双转台五轴联动加工中心,型号为HBCL1160H,最高转速可达30 000 r/min。铣削刀具采用直径为6 mm两刃TiAlN涂层的硬质合金球形铣刀。试验中采用SRT6200便携式表面粗糙度仪测量加工表面,该测量仪器的取样长度L可以根据测量需要进行选择,共有0.25、0.8、2.5 3个档次的取样长度。
2.3 试验方法
试验中采用顺铣和切削液冷却方式进行加工,刀具的切削轨迹为等高走刀模式,径向切削宽度为0.12 mm,采用UG8.0软件进行数控刀路的编制。
3 试验结果及分析
切削加工后测量试件的表面粗糙度,由于其测量具有不确定性,为减少测量误差,在此采用3次测量取平均值的方式,分别在试件3个标记处测量表面粗糙度,以3次测量的平均值作为该次加工后试件表面粗糙度的评定结果,表面粗糙度的测量结果见表2。
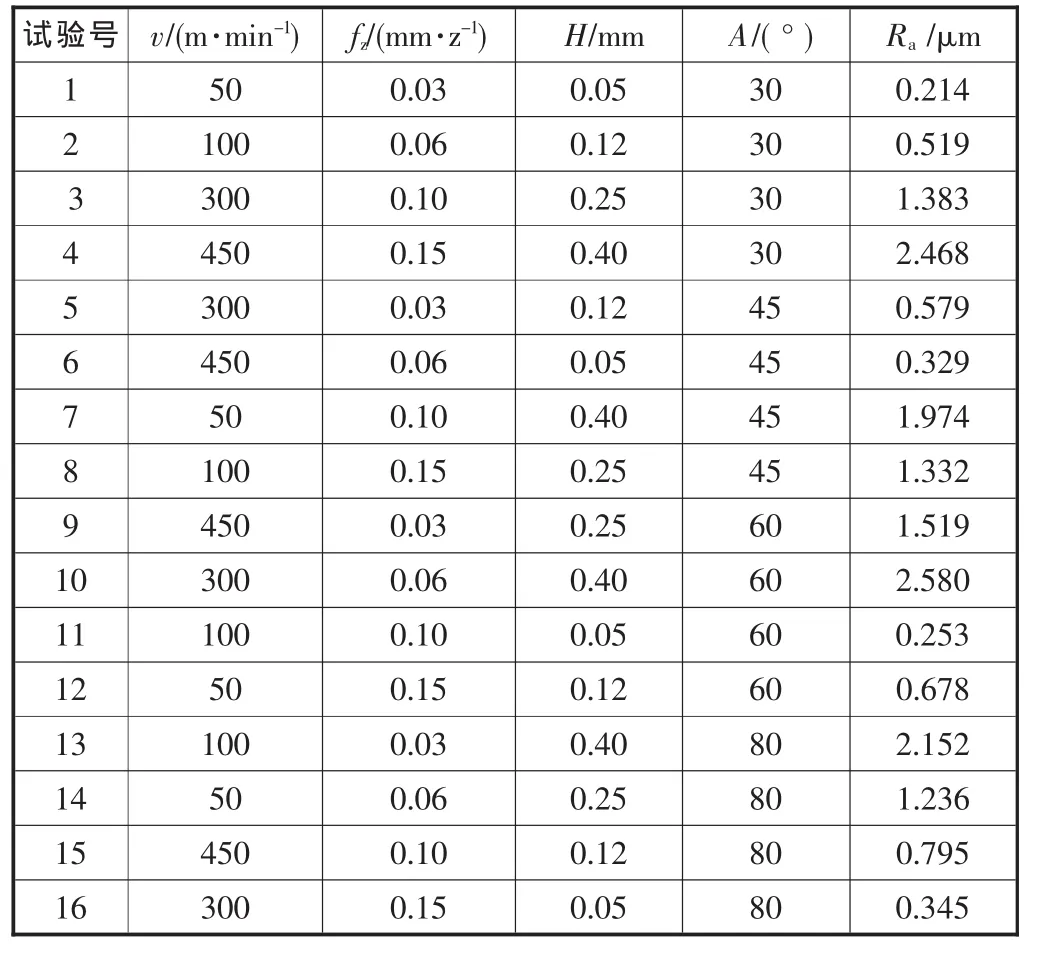
表2 表面粗糙度测量结果
4 表面粗糙度数学模型的求解
通过等式b=lgRa,可以求解出矩阵B中的16个数值,计算结果见表3。
通过等式 x= lgv、 y=lg fz、 m=lgH、 n=lgA, 可以求解出矩阵A中的64个数值,计算结果见表4。
矩阵等式B=AC,经过运算可以得到C=A-1B=A/B,虽然矩阵A和矩阵B都是已知的,但16阶矩阵的运算对于手工来讲是非常困难的。本文利用MATLAB软件进行求解,求解得到了矩阵C中的每个数值,具体结果见表5。利用表5中C0的数值可以计算得到切削综合系数K=1.93,并将表5中相应的数值代入式(2),则可得到铍铜等高切削模式下的表面粗糙度数学模型:
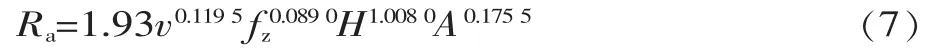
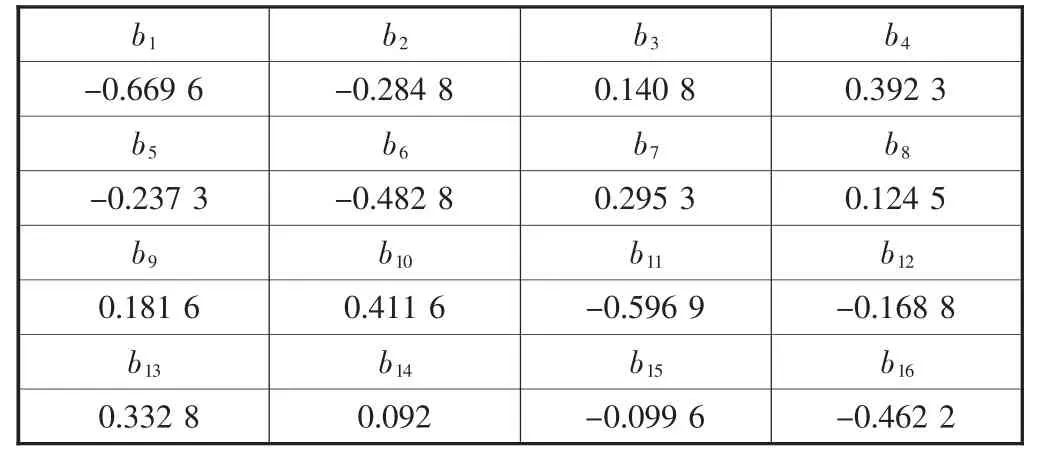
表3 矩阵B计算值
5 数学模型的约束条件和精度分析
铍铜加工表面粗糙度数学模型式(7)由于是依据试验数据获得的,所以在实际使用中必须要依据试验条件对该数学模型进行一定的约束。表面加工质量与数控铣削的切削方式有着密切的关系,结合本切削试验条件,给出该模型的约束条件①:切削方式要求为顺铣,走刀轨迹为等高方式。等高走刀模式不适合于浅平面的加工,因此给出该模型的约束条件②:刀具接触点曲面法向与刀轴的夹角A应大于等于30°。
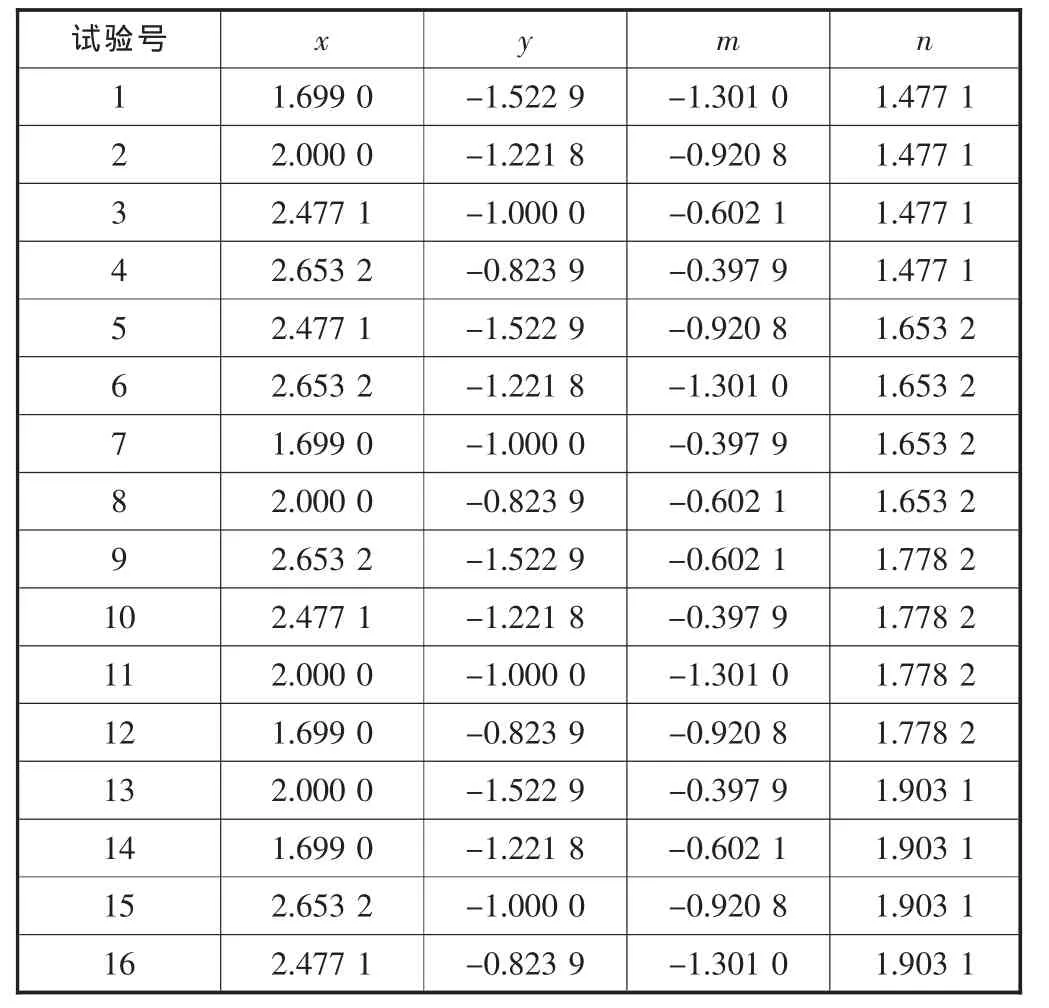
表4 矩阵A计算值

表5 矩阵C计算值
利用粗糙度数学模型式(7)对表2中的16组原始切削参数进行理论计算,并将计算的表面粗糙度理论值和表2中实测的表面粗糙度进行了比较。比较的结果如下:最大误差出现在试验号为5的试验数据中,误差率为11.0%;最小误差出现在试验号为2的试验数据中,误差率为0.9%。
6 结束语
机械加工表面质量的分析、控制和仿真是工业纹理分析的一个重要方面,建立机械加工表面质量的模拟模型,不仅可为虚拟制造创造条件,为表面性能分析奠定基础,也可为优化机械加工参数提供重要参考。本文通过分析等高铣削模式下铍铜表面粗糙度影响因素的特点,提出了表面粗糙度仿真模型,利用正交切削试验数据和MATLAB软件推导并求解出了铍铜表面粗糙度数学模型。该模型是基于工艺参数建立的,且精度能控制在10%左右,因此可以用来优化实际的切削参数,从而在保证加工质量的情况下提高铍铜模具成型零件的生产效率。
[1] 胡知音,孟广耀,夏海涛.基于正交试验法的GH4169高速铣削表面粗糙度研究 [J].制造技术与机床,2011(1):44-46.
[2] 杨济森,郭宏伟,李洪涛.航空铝7050高速铣削表面粗糙度试验研究 [J].机械制造与自动化,2011(7):34-35.
[3] 刘牧,杨茂奎,霍颖.复杂曲面五坐标数控铣削表面粗糙度预测的关键技术研究 [J].机械制造,2005(11):12-14.
[4] 郭秀华,陈祥林.基于高速铣削铝合金6061表面粗糙度试验研究 [J].机床与液压,2011(3):38-39.
[5] 张永顺,孙华,丁伟,等.基于BP神经网络的切削表面粗糙度预测方法[J].机械管理开发,2011(10):71-74.
[6] 张斌.数控加工表面粗糙度的预测 [D].西安:西北工业大学,2007.
[7] 陈惠贤,冯海涛,杨富强,等.2Cr13不锈钢高速铣削表面粗糙度预测模型研究 [J].工具技术,2012(2):73-76.
[8] 鄢国洪,张华贵,刘浩.侧铣削参数对TC4钛合金表面粗糙度影响的试验研究 [J].机械制造,2011(9):72-75.

