VC++与Matlab混合编程技术在 现代控制理论系统仿真中的应用

一、引言

现代控制理论是建立在状态空间基础上的一种控制理论，是自动控制理论的一个主要组成部分。在现代控制理论中，包括线性系统和非线性系统，定常系统和时变系统，单变量系统和多变量系统，它们在建模之后都表达为矩阵形式，因此通过计算机进行控制系统的仿真，实质就是利用计算机来进行矩阵运算。小型控制系统进行仿真时，所涉及的控制算法以及矩阵运算量都是有限的，因此对仿真的效能要求较低。而当需要进行复杂系统的仿真试验时，不仅编写相应的控制算法消耗大量的人力，较低的程序执行效率也将消耗大量的计算机运算能力，因此选取和使用快捷高效的仿真开发方法显得尤其必要。

Matlab是一种应用广泛的数学类科技应用软件，在数值运算尤其是矩阵运算方面有着非常好的表现，用户不需要深刻了解算法及编程技巧，只需掌握了入门的数学知识和程序设计能力就可以利用其进行复杂的科学计算，如今已经成为学界理论分析和实验研究所必须掌握的软件工具之一。但限于其本身是一种解释方式运行的高级计算机语言，在进行重复计算工作时执行效率较低，且运算过程不能脱离计算机环境进行。VC++是微软公司推出的开发环境Visual Studio中的一个组成部分，用户可以利用其进行快速的Windows应用程序开发，设计出图形界面丰富的功能软件，但是在编写矩阵运算时缺少专业的数据类型变量，当编写复杂的算法时不免要消耗大量的编程时间[1][2]。

比较两者的优缺点后不难发现，Matlab易于使用但是在仿真时程序运行效率低[3]，实时性较差，使用条件有限，VC++不便于直接进行矩阵计算但是代码运行效率高，实时性较好，应用范围广，也就是说，如果通过混合编程能让两者的优势互补，在工作中将大大减少在算法编程方面的工作量，并且能够改善仿真程序代码的运行效率以及实时性，为科研工作和工程开发提供更强大的技术支持。

二、混合编程方法简介

目前VC++与Matlab相结合的混合编程主要有以下几种方法[4]：

1.在VC++中调用Matlab引擎（Engine）

这种处理方法不要求链接整个Matlab，只需嵌入必要的Matlab引擎库，节省了大量的系统资源，使应用程序整体性能更好，处理效率更高，但这种混合编程的方法需要Matlab在后台适时运行不能脱离Matlab环境，严重影响了程序的通用性，因此这种方法在实际开发过程中很少采用。

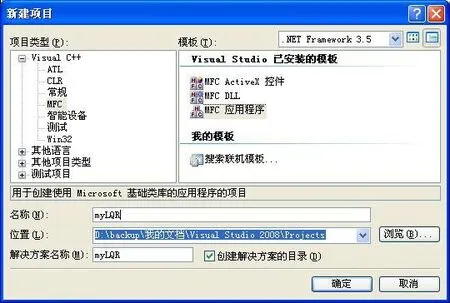
图1 新建 VC++对话框程序

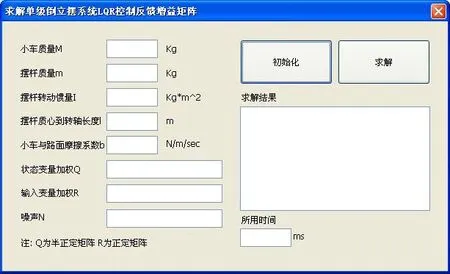
图2 设计程序界面

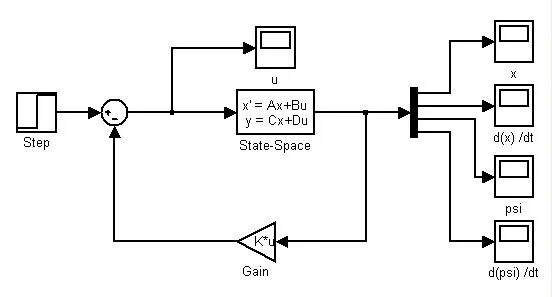
图3 单级倒立摆系统仿真框图

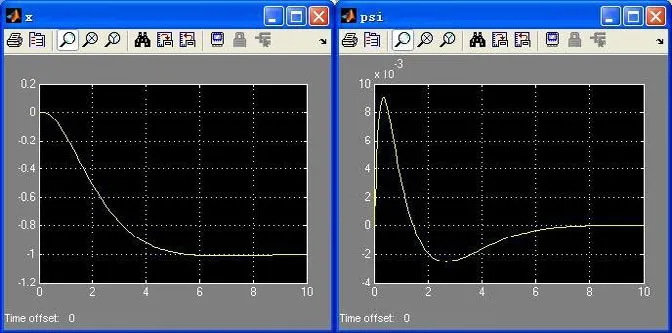
图4 Simulink仿真模型得到的仿真结果

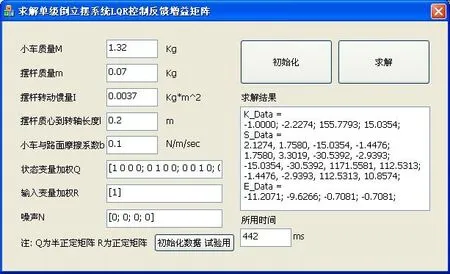
图5在VC++中求解反馈增益 矩阵 K

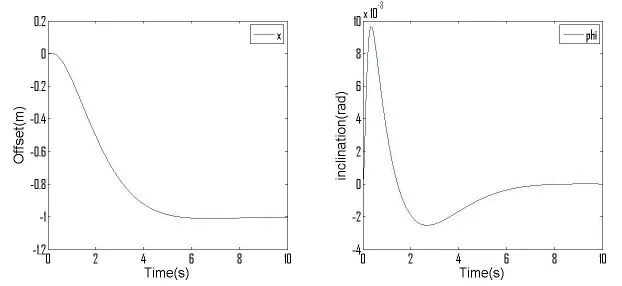
图6 根据VC++中求得的增益矩阵K得到的仿真结果

图7 Matlab中求解增益矩阵K消耗 的时间

图8 VC++中求解增益矩阵K消耗的时间的方法

2.Matlab调用由C/C++编写编译为mex文件的函数

这种方法是对Matlab函数库和一种补充，用户可以自已编写一些高效或者具有特定功能的函数，利用编译器把它们编译为mex文件，供Matlab调用，相当于添加自定义的Matlab函数。

3.在VC++中调用Matlab生成的动态链接库

这种方法通过指定的编译器，把由Matlab编写的m函数文件编译成动态链接库文件（dll）。只需在程序开发和发布中包含其生成的动态库，就可以在VC++程序中调用封装好的Matlab函数，实现数值算法的运用。这种方法可以使程序脱离Matlab运行环境，减少文件外部存储空间的占有量，并实现了代码共享。

4.使用COM组件对象模型技术实现混合编程

COM技术是一种应用广泛、方便灵活的方法，是利用Matlab提供的Deploy Tool工具实现Matlab与C/C++的混合编程。COM给软件开发人员提供了一种共享二进制代码的方法，但是由于缺乏可视化界面，其应用范 围受到一定限制。

三、混合编程实例与验证

从实际应用角度考虑，前两种编程方法虽然简便，但适用范围狭窄，第四种方法适用性好于前两种方法，但需要用户掌握较高的程序设计水平，不便于科研人员使用。本文选用第三种方法进行编程，并以控制工程中经典的单级倒立摆系统的LQR线性二次型调节器的设计为例，描述这一方法的实现过程，验证其在控制系统仿真中能够带来的优势之处。

本文所采用的软件版本是Visual Studio 2008和Matlab R2010a。

1.混合编程步骤

(1)Matlab编译环境的设置

控制算法从Matlab到VC++的代码转制要通过编译器来进行，所以首先要设置Matlab的编译环境。启动Matlab R2010a，在命令窗口中输入命令mbuildsetup，根据出现的提示选择合适的编译器，本文所使用的是Microsoft Visual C++ 2008。

(2)编写包含函数算法的m文件并且进行编译

本例中m文件实现了单级倒立摆系统矩阵x˙= A x+ B u 和LQR控制反馈增益矩阵的函数fu nction[K,S,E]=myLQR(Info,Q,R,N)的求解过程。这里需要说明的是，m文件应是函数的实现而不是单纯的脚本文件，而且从混合编程的角度来讲，编译脚本文件不具备实际意义。

Matlab提供了三种使用Matlab编译器的方式[5]：①在Matlab环境中使用mcc命令；②在系统命令环境中使用mcc.exe(在Windows上)；③在Matlab环境中使用Deployment Tool。

以第①种方法为例，m文件编写完成后，在Matlab中修改当前工作文件夹路径为包含m文件的文件夹路径。在Matlab命令窗口中输入：mcc- W cpplib:myLQR-T link:lib m yLQR.m即可将m文件编译为动态链接库文件。

(3)建立VC++工程并进行属性设置

新建一个空白的对话框工程。

如图1所示，在项目-属性-配置属性-C/C++的附加包含目录中加入”MATLAB PATHR2010aexterninclude”，其中MATLAB PATH是Matlab在硬盘中的安装路径。

在项目-属性-配置属性-链接器的附加库目录中加入”MATLAB PATHR2010aexternlibwin32microsoft”。

在项目-属性-配置属性-链接器-输入的附加依赖项中加入”mclmcrrt.lib myLQR.lib”。

将上一步中由m文件生成的头文件、动态链接库文件和静态链接库复制到VC++工程文件夹目录下。

(4)VC++界面设计及数据接口编程

根据单级倒立摆的基本参数，以及LQR线性二次型调节器的加权参数，设计VC++对话框的图形界面，并使用mwArray类型变量配置动态链接库函数的数据接口，如图2所示。

2.验证编程有效性与运行速度

(1)Matlab中的运算结果

在Simulink中依据单级倒立摆的系统仿真框图建立仿真程序模型，如图3所示。

选取一组适当的单级倒立摆系统参数[6]。

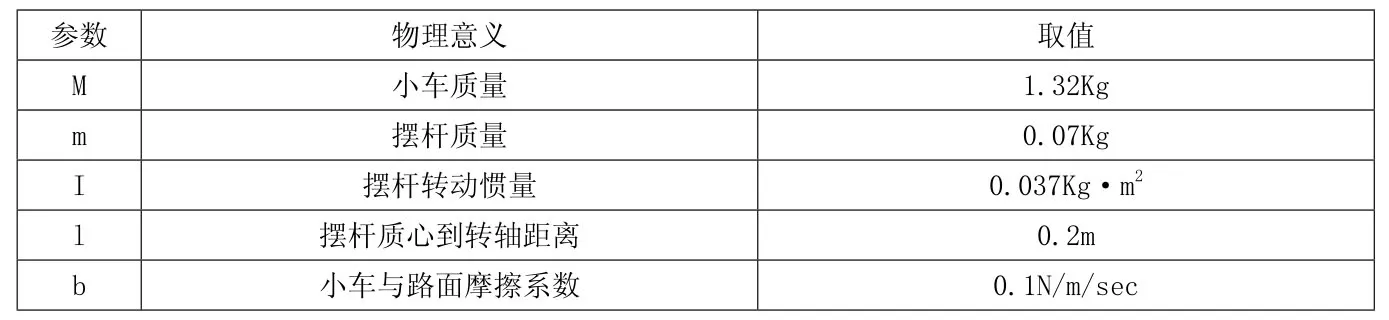
表1 单级倒立摆系统参数

根据单级倒立摆系统的系统模型[7]。

将得到 的最优反馈增益矩阵K加到Simulink仿真模型中的反馈增益环节上。仿真后得到输出结果为小车位移x和摆杆倾角Ψ，如图图4所示。

(2)VC++中的运算结果

在求解LQR二次型最优控制反馈增益矩阵的程序中输入与 前文中单级倒立摆系统相同的系统参量，并进行计 算，得到最佳反馈增益矩阵K，如图5所示。

选择时间轴T=0:0.005:10，使用lsim命令可以求得此单级倒立摆系统的输出响应分别为小车位移x和摆杆倾角Ψ，如图6所示。

对比两次仿真的结果可以得出结论，利用编译器编译m文件得到的动态链接库文件所包含的函数能够正确进行矩阵运算，得到LQR二次型最优控制反馈增益矩阵K。

在Matlab中使用其自带的Profiler工具统计myLQR函数求解反馈增益矩阵K时所消耗的时间为5 14毫秒如图7所示。

而在VC++中，在调用myLQR函数的语句前后分别使用GetTickCount（）函数查询当前系统时间，两次查询的结果作差后，即得到VC++执行函数myLQR求解矩阵K所消耗的运算时间，如图8所示。

程序运行后得到VC++中调用myLQR函数消耗时间为442毫秒，如前文图5所示。说明了在进行相同的矩阵运算时，VC++环境下具有略优于Matlab环境下的代码运行效率。

四、结论

可以看到，通过使用混合编程技术把Matlab中有关于控制算法的函数转编为VC++可用的动态链接库形式，在用户没有进行任何控制算法编写的情况下，就可以完成在VC++中对控制系统的控制变量的求解，进而完成控制系统仿真。免去了用户需要亲自编写C/C++控制算法的繁琐工序，只需用户编写一部分接口程序即可，而且通过单级倒立摆系统最优控制反馈增益矩阵的求解实例还可以论证，这种编程方法集成了两个软件的优点，使得生成的程序同时具备较好的运行效率和实时性、普适性，拓展了Matlab在现代控制理论系统仿真中的适用范围，有助于缩减新型控制算法的编程周期，为新型控制算法的研究与开发提供了一种新的编程思路。

[1]张亮,王继阳.MATLAB与C/C++混合编程[M].人民邮电出版社,2008.

[2]刘维.精通Matlab与C/C++混合程序设计(第二版)[M].北京航空航天大学出版社,2006.

[3]李曦,唐琳.在MATLAB中运行其他可执行软件的方法[J].微计算机信息,2006,22(3-3).

[4]杨刚,姚华.实用航空发动机LQR权阵选取方法[J].南京航空航天大学学报,2006(4).

[5]Robin G.Qiu and Yongfeng Ju Research on MATLAB Programming Efficiency.Mei Xiao et al.,2011,Applied Mechanics and Materials,135-136,788.

[6]BaiLi Zhang,JiangGuo Wang,The Analysis and Simulation of First-Order Inverted Pendulum Control System Based on LQR.ISIP2010 Third International Symposium.

[7]Hongliang Wang,Haobin Dong,Lianghua He,etc.Design and Simulation of LQR Controller with the Linear Inverted Pendulum,ICECE2010 International Conference.

[8]Shiyong Yang,Liping Xu,Peijin Wang.“Study on PID Control of a Single Inverted Pendulum System”vol.S1,2007.