高精度全站仪在涟水特大桥二等跨河水准中的应用分析
(铁道第三勘察设计院集团有限公司,天津 300251)
1 工程概况
长昆客运专线涟水特大桥位于湖南省湘乡市水府庙库尾,全长756.42 m,桥址区内局部地段高差相对较大,坡度较陡,树林密集,通视情况不好;涟水河为常流性水体,水面距离在300~600 m,水深3 m,最大流速为4 m/s;大桥小里程河岸为河滩,地形平缓,过200 m为河堤,河堤到水面高度15 m,大里程距水面20 m为河堤,河堤至水面高度10 m。
2 跨河水准测量方案
结合现场的具体地貌进行跨河点布置,选择在涟河特大桥上游50 m(狭窄处)进行跨河测量,在两岸河堤上布设四个跨河点A、B、C、D,构成四边形,同岸近距点间距约为10 m,对岸的远距点约为600 m,从图1可以看出,跨河点构成的四边形ABCD有6条边,组成3个独立的闭合环。
外业观测按图2顺序进行,河两岸分别架设2台Leica TCA2003全站仪、两部定长棱镜脚架(免量仪器高),使用对讲机协调确保对向观测同步,使用TCA2003的ATR自动照准和机载多测回测角软件,按照测回法获取对岸点间高差hBC、hBD、hAC、hAD,同岸点hAB、hCD使用Leica DNA03电子水平仪观测。

图1 跨河水准布置示意
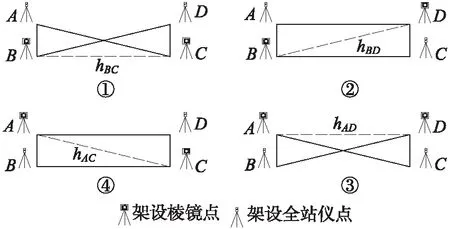
图2 全站仪跨河对向观测顺序
3 跨河水准测量的精度估计
对全站仪对向观测高差误差来源及大小进行分析,主要有:垂直角观测误差,测距误差,大气垂直折光差,仪器高、目标高的量取误差和垂线偏差。由误差传播定理,可推得其观测高差中误差的计算公式为
(1)
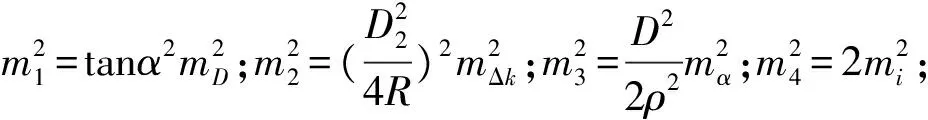
(2)
由公式(1)可知,m1、m2、m3、m4即为影响三角高程测量精度的主要因素,分别为:测距误差、球气差、测角误差、量高误差。D远距点≈600 m,D近距点≈10 m,同岸点误差可忽略。两岸河堤高差为5 m,推算竖直角为0.48°,取α=0.5°,mΔk=±0.01,Leica TCA2003全站仪方向观测精度为0.5″,mα=±0.5″,电子度盘的最小分辨率为0.1″,测距精度ms=1 mm+10-6×D;全站仪对向观测消除了仪器高的量取误差,棱镜架使用定长装置免除了棱镜高量取误差;将上述各值代入公式(2),各项测量误差见表1。

表1 三角高程跨河水准高差精度估计 mm
从表1可以看出,由精密误差公式推导近似误差计算公式时,使用高精度全站仪和定长装置,可忽略影响较小的误差,并消除量高误差。结合实际情况,估算各参数在不同取值的情况下mh的取值情况。现取α=1°,S=100 m,200 m,300 m,…,1 000 m代入公式(2),分别计算测距误差m1、球气差m2、测角误差m3及对向观测高差中误差mh,见图3。
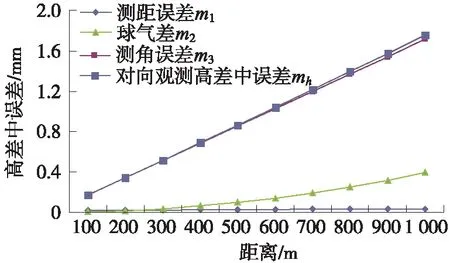
图3 跨河水准高差各项误差与跨河距离的关系
从图3可以看出,随着跨河长度的增加,高差中误差急剧增大。因此,在条件允许的情况下,尽可能选河道较窄处缩短跨河视线长度;高差误差的主要来源是测角误差和大气折光差(球气差),使用高精度全站仪来提高测角精度,选择好天气和采用同时对向观测来减弱大气折光误差。
4 观测结果及数据分析
对TCA2003全站仪对向观测的四组自动观测数据进行整理,各项指标均均满足要求(见表2)。同岸点间高差使用电子水平仪往返观测hAB=0.101 5 m、hCD=0.058 2 m,各点间实测水准高差如图4所示。由于AB、CD距离较近,hAB、hCD、数值当作已知值,按照条件平差的原理对跨河水准网进行严密平差,6个观测值,3个多余观测,采用Helmert方差分量估计法,整个跨河水准网构成3个条件方程式,并对之进行精度计算。

表2 各跨河点间三角高程高差统计情况 m

图4 跨河点高差示意
平差过程及结果如下:
条件方程式为
VhBC-VhAC+1.0=0-△ABC
VhBD-VhAD-1.9=0-△ABD
VhBC-VhBD+1.5=0-△BCD
法方程为
(3)
平差结果为
从各跨河点间的高差改正数可以推算得到B、C点间三角高程高差hBC,并按二等水准检测B、C点几何水准高差;按照公式(1)和严密平差分别计算理论测高中误差和实际测高中误差(见表3)。可看出,三角高程理论测高中误差和由严密平差得到的高差中误差基本相等,其精度达到二等水准的要求。

表3 几何水准高差与三角高程高差对比分析
5 结束语
采用高精度全站仪对向观测进行跨河二等水准测量精度良好,能满足客运专线精密控制测量高程控制网的要求,其测高主要误差为测距误差、球气差、测角误差。通过该项目,体会到二等跨河水准测量有以下几方面关键点:
①布置跨河点位置要保证两岸跨河点高差不应相差太大。
②采用定长杆连接棱镜消除量高误差对提高跨河水准精度有很大意义。
③测角误差是全站仪三角高程跨河水准测量的主要误差源,要尽可能的采用高精度带ATR自动照准功能的全站仪进行多测回观测。
④由于多余观测量少,建议采用多期观测,增强跨河水准网图形条件,通过Helmert方差分量估计提高测量精度。
[1]GB/T 12897—2006国家一、二等水准测量规范[S]
[2]李付伟,高淑照,刘成龙,等.ATR技术在杭州湾跨海大桥跨海三角高程测量中的应用[J].桥梁建设,2006(6).
[3]刘忠林,薛维刚.精密跨河水准测量方法与数据处理[J].测绘与空间信息,2009(4)
[4]范百兴,李广云.Helmert方差分量估计在跨河水准测量中的应用[J].测绘学院学报,2004(1)

