基于旋转对称轴的从不完全点云提取骨架的算法研究

段红娟 （湛江师范学院基础教育学院，广东 湛江524037）

一个图形的骨架，特别是像人或者其他带关节的动物的形状，给人直觉的和深刻的抽象，能够方便的理解和控制形状。最出名的骨骼表示为Blum中心对称轴［1］，与它相关的变量一起作为通用表示，用来获取形状内部的反射对称。三维模型的中心对称轴一般是包含二维表单的非流形，难以存储和熟练操控。另一方面来说，由于其拓扑结构简单，使得计算效率高并且容易操控，一维曲线骨架在实践中更有用。

现存的大多数曲线骨架提取算法主要处理用闭合多边形表示的形状。虽然从点云数据中估算曲线骨架是可行的，如通过从输入云 “内部”产生的可变形团，或者依赖于点集的Voronoi图表。但是迄今没有一种方法用来处理丢失了大量重要数据的点云。不完整数据大多由激光扫描造成，源于物体的自遮挡或者表面材质不够理想条件，这类问题在实时捕获运动对象的时候更加普遍。由于相机取景非常有限，未经加工的点云包含了大量空洞和严重欠采样。为此，笔者提出了基于旋转对称轴的从不完全点云中提取曲线骨架的算法。

1 三维模型曲线骨架及提取技术

1．1 三维模型曲线骨架

骨架作为形状表示的一种有效形式，在几何分析及相关处理中，有着非常广泛的应用。骨架能够代表模型的拓扑结构和关键形体特征，是模型的拓扑抽象表示。Blum 1967年给出了骨架的最初定义：骨架 （中轴）是模型内部各个最大内切球中心的集合。它还有一个模拟定义，即从模型表面开始点火，各个方向上的火的相遇点所构成的集合。

在CAD中提取模型的曲线骨架，可以利用已存在的模型，进行再加工编辑和处理，产生新的模型；在计算机动画制作产业中，提取骨架曲线可使动画角色在骨架的的控制下完成多种复杂的运动；在海量三维模型库中搜索时，利用对三维模型的骨架提取，提供低维特征，可快速查找到自己感兴趣的模型。

此外，曲线骨架还可以用于形状分析、表面重建、动作规划等其他方面，其原理类似三维搜索中给模型生成低维特征。

1．2 现有的骨架提取技术

近年来，针对从三维模型中提取曲线骨架的方法层出不穷。总体来说，这些方法根据处理输入模型的不同，可以分为2大类型：

1）处理三维网格或体模型 如基于拓扑细化技术［2］、基于距离矩阵和基于Reeb图思想，其中著名的有Hilaga等提出的MRG［3］以及基于模型分解［4］等方法。

2）处理点云数据 由于点云数据没有显式的拓扑连接关系，以及部分数据可能缺失，导致该问题更有挑战性。目前基于点云的提取曲线骨架的方法假设数据有不同的特性，因而并不能处理通用模型。

2 从不完全点云提取三维柱状模型曲线骨架

笔者研究的骨架提取算法基于旋转对称轴ROSA［5］，该算法要求被处理图像大体结构上是圆柱形的，如图1（a）所示。利用平滑切割的迭代算法来计算点云的旋转对称轴，然后对非圆柱形连接区域进行特殊处理，这样可以获得有中心的、拓扑简洁并且完整的一维骨架 （见图1）。这种方法主要用来从大体上是圆柱形的形状中提取骨架，甚至可以从丢失了大量重要数据的形状中提取到骨架。

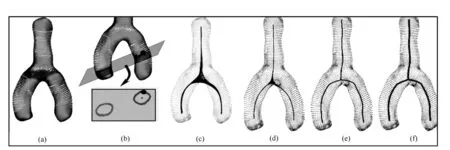
图1 基于旋转对称轴ROSA的骨架提取算法

2．1 切割平面

柱状模型的旋转对称轴上每一点相当于一条狭窄的近似平滑的 “带”状形，如图1（b）所示。这促使把平滑切割应用在输入点云中，用来局部化搜索形状骨架上的旋转对称轴点。显然，并不是所有的切割平面都隐含适合的旋转对称性。搜索最佳的切割平面，同时锚定在输入点云中的每一个样点的搜索。锚定搜索有3个好处：在旋转对称轴创建时，锚点能产生对切割平面附近的相关样本集的搜索；锚定切割平面也就意味着点云和计算骨架的自然对应；锚定搜索可以促使快速搜索最佳切割平面。

2．2 旋转对称轴的创建

取代同时优化旋转对称轴点的方向和位置，为了实现更高维次的搜索，笔者采取分离这2个组成部分的方法：先优化方向然后定位，这样每个问题均成为线性问题，可以闭合形式解决。特别是通过点云中的每个样点，可以找到最佳切割平面，其常规点能最小化与切割平面相近的有关点集的角度差异；通过不断迭代找到最佳方向。一旦找到最佳切割平面，基于相关有向点集可计算出旋转对称轴点的最佳位置。

2．3 旋转对称轴与中轴的关联

图2（d）显示，在二维空间中建立旋转对称轴，与中轴［6］有密切联系。事实上，如果迭代趋同，简单几何变量显示最佳旋转对称轴点就在形状边缘的双切圆的中心位置。如果双切圆在形状的内部，那么这点即位于中轴上。考虑到不限制双切圆在形状内部，旋转对称轴点一般属于边界曲线的对称点集，边界曲线也就是双切圆的的中心点的轨迹。如果把点的方向也加入考虑，旋转对称轴点集比完全对称点集的条件更受限制。迭代旋转对称轴的创建和与中轴关联的二维图示如图2所示。

2．4 关节处理及曲线骨架提取

模型的关节处一般不是圆柱形，因而没有简单的旋转对称轴。笔者利用点云和骨架之间的空间相干性来保证骨架结构上的点能提供分支旋转对称轴的平滑连接。由于这一步不强制关节处的结构是一维的或者刚刚好在中心位置，可以利用细化和中心定位法进行后加工。细化程序利用一维最小二乘移动法来创建，这就允许对关节和分支进行有区别的处理，见图1（d）。结果骨架曲线上的点根据分枝的旋转对称轴来确定中心，并且要和关节点的唯一中心一致，这样才能和附近的分支连接起来。作为结果的结构，要十分接近一维，并能容易地转化成曲线段集合，如图1（f）所示。

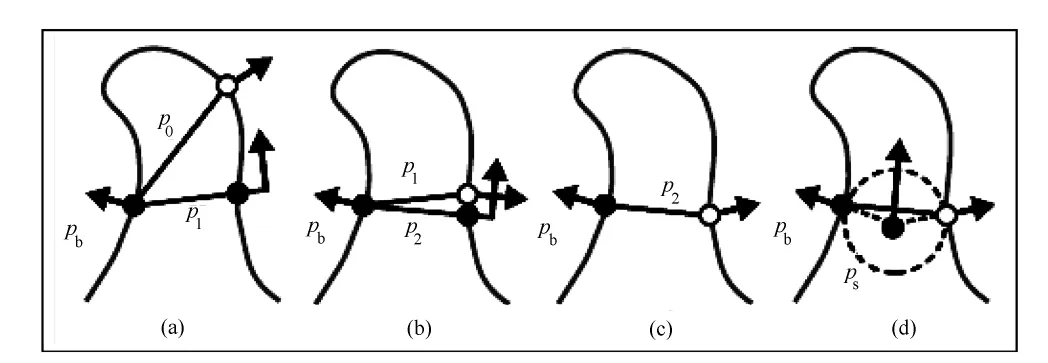
图2 迭代旋转对称轴的创建和与中轴关联的二维图示

3 结 语

针对带关节的大体为圆柱体的形状，在现实扫描或者实时捕获时，会得到包含大量空洞或者严重走样的不完全点云数据。为理解形状和方便控制图形，需要有一种健壮的方法从不完全点云中提取曲线骨架。基于这种想法，笔者提出了基于旋转对称轴从不完全点云中提取曲线骨架的算法。该算法计算出的曲线骨架是完整的，除了隐含的不完整数据源，它保证是和输入点云有关联的一维结构。

针对现有方法不能处理通用模型的现况，未来研究方向可以增加人机交互功能［7］，用户只需要在屏幕上粗略勾画，程序会计算对应的曲线骨架结点位置，并判断这些骨架节点之间的连接关系。后续工作需要解决的关键技术主要包括以下几点：①骨架提取算法的研究。针对不同表示形式的三维模型，选择最佳的曲线骨架提取算法。②骨架结点位置的定位。用户勾画，选取最佳算法，得到正确的骨架结点。③确立骨架结点间的连接关系，并能任意增删骨架结点或者骨骼。

［1］Blum H．A transformation for extracting new descriptors of shape Models for the perception of speech and visual form ［M］ ．MIT Press，1967：362-380．

［2］Tierny J，Vandeborre J P，Danudi M．3Dmesh skeleton extraction using topological and geometrical analyses［A］．In：Proceedings of Pacific Conference［C］．Taipei，2006：85-94．

［3］Hilaga M，Shinagawa Y，Kohmura T，et al．Topology matching for fully automatic similarity estimation of 3Dshapes［A］．In Proc．of SIGGRAPH ［C］．2001：203-212．

［4］Lien J M，Keyser J，Amato N M．Simultaneous shape decomposition and skeletonization ［A］．Proceedings of the 2006ACM symposium on Solid and physical modeling ［C］．2006：219-228．

［5］Tagliasacchi A，Hao Zhang，Cohen-Or D．Curve skeleton extraction from incomplete point cloud ［J］．ACM Transactions on Graph，2009，28 （3）：71．

［6］Bouix S，Siddiqi K，Tannenbaum A，et al．Medial axis computation and evolution ［M］．Statistics and Analysis of Shapes，2006．

［7］孙正兴，冯桂焕，周若鸿 ．基于草图的人机交互技术研究进展 ［J］．计算机辅助设计与图形学学报，2005，17（9）：1889-1899．