复合控制模式的长行程纳米定位控制系统
张晴,王呐,周浩
(合肥工业大学仪器科学与光电工程学院,安徽合肥230009)
0 引言
纳米定位平台是微纳米三坐标测量机的重要组成部分,为准确定位,本文使用基于BPNN-PID(误差反向传播神经网络PID)的控制器来控制平台精准定位至纳米级。
传统X-Y 平台通常是由两个单轴移动平台堆叠而成,由于轴与轴之间互相干扰即使单轴具有纳米级定位精度,也很难使系统同样具有纳米级定位精度,为此采用符合三维坐标阿贝原则的共平面平台[1],理论上可完全消除阿贝误差。
作为闭环定位控制系统中的平台驱动部分,需选用具有长行程兼高分辨力的驱动器。超音波马达具有结构紧凑且将多种驱动模式整合到一个驱动器中的优点,本文采用以色列Nanomotion 公司的超声波马达[2]。其使用侧面摩擦力作为驱动力的机制使得平台运动稳定性对导轨摩擦力变化非常敏感,因而对其控制是一大难点。传统使用固定参数的PID 控制器不能克服摩擦力变化带来的速度振荡,需用自适应性的PID[3]。Zhao 使用Back Propagation(BP)模糊神经网络控制超音波马达速度,但只给出了仿真结果[4];Seniyu 提出使用BPNN 算法控制超音波马达速度,但是没有实际应用[5]。本文使用BPNN-PID(Back-Propagation Neural Network PID)来控制以HR4 及AB2[2]驱动的平台,以实验室自行开发的多自由度传感器MDFS(Multi Degrees of Freedom Sensor)作为长行程纳米定位控制系统中的位移反馈。平台用在微纳米三坐标测量机中,快速逼近目标时的驱动速度限制在1 mm/s,此连续运动使用马达的AC 模式,同时使用BPNN-PID 控制速度。微米级行程使用马达的Gate 模式,由于Gate 模式是离散的小步驱动,只需使用简单的比例PID 来控制步长。最后使用DC 模式做精确的位移调整,此时重新使用BPNN-PID 来控制,与AC 模式不同的是此时的控制量是位移,通过BPNN-PID 调整驱动电压以抵抗应力释放和压电陶瓷元件的蠕变效应,从而锁定平台的位置。
1 纳米定位控制系统组成与结构
该运动控制系统由激励系统(两个超音波马达),位移量测系统(两个多自由度传感器MDFS)和自调式神经网络PID 构成。编程环境使用Borland C++ Builder 6.0,输入输出信号经由NI(National Instrument Co.)公司PCI 系列采集卡进行A/D,D/A 转换,图1 为控制系统原理图。

图1 基于BP 神经网络的二维共平面平台控制系统原理图
单颗压电陶瓷(PZT)元件的原理如图2(a)所示:在PZT 上表面置有四个电极A,B,C,D,每个电极为PZT 约四分之一的上表面积,而PZT 的下表面覆盖单一电极,斜对角线的电极(A 和C,B 和D)由导线相互连接。激励电压使得两组电极一组伸长,一组缩短时,将使PZT 元件产生弯曲模态运动,而两组同时伸长或缩短时,则产生伸长模态。将与PZT 元件共振频率相同的39.6 kHz 的电压作用在其上时,会激发PZT 元件同时产生弯曲与伸长模态的运动,此两种状态合成为一椭圆形运动轨迹,通过PZT 元件上端的突出部分与导轨在一定预压作用下通过摩擦力驱动平台产生直线运动。若是其中一组固定,对另一组施以弦波电压时,则会往单一方向移动,由此进行方向控制。为提高马达驱动动力以增加稳定性及保持力的延续性,Nanomotion 并联四颗PZT 元件组成HR4。


图2 超声波马达HR4 工作原理
HR4 马达及其驱动器AB2 提供三种驱动模式[2]。AC 模式下,HR4 驱动平台连续运动,可以看作是压电陶瓷元件无数次高频离散驱动的合成。距离目标点较远时,用此模式使平台以约1 mm/s 的速度快速逼近物体,但HR4 是通过侧面摩擦力直接驱动平台,移动平台与导轨间变化的摩擦力将影响速度稳定性,尤其平台在起动时,摩擦力特性比较复杂,速度会有过冲,需使用具有自适应性的BP 神经网络控制速度。使用AC 模式驱动平台逼近目标点至5 μm 后切换至Gate 模式,HR4 驱动平台产生20 ~50nm 的离散小步驱动,使用简单的算法对步距进行控制,只需控制步长落在DC模式可以补偿的范围内即可。Gate 模式驱动平台逼近目标点30 nm 后切换至DC 模式,补偿Gate 模式驱动结束后残留的纳米级的定位误差。该模式下,HR4 类似于传统的压电陶瓷驱动器工作,直接利用压电效应的弯曲模态。AB2 驱动器的DC 模式接受±10V 的电压按特性曲线转换为对应的微量位移。实际推动平台时,马达推动量受到导轨不恒定阻力与摩擦力的影响,推动量不再遵循理想特性曲线,需使用具有自适应性的BPNN-PID 以位移作为控制量,调整驱动电压。达到目标点后若需长时间锁位,由于压电陶瓷本身蠕变特性及机械元件应力释放,若驱动电压不变,平台会发生位移漂移,仍需使用BP 神经网络控制来调整电压以准确锁位。
为实现纳米级精度定位控制,需要高精度的传感器来作为位移反馈。该工作台中采用了迈克尔逊干涉仪加自准直仪构成的高精密多自由度量测系统MDFS[6],其中迈克尔逊干涉仪的参考光直接打在固定在平台上的的移动反射镜上,因此便可直接量测精密平台单轴移动时的移动距离与平台移动时其角度的俯仰与偏摆量,受限于相干长度,MDFS 的行程可达25 mm,分辨力优于1 nm,测量重复性精度在10 nm以内。测量结构示意图及实物图如图3所示,两轴位移感测器(MDFS)的激光器光轴处于同一高度,并交于平台中心,理论上完全符合阿贝原则。结构中,由于传感器MDFS 和超音波马达分别固定于平台两侧,马达产生的振动不会传到感测端。

图3 量测系统示意图及实物图
2 基于BP 神经网络的PID 控制原理
在本控制系统中,使用具有线性特性的PID 控制器。它根据被控量的给定值r(k)与输出值y(k)构成控制偏差e(k)=r(k)-y(k),其中AC 模式下被控量是速度,GATE 模式下是步距,DC 模式下是位移,将偏差的比例(P)、积分(I)、微分(D)通过线性组合算出下一次驱动电压。数字式PID 控制算法表达式如下式所示:

2.1 传统PID 控制
传统PID 控制使用恒定的KP,KI,KD参数,在参数的调整上需反复实验找出最佳值。如在AC 模式下控制速度时,在平台启动瞬间,摩擦力从最大静摩擦力转为滑动摩擦力,摩擦力特性比较复杂,通过不断调整PID 参数,即时是较好的控制效果也需要经历一段震荡才能进入稳态。且当现场条件改变,如导轨锁紧程度不同带来的摩擦力变化,将导致原设定的PID 参数不能再进行有效的速度控制。

图4 传统PID 调整到合理的PID 参数控速效果

图5 导轨锁紧程度改变时,原先的PID 参数不再适用
2.2 基于BP 神经网络的PID 控制
为了改善上述传统PID 的不足,在本纳米定位控制系统中采用误差反向传播神经网络(BPNN)来实时调整PID 控制参数。BP 神经网络的具体算法参考文献[5-6]。

图6 BP 神经网络结构
图6所示为BP 神经网络的结构,通过BPNN 算法,将被控量偏差e(k)作为学习量,来自动调整PID控制器的三个参数Kp,Ki,Kd。它由输入层、隐藏层、输出层组成。输入层三个神经元的输入分别为e(k),∑e(k)及e(k)-e(k-1),对于隐藏层和输出层来说,每个神经原j 的输入netjn和输出yjn如公式(2)所示[7]。

式中:θj是各神经原的阈值;ωij是前一层到后一层的连接权。输出层中三个神经原的输出量即为PID 控制器的比例系数Kp、积分系数Ki、微分系数Kd。
BPNN 实时修正输入层到隐含层以及隐含层到输出层之间的连接权ωij,算法依据为使用最快速度下降(最速下降法)以使其指标函数最小化。

3 实验
为验证以上BPNN-PID 控制系统的性能,设计如下两部分实验。
首先,假设MDFS 的测量精度准确可靠,验证AC 模式下控速和DC 模式下准确定位。图7 为BP 神经网络控制效果,实验表明在AC 模式下控速时,BP 神经网络可成功消除平台起动时的速度过冲,并能在全行程中保持稳速运动。用Gate 模式的步进运动来过渡到DC 模式可调整的距离。图7(b)显示在Gate 模式控制结束后,DC 模式驱动可以迅速让平台进入稳态(约0.2 s)
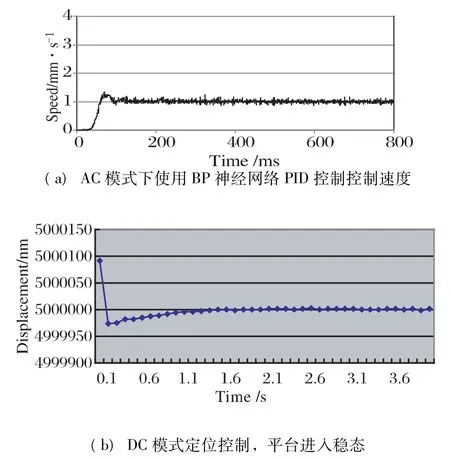
图7 BP 神经网络控制效果
其次,验证MDFS 作为位移反馈时整个系统定位控制的精度,以SIOS SP-2000 激光干涉仪作为标准,当平台运动到设定的位置后,读取MDFS 和SIOS 读值,两者之差即为定位误差,多次重复可得定位误差的重复性。进行单轴比对时的系统结构图如图8所示。由于MDFS 的测量线和SIOS 激光干涉仪的测量线并不平行,且导轨非理想直线,因此先对5,10,15 mm 三点进行试验,所得误差进行三次多项式拟合,获得一修正函数,曲线如图9所示。

图8 使用激光干涉仪校正MDFS 精度

图9 误差修正曲线
然后将经过激光干涉仪校正后的MDFS 作为定位控制系统的位移反馈,分别对1,5,10,15 mm 四个位置进行定位控制,在驱动之前用修正函数计算出修正量对目标位置点进行补偿,每点重复5 次,定位控制效果如表1所示,其中ωn为定位误差的极限偏差。

表1 不同行程的定位误差
4 总结
本文介绍了一种使用BPNN-PID 控制复合运动模式下的长行程纳米定位系统。针对马达HR4 及其驱动器AB2 提供的三种驱动模式,分别以速度、步距、位移作为控制量,通过使用不同的控制策略达到纳米级定位精度。控制系统具有良好的稳定性及抗干扰能力,使用经SIOS SP-2000 激光干涉仪校准并补偿定位误差后的MDFS 作为位移反馈,补偿后在20 mm 的行程内定位误差极差小于15 nm,标准差小于5 nm。结果证明此平台定位控制系统可用于微纳米三坐标测量机上。
[1]苗晋伟.纳米三坐标测量机探头研制与系统整合[D].合肥:合肥工业大学,2012.
[2]Nanomotion Ltd.AB2 driver user manual[D].D/N:AB02458000-00 REV.C.2011.
[3]程方.纳米三坐标测量机测控系统关键技术研究[D].合肥:合肥工业大学,2010.
[4]Zhao X,Chen W,Shi S.Ultrasonic motor's velocity control based on the BP fuzzy neural network with stored information.[C]// proceedings of 1st International Symposium on Systems and Control in Aerospace and Astronautics.2006:1137-1140.
[5]Senjyu T,Miyazato H,Yokoda S,et al.Speed control of ultrasonic motors using neutral network[J].IEEE Trans.Power Electron,1998,13:381-7.
[6]林仲豪.微型三次元量测仪之结构改良与自校正方法之研究[D].台湾:台湾大学机械工程研究所,2012.
[5]Sirisena H,Teng F.Multivariable pole-zero placement self-tuning controller[J].International Journal of Systems Science,1986,17:345-352.
[6]He S Z,Tan S H,Xu F L,et al.,Fuzzy self-tuning of PID controllers[J].Fuzzy Sets and Systems,1993,56:37-46.
[7]Wang J,Kang L Y,Cao B G.Neural network PID control of a distributed power generation system based on renewable energy[J].Journal of Applied Sciences,2005,5(10):1772-1776.

