大尺寸坐标测量技术在大型部件装配应用中的若干问题
马骊群,曹铁泽,王继虎,孙安斌
(中航工业北京长城计量测试技术研究所,北京100095)
0 引言
大部件的生产需要强大的计量手段支撑,除了使用传统的工装卡具定位方法对产品进行检测外,也越来越多地使用便携灵活的大尺寸空间坐标计量设备对产品装配过程进行质量控制[1]。这些基于空间坐标的计量设备通过获取产品的坐标信息来实现对产品质量的评定[2-4]。
激光跟踪仪、激光雷达、摄影系统、结构光视觉系统、室内GPS 系统等便携式大尺寸空间坐标计量设备及技术尽管各有特点,但依然是通用设备和检测技术,能够在一般的环境条件下满足大多数零部件的常规测量,但在非常规状态下,通用的测量方案无法满足要求[5-7]。本文针对大部件装配中遇到的几个重点问题进行讨论。
1 关于复杂曲面的评价
在航空、电力、汽车制造领域,带有复杂曲面的大型部件的装配与加工任务越来越多,采用这类大型结构件可以有效地改善产品的性能、缩短装配周期、减少重复劳动并降低成本[8]。然而由于核心设计中缺乏基于测量的设计,在进行复杂曲面装配时基于最佳拟合的曲面评价方法无法满足装配定位的要求。主要原因在于曲面的偏差是产品的主要参数,决定产品的性能;但装配测量时依赖的是对曲面上具有特殊的结构特征,如定位线、定位孔、定位面等的控制,这些特征用于将带有曲面的大部件与其它部件之间的定位与连接。最佳拟合的曲面评价方法可以使曲面形貌偏差最小,却无法保证结构特征的偏差能否满足装配需求[9-10]。如何保证连接后的整体结构依然保持部件加工后的曲面形貌,即结构特征与型面的一致性,就成为复杂曲面评价的关键问题。
1.1 复杂曲面评价的一般方法
在大多数的计量分析软件中,关于复杂曲面评价的一般方法有两种:
1)型面自由拟合法。该方法将型面测量数据与CAD 数模对准,利用最小二乘拟合算法,得到与CAD型面偏差最小的部件曲面状态。
2)特征点拟合法。依靠部件特征将部件与CAD数模对准,利用最小二乘拟合算法使曲面特征点与CAD 模型上的特征点的偏差最小,以此为基准检查曲面测量值与CAD 型面的偏差。
这两种方法各有利弊,第一种方法所得到的曲面与实际加工结果吻合,但曲面的结构特征通常具有较大的偏差。第二种方法尽管特征偏差很小,但通常得到的曲面与实际加工结果偏离较大。
1.2 有效的评价方法
考虑到一般方法的特点,可以将两种方法结合起来,即采用特征约束下的型面拟合法,使评价结果更接近部件本身的真实状态。下面以飞机机翼蒙皮成型模评价过程为例,说明这种评价方法的处理方案。
飞机机翼蒙皮复合材料组合成型模具是为了制作材质是复合材料的飞机机翼蒙皮,它包括机翼蒙皮成型模、机翼蒙皮肋板固化模等,见图1。加工蒙皮时固化模的型面必须与成型模的型面完全对准,然而对准固化模依赖于固化模上的特征点,因此固化模的特征与型面必须严格一致。

图1 复合材料组合成型模具
为了评价固化模能否满足装配需求,可采用下面的处理方案:
1)测量曲面点与特征点;
2)提取特征点,将部件与CAD 数模对准;
3)在特征对准的基础上,检查型面偏差是否满足要求,满足要求则产品合格,不满足进行曲面最佳拟合;
4)剔除离群值,判断最佳拟合后的型面偏差是否满足要求,不满足则产品不合格;
5)对于最佳拟合合格的曲面,检查特征点在曲面最佳拟合坐标系下的偏差是否满足要求,满足要求则产品合格;
6)若特征不满足要求,则在曲面拟合的基础上,增加特征点约束,重新进行曲面与特征的最佳拟合,判断型面偏差与特征偏差是否满足要求,若同时满足要求产品合格,若不满足则需要重新加工特征或修正曲面。
表1、表2 给出了靶标特征拟合、型面自由拟合、靶标约束下型面拟合三种情况下的型面偏差分析结果和特征点偏差的评价结果。其中,在型面上选取的总采样点数为2189 个,要求型面偏差RMS≤0.15 mm,靶标点最大偏差不超过0.5 mm。

表1 不同评价方法下的型面偏差

表2 不同评价方法下的特征点偏差 mm
从表1、表2 可以看出:在靶标特征拟合下,型面偏差RMS=0.24 mm,不满足要求,靶标点最大偏差0.45 mm,满足要求;在型面自由拟合下,型面偏差RMS=0.11 mm,满足要求,靶标点最大偏差0.68 mm,不满足要求;当采用靶标点和型面共同拟合时,型面偏差RMS=0.13 mm,靶标点最大偏差0.50 mm,均满足要求,产品合格。
2 关于统一空间测量网(USMN)
通常计量设备的测量范围决定了可测工件的最大尺寸,但计量设备的测量不确定度通常与测量设备的范围直接相关,测量范围越大测量不确定度越大。以激光跟踪仪为例,空间坐标测量不确定度约在(15 +6L)μm,测量范围可达几十米,若使用单台仪器完成一个长40 m 的大部件测量,则近设备端目标点测量不确定度远小于远设备端目标点测量不确定度。如何在扩大测量范围的同时又可将测量不确定度限制在一定范围内,是大部件装配(如飞机总装)中最常遇到的问题。解决这一问题的有效方法是创建统一空间测量网(简称USMN)。
2.1 USMN 技术
USMN 技术[11]是一种由多个(种)测量设备构建的空间坐标测量网,它通过足够数量的固定参考点将多个计量设备联系起来并统一在一个坐标系下。所构建的测量网的测量不确定度具有测量设备本身的特征,体现出测量设备的性能并与测量设备的测量要素相关联;与此同时被赋值的固定参考点具有确定的不确定度场,不确定度具有各测量设备测量不确定度分量的优势。
以球坐标系的测量设备为例,如激光跟踪仪、全战仪等,测量要素为距离l、水平角θ、俯仰角φ,设备的坐标测量分量为[12]m=(l,θ,φ),USMN 的构建过程如下:
1)建立由坐标未知的固定点构建的测量场,各站逐次测量固定点,测量点pik可描述为
pik=f(mki,uk)
式中:mki为各测站相应测点的坐标分量;uk为测站的不确定度;i 为测点号;k 为测站号。
2)求出固定点坐标pi,使残差最小。
仪器的坐标转换矩阵令tk=[Bx,By,Bz,Rγ,Rβ,Rα]k,寻找tk(k=1,2,…,m)使转换误差最小,其中Ek=[εk]为每站的转换误差。
4)根据残余误差确定不确定度分量,将残差按坐标分量进行分组:
rl=[E 中的所有εl]
rθ=[E 中的所有εθ]
rφ=[E 中的所有εφ]
进行不确定度分量A 类评定[13-14],有

得到测量网的不确定度结果Ul,Uθ,Uφ。
2.2 USMN 的优势
1)USMN 测量不确定度的传播小于转站测量
转站测量也是一种扩大测量空间的测量方式,但转站测量中公共点是由已经存在的测量站来赋值的,所赋的值具有所测站的不确定度水平,增加的测站除了设备本身的不确定度外还继承了公共点的测量不确定度,图2 给出了各公共点不确定度的空间,可以看出随着测站的增加不确定度空间也在增加。
在USMN 测量中,固定目标点的赋值是由该点的所有测站所决定,每个坐标点的不确定度会根据参与测量的各测站的不确定度得到均化,图3 给出了各公共点不确定度的空间,与图2 比,不确定度的传播远小于转站测量。

图2 转站测量不确定度的传播

图3 USMN 测量不确定度的传播
2)坐标点不确定度场具有测量设备不确定度分量的优势
对于可被多个测站观测到的空间坐标点而言,测量不确定度体现出各测量设备测量不确定度分量的优势,坐标点的不确定度场得到改善,见图4,改善程度与测量不确定度分量的权值相关。
3 关于装配调整过程中的回归控制
3.1 回归控制的必要性

图4 坐标点的测量不确定度场
在大部件的装配测量中最难把控的是设定测量回归点。测量回归点是保证测量设备尽管受到测量环境影响依然能回归到初始设定的状态下的控制点。对于几个小时的装配测量周期而言,环境变化较小,回归点的作用较小,但很多大型部件的装配调整所需要的时间周期都很长,少则几天,多则数月,整个调整测量过程存在诸多不可控制的因素,如:①参考基准的改变;②设备基础的变化;③室内环境的波动;④室外环境的影响。
这些因素导致仅依赖长期测量回归点来实现对测量设备的回归控制的方案无法满足部件预期的装配精度要求。
3.2 长期测量过程中的回归控制方法
若要实现对测量设备的回归控制,首先要观测回归点相对于环境的变化规律。通过观测不同时间段设备基础回归点、装配部件回归点随测试现场内、外环境的变化规律,根据变化规律将装配调整过程分解,确定每个分解过程的调整目标,逐步达到最终的预期调整目标。下面以大型紧缩场反射面的拼接装配调整为例,说明回归控制方法。
某大型紧缩场的反射面是由30 块面板组块构成(见图5),每块面板尺寸约2 m×3 m,都要安装到面板支撑背架上,要求通过调整机构将30 块面板拼成一个完整的反射面。

图5 大型紧缩场反射面的安装调整
调整测量可采用激光跟踪仪。受环境的影响跟踪仪相对于面板背架、背架地基等产生不同程度的位置变化,这些变化幅度超出了反射面的拼装精度要求。为此采取如下措施:
1)在全场设置回归参考点,这些参考点的位置是固定的,分别位于安装支架上、地面基础上和建筑墙体上(见图5)。
2)检查回归点的长期位置变化量,通过每日多次观测,连续多天重复观测(3 ~5 天),获得回归点长期变化量,变化量见表3。
3)检查回归点的每日位置变化量,选择不同的室外天气状况,晴天、阴雨天要分别观测,每日多次观测,获得参考点单日变化量。
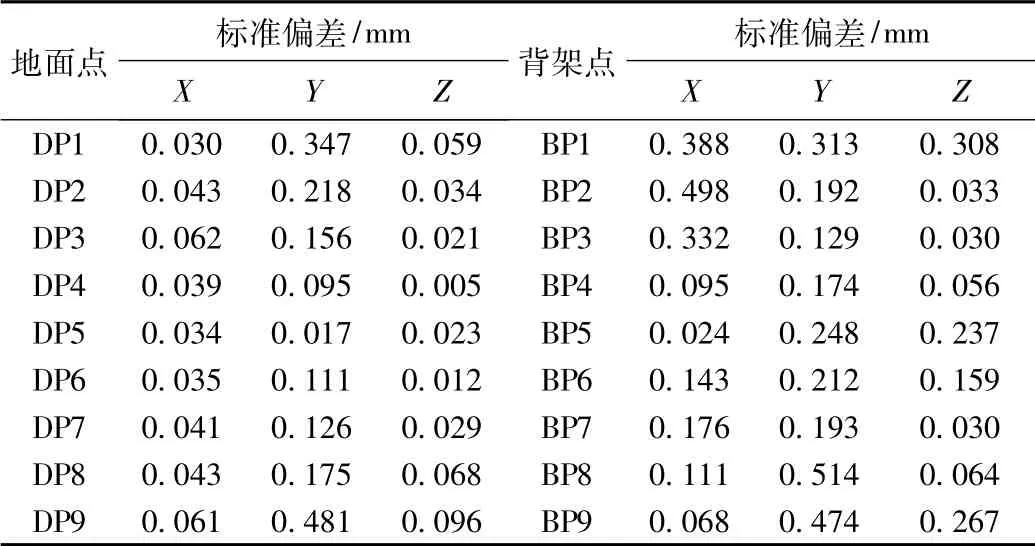
表3 回归点长期变化量
4)检查面板回归点每日相对位置变化量(见表4)。

表4 面板回归点每日变化量
5)根据回归点变化规律,对调整进行阶段划分,并确定调整目标(见图6)。

图6 回归点变化规律与调整目标
6)按照调整目标进行调整,各个阶段的调整结果见图7,其中图7(a)为在无测量误差的情况下所能达到的理想装调精度。

图7 各个阶段的调整结果
4 结论
测量设备良好的通用性给大多数的测量任务提供了有效的解决方案,但绝大多数测量设备都存在一个共性问题:测量范围越大测量精度越低、测量周期越短测量稳定性越高。大部件装配测量任务的特点是大尺寸、高精度、长周期,针对这一特点本文给出了大型复杂曲面的评价方案、大尺寸空间坐标测量网的建设方案和大型部件装配过程中的测量回归控制方案,这些方案与常规的解决方案不同,但可以使用通用测量设备来实现。方案具有可操作性和有效性,通过进一步深度分析和验证,有望成为未来解决大尺寸测试技术中同类问题的通用方案。
上述所讨论的问题都是为了提高大部件的装配精度。考虑到任何装配任务都有它的独特性,因此在使用这些方法时需要注意以下事项:
1)评价大型复杂曲面之前,应将工件状态调整到加工状态;评价曲面时,应适当加大用于装配的特征权重,减小用于测量的特征权重。
2)USMN 是一种基于固定点的组网方式,固定点的稳定性决定了设备的稳定性,这就意味着设备固有的稳定性不再是整个测量网稳定性的唯一保障,因此固定点的设置非常重要。
3)在长期装调测量中,回归控制需要监控的目标有测量场室内外环境变化,其中室内要注意温度、气流、温度梯度等变化,室外要注意天气、光照、震动、地下水等的变化;测量场基础位置漂移,包括设备基础、固定监控点、工件基础的不同时间段的漂移;测量场的线性补偿,包括对工件材料线性补偿、对设备空气折射率补偿等。
[1]马骊群,王立鼎,靳书元,等.工业大尺寸测量仪器的溯源现状及发展趋势[J].计测技术,2006,26(6):1-5.
[2]Cai B,Guo Y,Jamshidi J,at al.Measurability Analysis Of Large Volume Metrology Process Model For Early Design[C]// Proceedings of the 5th CIRP International Conference on Digital Enterprise Technology.France,Nantes:CIRP,2008.
[3]Muelaner J E.Maropoulos P G.Large Scale Metrology in Aerospace Assembly[C]// Proceedings of the 5th CIRP International Conference on Digital Enterprise Technology.France,Nantes:CIRP,2008.
[4]ISO 10360-2 Geometric Product Specifications Acceptance and Reverification Tests for Coordinate Measuring Machines- Part 2,CMMs used for measuring size[S].2002.
[5]马骊群,曹铁泽,王继虎,等.便携式坐标测量系统在航空发动机关键部件检测中的应用[J].计测技术,2008,28(6):9-12.
[6]Estler W T,Edmundson K L,Peggs G N,at al.Large-scale metrology-An update[J].CIRP Annals-Manufacturing Technology,2002,51(2):587-609.
[7]Peggs G N,Maropoulos P G,Hughes E B,at al.Recent developments in large-scale dimensional metrology[J].Pro.IM E B J.Eng.Manufacture,2009,223(B6):571-595.
[8]Muelaner J E,Cai B,Maropoulos P G.Large Volume Metrology Instrument Selection and Measurability Analysis[C]// Proceedings of the 6th CIRP-Sponsored International Conference on Digital Enterprise Technology.Hong Kong:CIRP,2009.
[9]Saadat M,Cretin C.Measurement systems for large aerospace components[J].Assembly automation,2002,22(3):199-206.
[10]Maisano D A,Jamshidi J,Franceschini F,at al.Indoor GPS:System Functionality and Initial Performance Evaluation[J].International Journal of Manufacturing Research,2008,3(3):335-349.
[11]New River Kinematics.Spatial Analyzer User's Manual[Z].2007.
[12]NIST.ASMEB 89.4.19-2006.Performance Evaluation of Laser-Based Spherical Coordinate Measurement Systems[S].America,Gaithersburg:U.S.Department of Commerce,2006.
[13]BSI.PD 6461-3:1995 General Metrology- Part 3:Guide to the expression of uncertainty in measurement(GUM)[S/OL].[2013- 03- 16].http://www.docin.com/p-295902009.html.
[14]Cox M G,Forbes A B,Flowers J L at al.Least Squares Adjustment in the Presence of Discrepant Data[M]// Ciarlini P.Advanced Mathematical & Computational Tools in Metrology VI.Singapore:World Scientific,2004:37-51.

