GPS 高程拟合模型在工程勘测中的应用研究

杨新国

(中铁第一勘察设计院集团有限公司，陕西 西安 710053)

1 GPS水准高程的原理

由于GPS高程所表示的是大地高h，但是我国高程系统采用的高程是正高H正高或者是正常高H正常高，这就需要两者之间进行转换得到我们所需要的高程值。

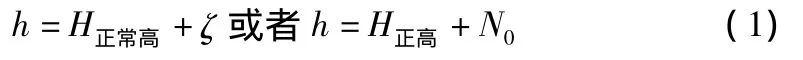
上式是大地高与正常高、大地高与正高之间的转换关系，其中，ζ为高程异常值;N0为大地水准面之间的差距。

2 GPS水准拟合常用的方法

目前在区域较小或者平坦的区域内，GPS拟合的精度有所提高，能够满足工程一定精度的需要，但是还是要比相应等级的水准测量精度要低很多，如果要更加精确的得到高区域各GPS点的正高或者是正常高，那就必须获得各点的大地水准面的差距值和各点的高程异常值。

求得各点的高程异常值，经GPS测量得到各点的大地高，那么就可以根据式(1)求得各点的正常高。

目前外业测量所常见的方法有以下几种:

1)GPS测量与水准测量相结合;2)短距离三角高程测量和GPS相结合;3)经纬仪测量和GPS相结合;4)重力测量与水准测量相结合。

后三种方法由于受仪器设备、观测条件、已有数据资料、精度等因素的限制在实际测量工作中很难使用，而第一种方法，由于只需在GPS点上再测一定数量的水准高程就可求解，因此在实际测量工作中应用最为广泛。

3 GPS水准拟合的模型

截止到现在，用于计算高程异常拟合的数学模型很多，归纳起来有以下三种拟合模型:平面拟合模型、曲面拟合模型和常数拟合模型。

各个模型有各个模型的特点，我们可以利用各个模型的特点为我们在工程测量中解决各种问题，以上三种模型可以根据实际的地理地形情况选择合适的模型为我们服务，从而满足工程高程测量的精度要求。

3.1 平面拟合模型(平面拟合法)

如果我们所需的控制点在范围较小或者地形起伏不大的范围内，我们就可以认为该区域的似大地水准面等同于或者近似于平面。

假设控制区域内公共点的高程异常和各个点之间的坐标有如下的关系:

或者为 ζi=a1+a2B+a3L。

其中，a1，a2，a3均为模型参数。

如果公共点的数目大于3个，则可以列出相应的误差方程为:

平面拟合模型所需要的公共点的个数一般大于3个，根据文献记载，该方法在120 km2平原地区，拟合精度可达3 cm～4 cm。

3.2 曲面拟合模型(二次曲面拟合法)

在某些区域由于地理或者地形条件变化突出，在该区域内高差变化较大引起大地水准面变化不规则，那么采用平面拟合模型会引起较大的测量误差，达不到所要求的测量精度，不能满足工程设计或施工需要，这样我们就采用曲面拟合法对该区域进行曲面拟合达到我们所需要的精度，曲面拟合法的方法也有几种，我们一般采用二次曲面拟合法，也就是在该区域内所有公共点的高程异常和各点的平面坐标之间建立相对应的关系，它们之间存在如下的数学模型:

或者 ζi=a0+a1B+a2L+a3B2+a4L2+a5BL。

其中，a0，a1，…，a5均为模型所需要求得的参数，用曲面拟合法求得该模型参数一般至少需要6个公共点或以上。当所求模型区域内公共点的个数大于6个公共点时，误差方程表示如下:

按照最小二乘法可以求得模型所需要求得的参数。

该拟合方法在丘陵地区或者高差变化较大的地区，拟合精度可优于3 cm甚至更佳。

除了二次曲面拟合法以外，还可以进一步的扩展，也就是多项式曲面拟合法，多项式曲面拟合法的数学模型为:

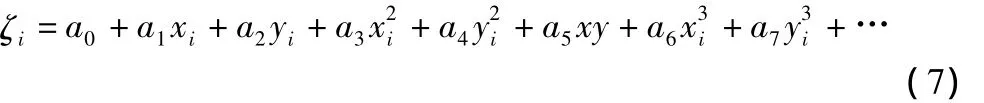
其误差方程仍然为:

其中，X为方差矩阵。

在GPS曲面拟合时，三次曲面拟合法实用性不强，随着高差变化的加大，各点的高程异常变化就会越来越复杂，计算精度也会越来越低。

当测区范围地形变化复杂但是测区面积较小时可采用的四参数拟合方法，其数学模型如下式:

3.3 常数拟合模型

常数模型拟合的基本思想是该测区内高程异常基本一致，不考虑参考椭球面与似大地水准面之间的差距变化情况，这种方法只适用于极小区域且要求该区域内似大地水准面与参考椭球面相对吻合，实际生产过程中一般不用这种方法。

4 GPS水准拟合精度评定的标准和计算方法

4.1 GPS水准拟合精度评定标准

GPS水准拟合精度评定的结果是直接影响我们使用成果的标准，所以我们从单位权中误差，内符合精度和外符合精度几方面来对GPS水准拟合精度进行检验，一般来说在控制区域内，我们一般只选择一部分已知点来求得拟合模型的几个参数，其余的已知点只是作为检核点来评定拟合曲面与区域(似)大地水准面的逼近程度。

4.2 单位权中误差的计算方法

GPS观测的是大地高，经过同步观测所得到的各点大地高差精度较高，这样给出网内某点的大地高作为起始大地高，就可以求出其他点相对于起始点的高精度的大地高，采用相应等级的联测方法联测GPS可以求得各点的正常高，根据式(1)就可以求得各点的高程异常，高程异常变化趋势平缓，可利用简单曲面进行拟合，以二次曲面拟合为例:

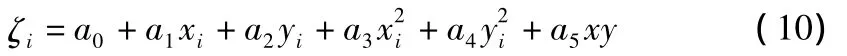
其矩阵形式为:

假设全网共布设n个GPS点，观测了m个GPS水准点(m＜n)，则拟合的误差方程式为:

设为等权观测，根据最小二乘法求得系数:

通过上式即可计算任意拟合点的高程异常值。

由误差方程可以计算拟合点残差向量V，计算单位权中误差:

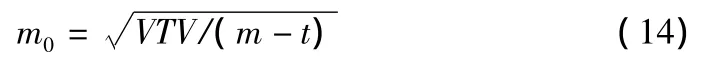
4.3 内部符合精度的计算方法

根据参与拟合计算的已知点ζi值与拟合值ζi'，用v=ζi－ζi'求拟合残差，按下式计算GPS水准拟合计算的内符合精度:

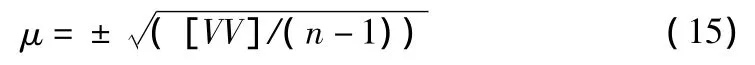
其中，n为v的个数。

4.4 外部符合精度的计算方法

根据检核点ζi值与拟合值ζi'之差，可以按下式计算GPS水准拟合计算的外符合精度:

其中，n为检核点的个数;μ，M可以近似地认为是拟合点的高程中误差。

5 实例分析

5.1 案例概况

检验段内选择了该40 km作为高程拟合区域，该区域共有21个GPS点，我们选其中11个点作为拟合的基准点(训练点)，其余点作为检验点，这11个点均匀分布于测区，且代表了测区内的高差变化情况，所采集的外业测量数据，在计算中，采用以下两种计算方法进行对比。

平面拟合整个测区。

分段采用二次曲面拟合，对于重合区域采用双三次样条函数进行重新取值。

5.2 两个模型拟合后精度比较

由表1中可以看出，曲面拟合精度较好，因为曲面拟合可以根据地形起伏情况对高程异常面进行重新组合，并对区与区之间进行光滑连接，从而使拟合曲面尽量符合实际分布。

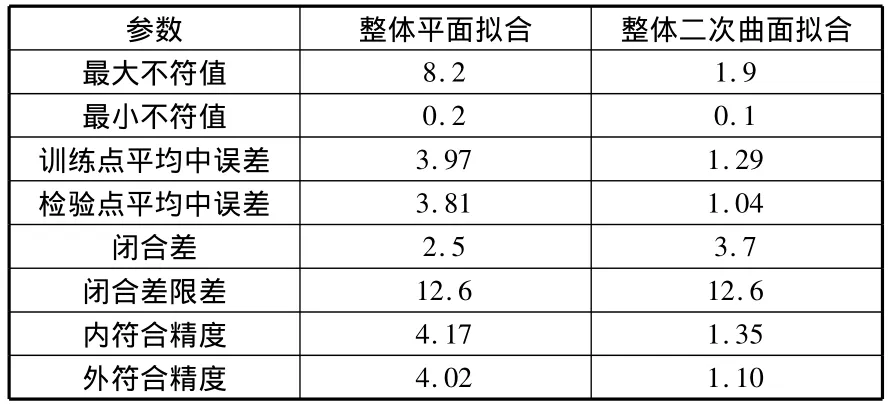
表1 拟合精度比较表 cm

6 GPS拟合精度提高的措施

GPS外业测量受到多种因素的影响导致GPS高程拟合精度的下降，所以我们必须对GPS外业的观测和GPS内业的作业来提高GPS高程的拟合精度，GPS外业观测的方法和GPS内业拟合模型的选择成为GPS拟合后精度提高的作业关键，为了这个目的，我们可以采取以下几种方法:

1)GPS外业数据采集质量的提高和外业数据采集数量的增加;

2)星历状况要良好以提高测站测定大地高精度;

3)观测条件适宜以提高联测几何水准的精度;

4)选择合适的模型以提高拟合计算的精度。

［1］张正禄.工程测量学［M］.武汉:武汉大学出版社，2002:136-155.

［2］孔祥元，郭际明，刘宗泉.大地测量学基础［M］.北京:测绘出版社，1996:89-97.

［3］徐绍辁，张华海，杨志强，等.GPS测量原理及应用(修订版)［M］.武汉:武汉大学出版社，2003.

［4］金时华.多面函数拟合转换GPS高程［J］.测绘与空间地理信息，2005(12):95-97.

［5］陶本藻，蔡凤萍.大范围GPS水准拟合模型的选取及其实验研究［J］.工程勘察，2005(1):85-89.